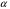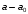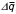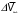|
|
ЛАБОРАТОРНАЯ РАБОТА 1 (1). Лабораторная работа 1
ЛАБОРАТОРНАЯ РАБОТА 1
ОПРЕДЕЛЕНИЕ СКОРОСТИ ВОЗДУШНОГО ПОТОКА
1.1. ЦЕЛЬ РАБОТЫ
Целью работы является практическое измерение величины скорости воздушного потока в аэродинамической трубе и оценка точности измерения. В результате выполнения лабораторной работы студенты на основе знаний теоретического материала, устройства лабораторных приборов и оборудования должны:
уметь определять скоростной напор;
уметь определять статические газодинамические переменные воздушного потока;
уметь определять полное давление;
уметь определять скорость воздушного потока.
1.2. ПОДГОТОВКА К ЛАБОРАТОРНОЙ РАБОТЕ 1.2.1. Устройство аэродинамической трубы
Экспериментальная аэродинамика - раздел аэромеханики, изучающий движение воздуха и его взаимодействие с расположенными в нем телами путем опытов, т.е. материальными методами. Для исследования такого взаимодействия обычно применяют два метода: движение тела в неподвижной среде (летный эксперимент, аэродинамическая тележка, свободное падение, ротативная машина), движение воздушной среды относительно неподвижного тела, которое является основным в аэродинамической лаборатории. Установки для создания равномерного, прямолинейного, установившегося потока воздуха или газа с заданной скоростью с целью исследования обтекания тел (моделей) называются аэродинамическими трубами. Аэродинамические трубы в основном характеризуются размерами рабочей части и максимальной скоростью потока в рабочей части. Рассмотрим устройство аэродинамической трубы УТ-1, входящей в УЛАК-1 (учебный лабораторный комплекс -1). Эта труба относится к трубам малых дозвуковых скоростей замкнутого типа с открытой рабочей частью непрерывного действия. Основные характеристики трубы: скорость потока в рабочей части, м/c рабочая часть длина рабочей части, мм выходное сечение, мм длина модели, мм мидель модели, мм2 мощность привода вентилятора, кВт число оборотов вентилятора, об/мин | 2-60 открытая 1000 600400 до 400 до1800 45 до 1300 | Аэродинамическая труба состоит из следующих частей (рис. 1.2). Формирование потока воздуха начинается в форкамере 1, которая представляет собой прямолинейный участок трубы, и предназначена для выравнивания и успокоения потока. В начале форкамеры расположен хонейкомб 2 , который представляет собой ячеистую конструкцию, состоящую из квадратных ячеек с тонкими стенками. Хонейкомб выравнивает поток по направлению, разбивая крупные вихри, а также уменьшает неравномерность распределения продольных скоростей.
За хонейкомбом установлена детурбулизирующая сетка 3, уменьшающая турбулентность потока в рабочей части трубы и неравномерность поля скоростей.
Выравнивающее действие сеток основано на большем торможении больших по величине скоростей, так как потери давления на сетке пропорциональны квад-рату скорости. Вторая сетка, установленная после рабочей части, служит для детурбулизации потока на входе в вентилятор.
Сопло 4 предназначено для разгона воздушного потока, подходящего со стороны форкамеры, до расчетной скорости в рабочей части трубы 5 и для
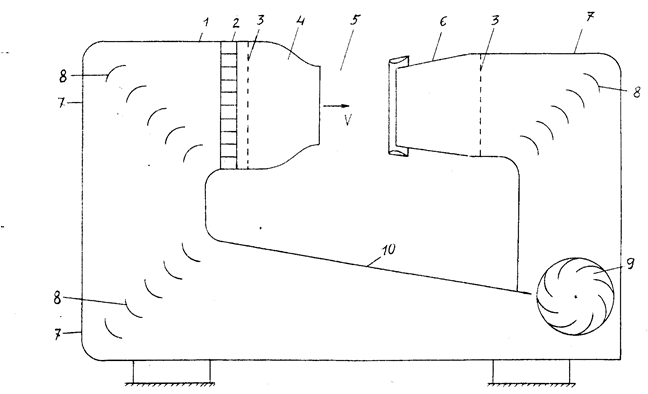
Рис. 1.2. Схема замкнутой аэродинамической трубы с открытой
рабочей частью:
1-форкамера; 2-хонейкомб; 3-детурбулизирующие сетки; 4-сопло;
5-рабочая часть; 6-двухконтурный диффузор; 7-поворотные колена;
8-повортные лопатки; 9-диаметральный вентилятор; 10-обратный канал
улучшения качества потока за счет поджатия. При поджатии скорость потока увеличивается обратно пропорционально отношению площадей сечений (следствие уравнения неразрывности). Поджатие сопла трубы УТ-1 равно 6. Все дозвуковые трубы имеют контур переменного сечения с минимальной площадью в рабочей части. Делается это по двум причинам. Во-первых, при поджатии сечения уменьшаются неравномерность поля скоростей и степень турбулентности потока, причем неравномерность поля скоростей уменьшается пропорционально квадрату отношения площадей сечений в широкой и узкой части. Для того чтобы непосредственно перед рабочей частью осуществить поджатие потока и тем самым улучшить его характеристику, необходимо после рабочей части произвести расширение потока. Во-вторых, известно, что потери полного давления по тракту пропорциональны квадрату скорости. При расширении потока за рабочей частью его скорость падает, следовательно, снижаются гидравлические потери и уменьшается потребная мощность привода и затраты энергии.
После прохождения рабочей части воздушный поток расширяется в двухконтурном диффузоре 6. Он представляет собой расширяющий канал, обеспечивающий торможение потока с наименьшими потерями и, тем самым, эффективное превращение кинетической энергии в энергию давления. В начале диффузора расположена прямоугольная профилированная поверхность, образующая второй контур, и предназначенная для отсечения и разгона струйного пограничного слоя и уменьшения градиента статического давления по длине рабочей части трубы.
В каждом из трех поворотных колен 7 установлены поворотные лопатки 8, которые служат для улучшения равномерности потока после поворотных колен и снижения гидравлических потерь. При отсутствии поворотных лопаток поток при повороте получал бы большие завихрения и был бы слишком неравномерным и турбулизированным.
Воздух в трубе приводится в движение вентилятором 9 диаметрального типа. В установившемся режиме работы трубы энергия, сообщаемая вентилятором потоку, расходуется на преодоление сопротивления воздуха при его движении по тракту трубы.
Применение диаметрального вентилятора вместо осевого позволило сократить длину трубы и исключить закручивание потока в тракте.
Обводной канал 10 служит для возврата воздушного потока и повышения его давления.
1.2.2. Проблемы определения скорости воздушного потока
При аэродинамическом способе полета летательный аппарат (ЛА) поддерживается в атмосфере за счет динамического взаимодействия с воздухом, обтекающим его поверхность.
Динамическое (или механическое, или силовое) взаимодействие при обтекании ЛА определяется распределенным воздействием на его поверхность нормальных и касательных напряжений от воздушной среды.
Под обтеканием понимается относительное движение воздуха и ЛА, то есть воздух должен двигаться относительно ЛА или наоборот, ЛА должен двигаться в неподвижном воздухе.
В теоретической и экспериментальной аэродинамике в основном используют обращенное движение, при котором неподвижный ЛА обтекается воздухом, называемым набегающим воздушным потоком или просто потоком.
Под потоком понимается воздух, частицы которого движутся преимущественно в одном направлении.
Например, воздушный поток в рабочей части аэродинамической трубы.
Значения действующих на поверхности ЛА нормальных и касательных напряжений зависят от скорости потока и в сумме создают аэродинамические силы и моменты. Очевидно, что полет ЛА возможен только при достижении определенной скорости воздушного потока (или воздушной скорости), которую необходимо измерять на борту ЛА для контроля полета.
В аэродинамическом эксперименте знание скорости необходимо для получения аэродинамических коэффициентов и критериев подобия для переноса результатов с модели на натурный объект.
Все вышесказанное подчеркивает важность знания скорости как в реальном полете, так и в аэродинамическом эксперименте.
Согласно теоретической механике скорость является кинематической характеристикой движения. Например, при равномерном поступательном движении твердого тела скорость характеризует расстояние, проходимое телом за единицу времени и определяется отношением пути ко времени. Не существует прибора непосредственно измеряющего скорость движения тел. Скорость получается расчетным путем или вручную, или автоматически с помощью прибора. Например, в автомобиле для этой цели служит спидометр.
Еще сложнее становится проблема измерения скорости воздушного потока. Здесь наибольшее распространение в практике получил пневмометрический (аэрометрический) метод, заключающийся в определении скорости по характерным газодинамическим переменным в потоке. Этот метод складывается из решения трех проблем.
Первая проблема состоит в том, каким образом получить функциональную связь скорости потока с его другими газодинамическими переменными?
Вторая проблема состоит в том, как получить в потоке нужные газодинамические переменные?
Третья проблема состоит в том, как количественно измерить эти газодинамические переменные?
1.2.3. Формула для определения скорости потока
Для решения первой проблемы: получения формулы для скорости потока нужно сформулировать так называемую научную постановку задачи.
Вывести функциональную зависимость (формулу) для определения скорости потока, используя следующие упрощающие предположения:
1. Поток предполагается идеальным.
2. Поток предполагается несжимаемым.
3. Поток предполагается установившимся (стационарным) и равномерным.
Первое предположение справедливо вне пограничного слоя и вне следа за телами, где существенно влияние вязкости. Второе предположение определяет независимость плотности воздуха от его скорости и справедливо, если число М 0,3, а скорость не превышает 103 м/с. Последнее предположение означает, что газодинамические переменные, включая и вектор скорости, во всех точках потока одинаковы и по времени не меняются.
Такая постановка задачи позволяет использовать закон сохранения энергии вдоль линии тока в идеальной сплошной среде.
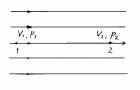
Закон сохранения энергии выражается уравнением Бернулли, которое по своему физическому смыслу записывается обязательно для двух точек потока, лежащих на одной произвольной линии тока (рис. 1.3).
|
|

| Рис. 1.3. Точки в потоке для уравнения Бернулли | Рис. 1.4. Критическая точка в потоке |
|
В этом случае уравнение Бернулли будет иметь вид:  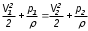
или в виде напоров  (1.1) (1.1) Уравнение (1.1) не позволяет получить зависимость для определения скорости, т.к. согласно постановке задачи превращается в тождество 0 0.
Для получения зависимости для расчета скорости нужно в одной из точек на линии тока, например, в точке 2 изменить скорость и давление, причем так,
чтобы величина скорости стала известной. Это можно сделать, если в точке 2 реализовать критическую точку. Для этого в поток надо поместить твердое тело таким образом, чтобы хотя бы часть его поверхности была нормальна скорости потока в точке 2 (рис. 1.4). Тогда линия тока в точке 2 разделится на две линии тока, которые станут огибать тело сверху и снизу.
Критической точкой на поверхности тела называется точка разветвления потока, в которой скорость течения в связанной с телом системе координат равна нулю.
Отсюда следует, что скорость  равна нулю, а давление равна нулю, а давление  возрастает и становится максимальным из всех возможных значений для данной линии тока. возрастает и становится максимальным из всех возможных значений для данной линии тока.
Процесс возрастания давления при малых скоростях происходит быстро, без значительного нагрева и без теплообмена с окружающими линиями тока и его можно принять изоэнтропическим. При изоэнтропическом процессе вся кинетическая энергия воздуха переходит без потерь в потенциальную энергию давления и наоборот.
Давление в данной критической точке обозначают  и называют полным. и называют полным.
Полным давлением называется давление изоэнтропически заторможенного газа.
Давление  обычно называют статическим давлением. обычно называют статическим давлением.
Статическим давлением называется давление в точке воздушного потока, совпадающей с положением заданной точки (например, лежащей на поверхности крыла).
Нас интересует скорость невозмущенного воздушного потока. Эта скорость будет в точке 1 в том случае, если эту точку поместить достаточно далеко от тела так, чтобы оно практически не влияло на поток. Газодинамические переменные такого потока называются переменными невозмущенного потока или потока "на бесконечности" и обозначаются  и и  . .
Физически невозмущенное статическое давление - это давление, которое действует на стенку тела, движущегося вместе с потоком.
С учетом вышесказанного, уравнение (1) принимает вид
 , (1.2) , (1.2)
где -  - скоростной напор или динамическое давление - скоростной напор или динамическое давление
Используя понятие скоростного напора формулу для расчета скорости потока можно записать в виде
 . (1.3) . (1.3)
Однако величину скоростного напора из потока непосредственно получить
невозможно. Величину скоростного напора можно определить только как разность давлений  , подставив которую в формулу (1.3) получим выражение , подставив которую в формулу (1.3) получим выражение
 = =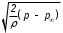 . (1.4) . (1.4)
Итак, на основании выше сформулированной научной задачи, получена формула (1.4), которая устанавливает функциональную связь скорости воздушного потока с тремя газодинамическими переменными  , ,  и и  . Очевидно, что если предположение 3 в постановке научной задачи не выполняется, то полученная формула справедлива только для одной линии тока и только в данный момент времени. . Очевидно, что если предположение 3 в постановке научной задачи не выполняется, то полученная формула справедлива только для одной линии тока и только в данный момент времени.
Из уравнений (1.3 и 1.4) видно, что задача определения скорости потока вторична по отношению к задаче определения скоростного напора. Поэтому сначала остановимся на задаче определения скоростного напора, которая, как будет показано в дальнейшем, технически проще решается.
1.2.4. Получение газодинамических переменных в потоке
Перейдем теперь к решению второй проблемы: получению необходимых газодинамических переменных. Для того, чтобы получить эти переменные нужно сначала выявить их в потоке, а затем вывести из потока в место, удобное для их измерения.
Устройства, служащие для выявления газодинамических переменных называются приемниками, например, приемник статического давления, приемник температуры торможения и т.д.
Вывод из потока и передача газодинамических переменных к месту измерения осуществляется обычно с помощью различных трубок.
Обычно в пневмометрическом методе пользуются комбинированным приемником давления, который называют насадком или трубкой Пито-Прандтля , или приемником воздушного давления (ПВД).
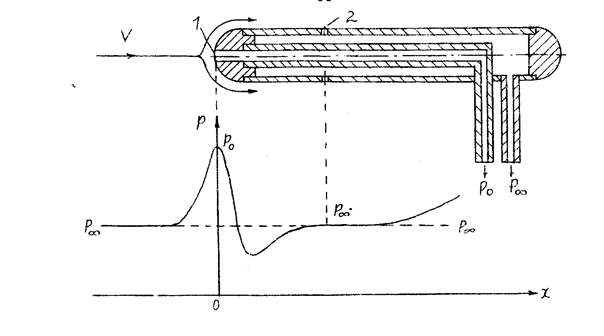
По конструкции он представляет собой две концентрические трубки, вставленные одна в другую (рис. 1.5), на этом же рисунке показано распределение давления по внешней поверхности ПВД.
Отверстие 1 служит для приема полного давления, а отверстие 2 - для приема статического давления. Полное давление обычно довольно точно воспроизводится ПВД. Точность воспроизведения статического давления сильно зависит от места расположения и размера отверстий, качества обработки поверхности и точности установки ПВД в потоке, определяемой углом атаки.
Угол атаки ПВД - это угол между его осью симметрии и вектором скорости потока.
Очевидно, что наибольшая точность обеспечивается при равенстве угла атаки нулю, чем устраняется скос потока.
Отверстия для приема статического давления обычно располагают по окружности, чтобы уменьшить влияние скоса потока вследствие неточности установки ПВД. Отверстия 2 сверлятся в том месте ПВД, где давление равно или очень близко к статическому.
Размеры ПВД должны быть, с одной стороны, как можно меньше, чтобы меньше возмущать поток, но с другой, минимальные размеры ПВД ограничиваются диаметром отверстий, слишком малые отверстия увеличивают инерционность насадка. ПВД, как любой прибор, дает нам давления с определенной точностью, определяемой его систематической погрешностью.
Систематическая погрешность складывается
- в меньшей степени из-за того, что ПВД выделяет из потока не давление торможения, а некоторое давление, осредненное по площади переднего отверстия ПВД, которое не является точкой;
- в большей степени из-за неточности определения статического давления.
Чтобы учесть эту погрешность, в формулу (1.3) вводится коэффициент  , называемый коэффициентом насадка, после чего формула принимает вид , называемый коэффициентом насадка, после чего формула принимает вид
 . (1.5) . (1.5)
Величина коэффициента  определяется при тарировке ПВД и заносится в его технический паспорт. определяется при тарировке ПВД и заносится в его технический паспорт.
Таким образом, ПВД позволяет нам выявить для использования в формулах (1.2, 1.4, 1.5) две газодинамические переменные  и и  . Третью неизвестную переменную - плотность . Третью неизвестную переменную - плотность  измерить непосредственно нельзя, такого прибора также не существует. Плотность воздуха получают расчетным путем с помощью уравнения состояния измерить непосредственно нельзя, такого прибора также не существует. Плотность воздуха получают расчетным путем с помощью уравнения состояния
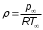 , ,
где  и и  - соответственно статическое давление и статическая абсолютная температура [K]; - соответственно статическое давление и статическая абсолютная температура [K];
 =287,05 дж/(кг К) - удельная газовая постоянная. =287,05 дж/(кг К) - удельная газовая постоянная.
Часто статическое давление в неподвижном воздухе измеряют барометрами, проградуированными в миллиметрах ртутного столба. Для перехода от мм рт. ст. к Па - единице давления в СИ необходимо воспользоваться соотношением
760 мм рт. ст. = 1,013105 Па
Измерение статической температуры является также сложной инженерной задачей, однако в лабораторных работах за статическую температуру можно принять температуру неподвижного воздуха в помещении аэродинамической трубы.
1.2.5. Измерение давления
Перейдем, наконец, к решению третьей проблемы, т.е. количественному измерению давлений  и и  . .
Для этого неизвестную величину давления надо сравнить с известным давлением. При их равенстве и определяется искомая величина давления.
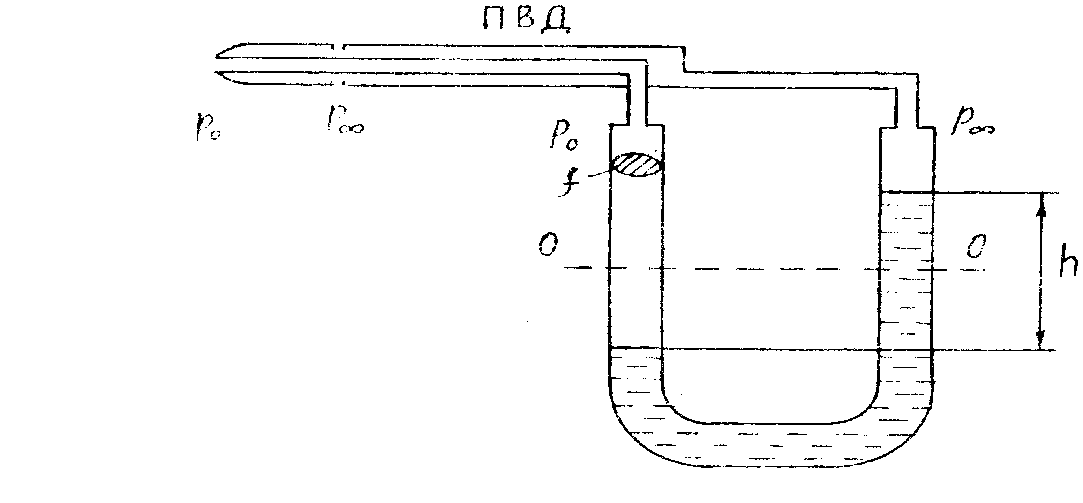 Приборы, измеряющие давление или разность давлений жидкостей и газов, называются манометрами. Приборы, измеряющие давление или разность давлений жидкостей и газов, называются манометрами.
Рис. 1.6. Двухколенный U-образный жидкостный манометр
По принципу устройства манометры бывают механические и электромеханические.
В механических манометрах измеряемое давление непосредственно сравнивается с давлением от веса столба жидкости, или с давлением от веса эталонного груза, или с давлением от сил упругих чувствительных элементов.
В электромеханических манометрах (датчиках давления) силы от измеряемого давления вызывают перемещение чувствительных элементов, которое воздействует на параметры (сопротивление, индуктивность или емкость) электрических схем. Здесь помимо датчиков требуются и соединенные с ними проводами специальные указатели.
"Классическими", наиболее распространенными и наиболее точными приборами для измерения давления являются жидкостные манометры. Однако они обладают большой инерционностью и могут использоваться только в установившихся воздушных потоках. В неустановившихся потоках, когда давление по времени изменяется очень быстро, используются датчики давления.
Из уравнений (2 и 4) видно, что нам нужно знать не абсолютные значения давлений  и и  , а только значение из разности , а только значение из разности  . Рассмотрим принцип измерения, позволяющий определить эту разность Для этой цели воспользуемся простейшим двухколенным манометром в виде U-образной прозрачной трубки, с постоянной площадью поперечного сечения (рис. 1.6). . Рассмотрим принцип измерения, позволяющий определить эту разность Для этой цели воспользуемся простейшим двухколенным манометром в виде U-образной прозрачной трубки, с постоянной площадью поперечного сечения (рис. 1.6).
Нальем в трубку жидкость с известным удельным весом  до уровня по линии ОО, который будем называть начальным положением или начальным отсчетом. Подведем от ПВД к левому колену манометра давление до уровня по линии ОО, который будем называть начальным положением или начальным отсчетом. Подведем от ПВД к левому колену манометра давление  , а к правому давление , а к правому давление  . В этом случае жидкость, сыграв роль гидравлического затвора, отклонится от начального положения и переместится в правое колено трубки, т. е. в область меньшего давления. При этом создастся столб жидкости высотой равной . В этом случае жидкость, сыграв роль гидравлического затвора, отклонится от начального положения и переместится в правое колено трубки, т. е. в область меньшего давления. При этом создастся столб жидкости высотой равной  , давление от которого уравновесит искомую разность давления. , давление от которого уравновесит искомую разность давления.
Запишем равновесие сил
 или или  . .
Замерив высоту  и умножив ее на удельный вес и умножив ее на удельный вес  , мы получаем искомую величину разности давлений, не зная их абсолютных величин. Таким образом, согласно уравнению (2) такой манометр непосредственно измеряет скоростной напор. , мы получаем искомую величину разности давлений, не зная их абсолютных величин. Таким образом, согласно уравнению (2) такой манометр непосредственно измеряет скоростной напор.
Жидкость в таком манометре выполняет три роли: "вычисляет" разность давлений, "измеряет" ее и "указывает" ее величину. Очевидно, что такой манометр может использоваться не только в аэродинамике, но и в любых технических задачах, где нужно измерить разность давлений газообразных сред.
Часто разность давлений называют перепадом давлений.
Манометр, измеряющий перепад (разность) давлений, называется дифференциальным манометром.
Дифференциальный манометр, предназначенный для измерения малых величин перепадов давления, называется микроманометром.
U-образные манометры имеют не очень удобную шкалу считывания. Значения, отсчитанные от начального положения, необходимо умножать на два. Для исключения этого, обычно в микроманометрах, одно из колен (бачок) делается со значительно большим поперечным сечением, чем другое (измерительная прозрачная трубка со шкалой). Для повышения точности отсчета измерительная трубка может изменять свой наклон. Повышение точности в этом случае заключается в более точном считывании показаний за счет увеличения пути перемещения мениска жидкости при одном и том же перепаде давления (рис. 1.7).
Для измерения перепада давления полное давление подводится к бачку, а статическое к измерительной трубке. Уравнения равновесия сил в этом случае будет иметь вид
 , (1.6) , (1.6)
где  - удельный вес жидкости; - удельный вес жидкости;
 - высота столба жидкости в измерительной трубке, измеренная от начального положения; - высота столба жидкости в измерительной трубке, измеренная от начального положения;
 - понижение уровня жидкости в бачке от начального положения. - понижение уровня жидкости в бачке от начального положения.
Величина  определяется по шкале измерительной трубки с учетом ее наклона определяется по шкале измерительной трубки с учетом ее наклона
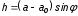 , (1.7) , (1.7)
где  - показание шкалы при измерении; - показание шкалы при измерении;
 - показание шкалы при нулевом перепаде давления; - показание шкалы при нулевом перепаде давления;
 - угол наклона измерительной трубки. - угол наклона измерительной трубки.
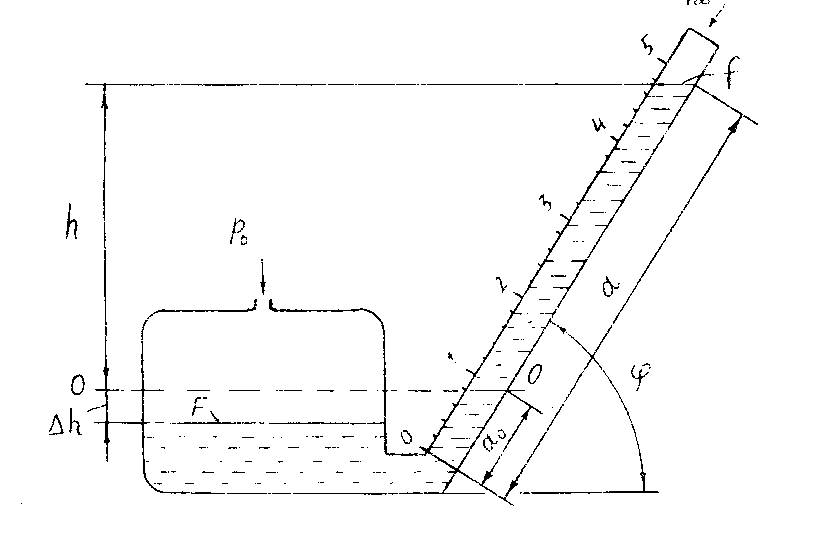
Рис. 1.7. Схема микроманометра
Величина  определяется из условия, что объем жидкости, вытесненной из бачка, равен объему жидкости, поднявшейся в трубке определяется из условия, что объем жидкости, вытесненной из бачка, равен объему жидкости, поднявшейся в трубке
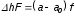
или
 (1.8) (1.8)
где  - площадь поперечного сечения трубки; - площадь поперечного сечения трубки;
 - площадь поверхности жидкости в бачке. - площадь поверхности жидкости в бачке.
Подставляя выражения (7) и (8) в (6) получим следующее выражение
 . .
После несложных преобразований, с учетом коэффициента насадка  , получим формулу, которая непосредственно связывает скоростной напор с показаниями шкалы микроманометра , получим формулу, которая непосредственно связывает скоростной напор с показаниями шкалы микроманометра
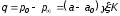 , (1.9) , (1.9)
где  - коэффициент манометра, его величина для каждого угла наклона измерительной трубки указана в техническом паспорте микроманометра. - коэффициент манометра, его величина для каждого угла наклона измерительной трубки указана в техническом паспорте микроманометра.
Таким образом, система приборов: ПВД плюс микроманометр, позволяет определить скоростной напор в потоке.
В реальном потоке в рабочей части аэродинамической трубы всегда существует в той или иной мере неравномерность поля скоростных напоров. Скоростной напор в месте установки ПВД не совпадает со скоростным напором в месте положения исследуемой модели. Для определения скоростного напора в месте модели в формулу (9) вводится коэффициент поля трубы 
 . (1.10) . (1.10)
Коэффициент поля трубы является характеристикой аэродинамической трубы. Его значения определяются при метрологической аттестации трубы для выбранных точек потока в рабочей части и заносятся в технический паспорт трубы.
С учетом формулы (10) выражение для определения скорости потока принимает вид
 (1.11) (1.11)
Удельный вес (и плотность) жидкости зависят от ее температуры. Для исключения погрешности необходимо величину  пересчитать для температуры эксперимента по формуле пересчитать для температуры эксперимента по формуле
 , ,
где  - удельный вес жидкости в микроманометре при температуре - удельный вес жидкости в микроманометре при температуре  = 15C ; = 15C ;
 - то же, при температуре эксперимента - то же, при температуре эксперимента  ; ;
 - коэффициент объемного расширения жидкости. - коэффициент объемного расширения жидкости.
Для спирта  = 7793 Н/м3 при 15 С, а = 7793 Н/м3 при 15 С, а  = 0,0011 1/град. Поэтому для получения ошибки в величине = 0,0011 1/град. Поэтому для получения ошибки в величине  1% разность температур 1% разность температур  должна быть не более 10. При меньшей разности температур должна быть не более 10. При меньшей разности температур  температурной поправкой на изменение плотности жидкости в манометре можно пренебречь. температурной поправкой на изменение плотности жидкости в манометре можно пренебречь.
1.2.7. Схема установки
Схема установки приведена на рис. 1.8. В рабочую часть аэродинамической трубы 2 помещен ПВД 1. ПВД закреплен на державке 4, позволяющей изменять угол атаки. Каналы полного и статического давления ПВД соединены с микроманометром 3.
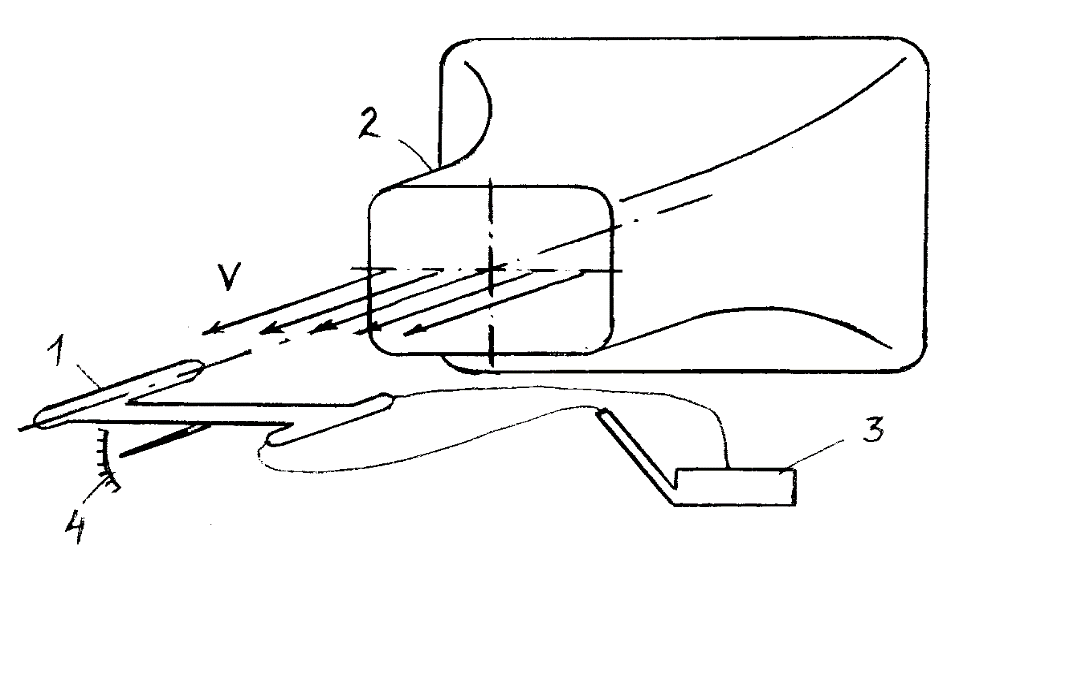
Рис. 1.8. Схема установки
Рабочие формулы
Обычно при обработке результатов эксперимента требуется проведение большого числа однотипных расчетов. Например, в настоящей работе требуется определить погрешность скорости в зависимости от ряда углов атаки ПВД. Полученные теоретические формулы не очень удобны для этого. Чтобы сделать их более удобными для расчетов, в формулах выделяют величины, которые постоянны в данном эксперименте. Эти величины объединяют в так называемые константы, которые предварительно вычисляют. Формулы, преобразованные таким образом, называют рабочими.
Рассмотрим полученные формулы (1.7) и (1.8)
; .
Величины , , и в процессе эксперимента не меняются, а ме-няются только показания микроманометра. Составив из этих величин констан-ты
;
получим рабочие формулы
; .
Кроме этого в лабораторной работе нужно определить точность измере-ния скоростного напора и скорости при различных углах атаки ПВД. Для этого нужно вычислить относительные погрешности для скоростного напора и скорости по рабочим формулам
%
где и - величины, полученные при заданных углах атаки;
и -величины, полученные при угле атаки равном нулю.
Обычно при систематических экспериментах (многократно повторяю-щихся) результаты оформляют в виде таблиц.
Анализируя вышеприведенные формулы, можно составить табл. 1.1 для записи и обработки результатов эксперимента.
Число строк в таблице зависит от количества углов и уточняется у преподавателя.
Таблица 1.1
Результаты измерения скорости воздушного потока
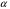
| 
| 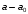
| q | V | 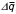
| 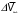
| -45 -30 -15 0 15 30 45 |
|
|
|
|
|
|
ВЫПОЛНЕНИЕ ЭКСПЕРИМЕНТА И ПОЛУЧЕНИЕ
РЕЗУЛЬТАТОВ
Порядок обработки результатов эксперимента
1. На основе изучения темы лабораторной работы и порядка проведения эксперимента выписать рабочие формулы и составить таблицу для занесения экспериментальных и расчетных результатов.
2. Вычислить плотность воздуха.
3. Вычислить константы в рабочих формулах.
4. Вычислить скоростной напор для каждого угла атаки ПВД.
5. Вычислить скорость потока для каждого угла атаки ПВД.
6. Вычислить относительную погрешность скоростного напора для каж-дого угла атаки.
7. Вычислить относительную погрешность скорости для каждого угла атаки.
8. Построить графики зависимостей
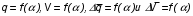
9. Определить диапазоны углов атаки, обеспечивающие относительную погрешность для 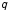 и и 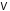 не более 5%. не более 5%.
10. Провести анализ результатов и сделать выводы о точности пневмо-метрического метода измерения скорости.
Оформление отчета
Отчет по лабораторной работе должен содержать:
Титульный лист (рис. 1.1).
Цель лабораторной работы.
Тезисы теоретического материала: основные определения, понятия и формулы; рисунки, указанные преподавателем.
Рисунок схемы лабораторной установки.
Рабочие формулы, по которым проводятся расчеты.
Расчетные или измеренные, не изменяющиеся в процессе эксперимента, газодинамические параметры воздушного потока.
Таблицу с экспериментальными и расчетными данными.
Графики.
Выводы. |
|
|
 Скачать 278.62 Kb.
Скачать 278.62 Kb.
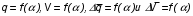
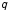 и
и 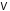 не более 5%.
не более 5%.



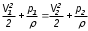
 (1.1)
(1.1) - скоростной напор или динамическое давление
- скоростной напор или динамическое давление . (1.3)
. (1.3)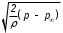 . (1.4)
. (1.4)
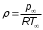 ,
,
 .
. , (1.6)
, (1.6)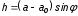 , (1.7)
, (1.7)
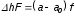
 (1.8)
(1.8) .
.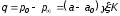 , (1.9)
, (1.9) (1.11)
(1.11) ,
,