фааыаф. Лабораторные работы. Лабораторная работа 1 Знакомство с системой схемотехнического моделирования MicroCap 9

Название	Лабораторная работа 1 Знакомство с системой схемотехнического моделирования MicroCap 9
Анкор	фааыаф
Дата	02.12.2020
Размер	1.79 Mb.
Формат файла
Имя файла	Лабораторные работы.doc
Тип	Лабораторная работа #155985
страница	10 из 10

1 2 3 4 5 6 7 8 9 10

Лабораторная работа № 6

Временная дискретизация аналоговых сигналов

I. Цель работы

С помощью программы Micro-Cap осуществить дискретизацию различных аналоговых сигналов

II. Предварительный расчет

1. Провести дискретизацию аналогового сигнала с линейно изменяющимся напряжением (рис. 1), определяемого соотношением u₁(t)=4t B на отрезке t[0,1]мс, при k=0,1,...,10 –номера отсчетов. Интервалы между моментами времени брать одинаковыми.

Полученные данные занести в таблицу 1. Построить график данного дискретного баланса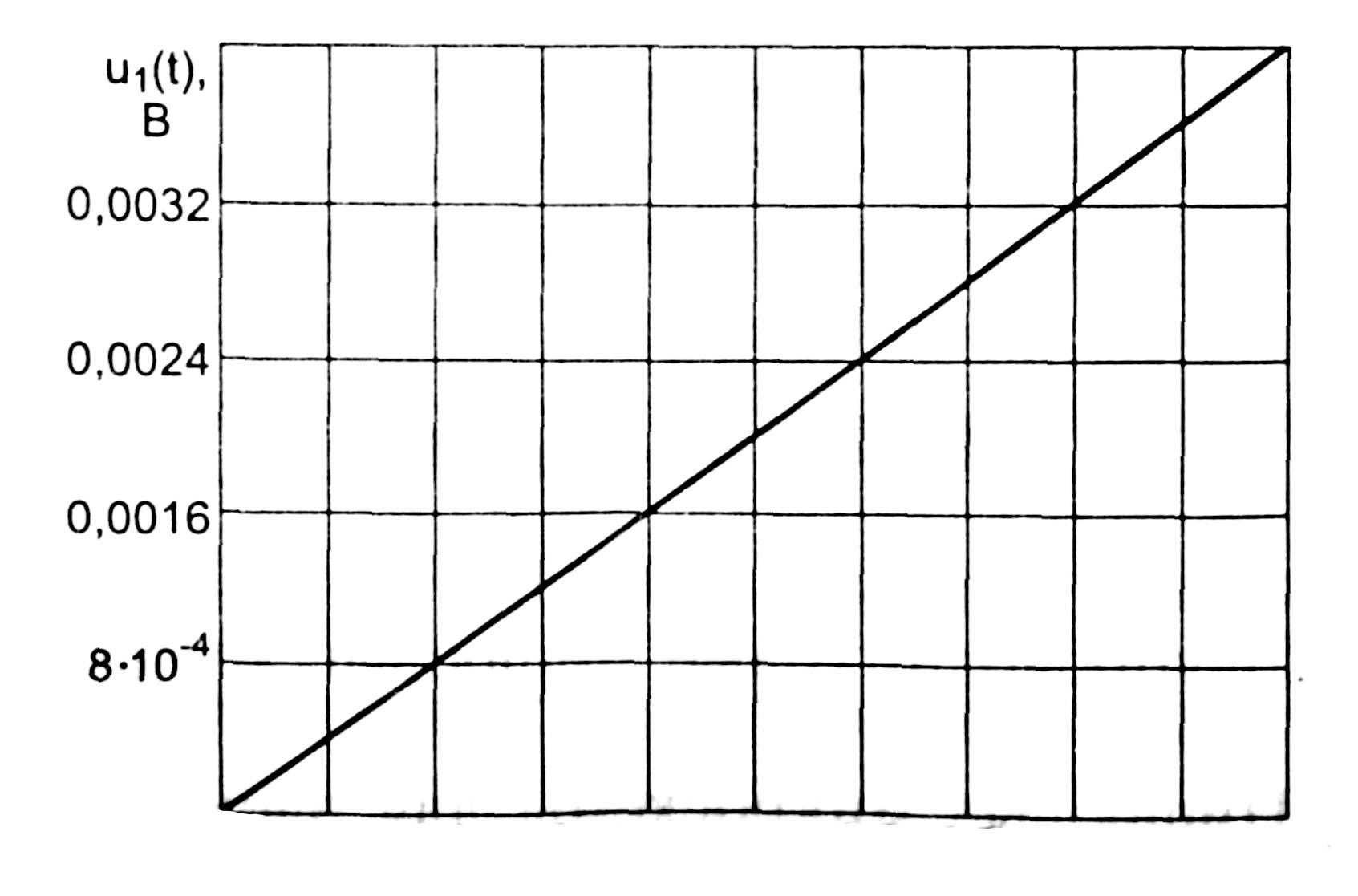

рис. 1

0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1 t,мс

2. Провести дискретизацию аналогового единичного сигнала (рис. 2), определяемого соотношением u₂(t)=1 на отрезке t  [0,1] мс, при k=0,1,...,10 – номера отсчетов. Интервалы между моментами времени брать одинаковыми.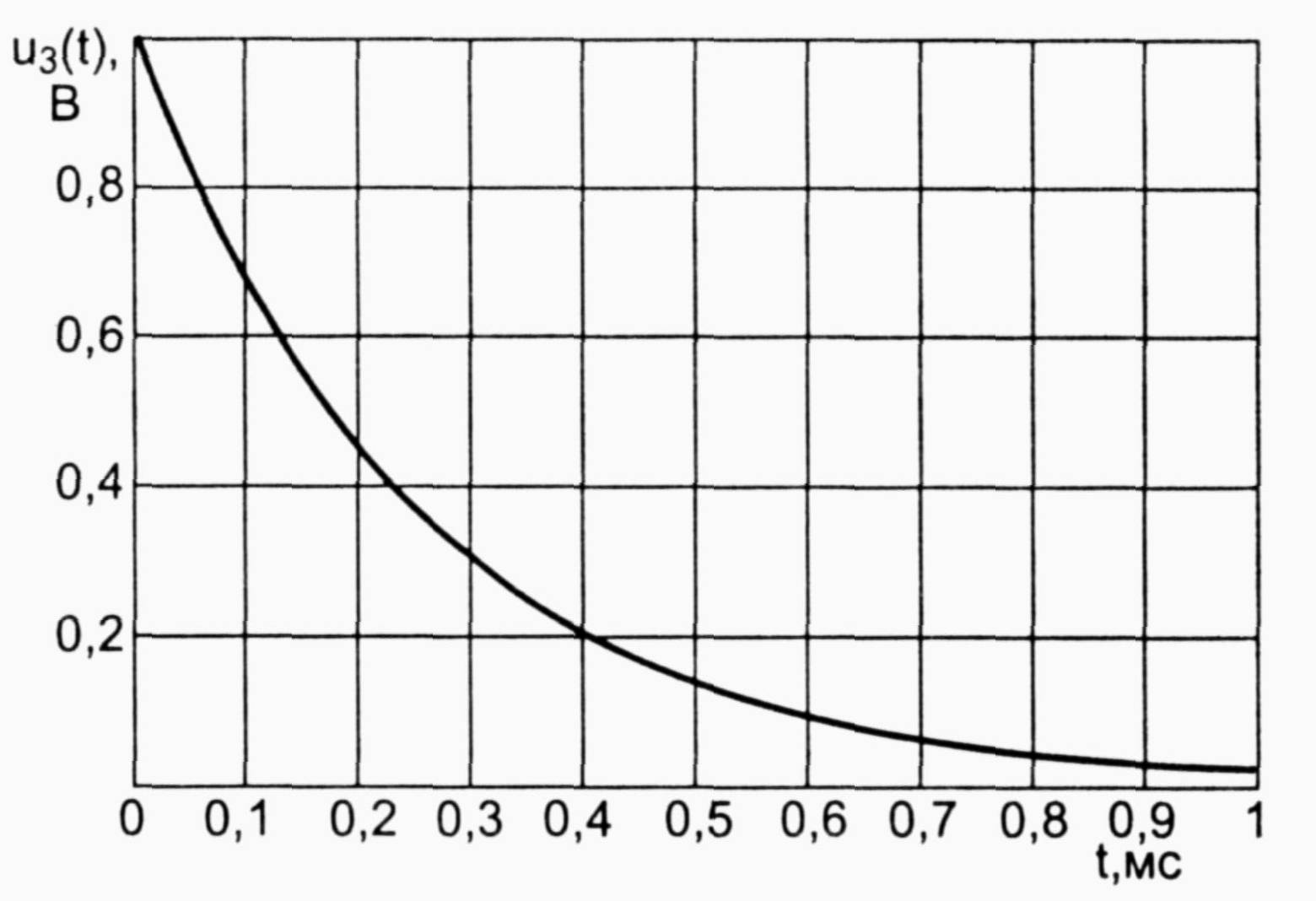

рис. 2

рис. 3

Полученные данные занести в таблицу 1. Построить график дискретного сигнала.

3. Провести дискретизацию аналогового экспоненциального сигнала (рис. 3), определяемого соотношением u₃(t)=exp(-4*10³t) В на отрезке t  [0,1] мс, при k=0,1,...,10 – номера отсчетов. Интервалы между моментами времени брать одинаковыми.

Полученные данные занести в таблицу 1. Построить график дискретного сигнала.

4. Провести дискретизацию аналогового двухполупериодного сигнала (рис. 4), определяемого соотношением u₄(t)=|cos(2ft)| В на отрезке t  [0,1] мс, при k=0,1,...,10 – номера отсчетов, f=1кГц – частота аналогового сигнала. Интервалы между моментами времени брать одинаковыми.

Полученные данные занести в таблицу 1. Построить график дискретного сигнала.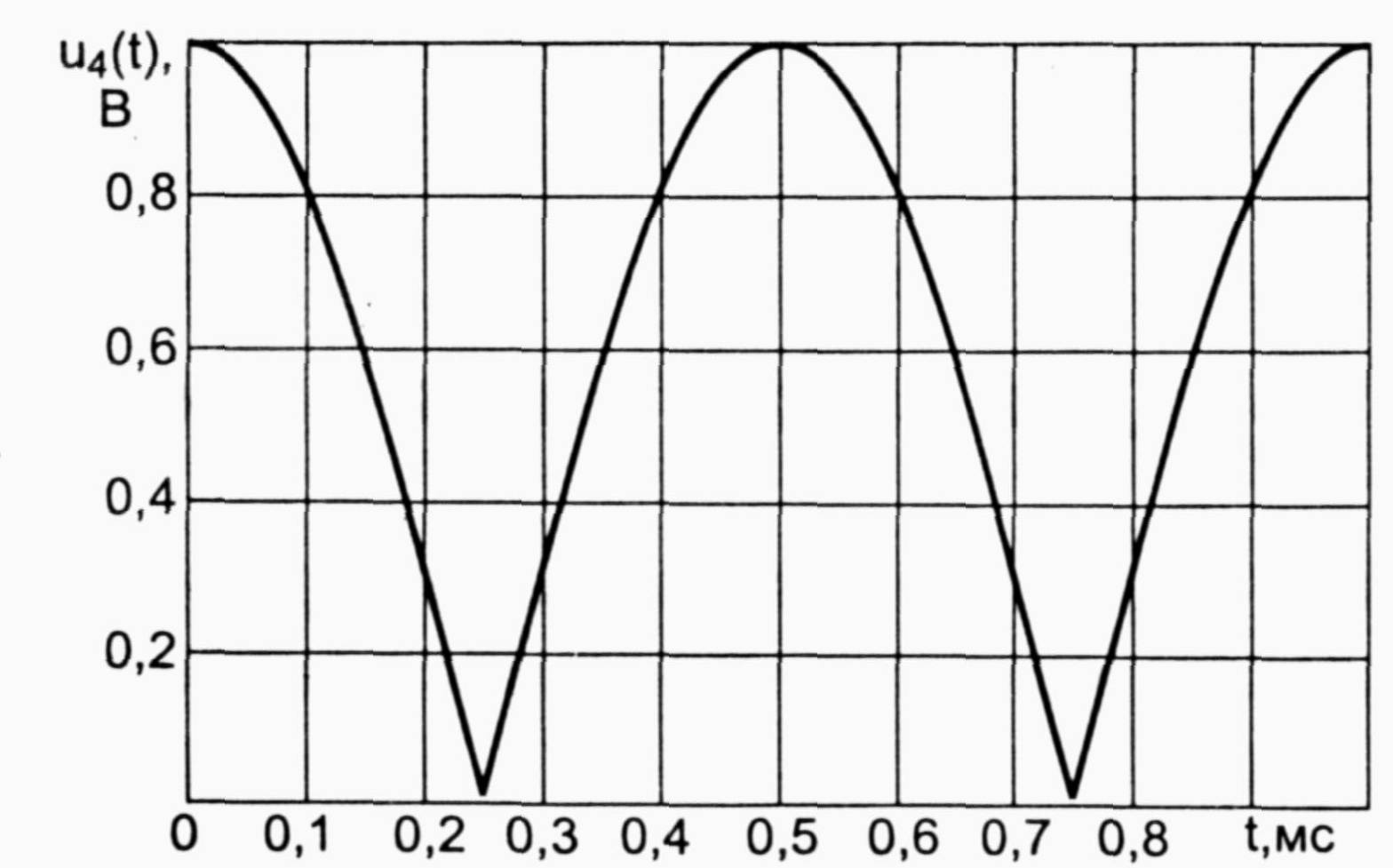

рис. 4

рис. 5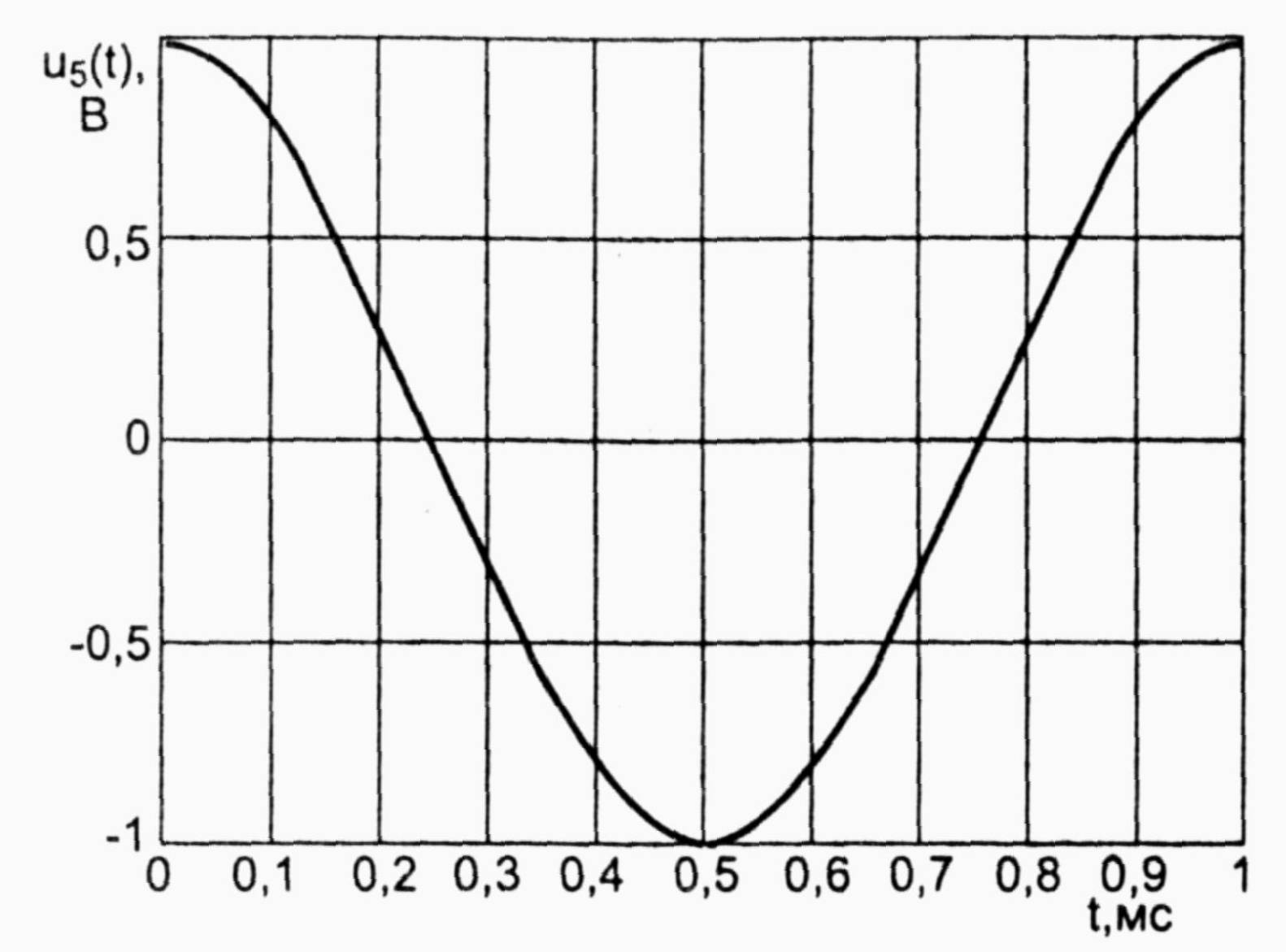

Провести дискретизацию аналогового косинусоидального сигнала (рис. 5), определяемого соотношением u₅(t)=cos(2f t) В на отрезке t  [0,1] мс, при k=0,1,...,10 – номера отсчетов, f=1кГц – частота аналогового сигнала. Интервалы между моментами времени брать одинаковыми.

Полученные данные занести в таблицу 1. Построить график дискретного сигнала.

Таблица 1.

По предварительному расчету
k	t_k	u₁(k)	u₂(k)	u₃(k)	u₄(k)	u₅(k)
1
2
3
4
5
6
7
8
9
10

IV. Порядок выполнения работы

Процесс замены аналогового сигнала его дискретными отсчетами обычно через равные промежутки времени, называется дискретизацией сигнала по времени.

Отсчеты дискретного сигнала определены для дискретных значений независимой переменной времени и представляются последовательностью чисел. Такую последовательность чисел можно записать в следующем виде

u(k)={u(k)}={..., u(-2), u(-1), u(0), u(1), u(2), ...}, -<k<.

Дискретный сигнал обычно изображают в виде следующего графика рис. 6.

Заметим, что дискретный сигнал u(k) определен только для целых значений k . Для не целых значений k дискретный сигнал не определен.

Например, дискретный единичный импульс (рис.7) определяется формулой:

Дискретная единичная ступенчатая функция (рис. 8) определяется следующим образом: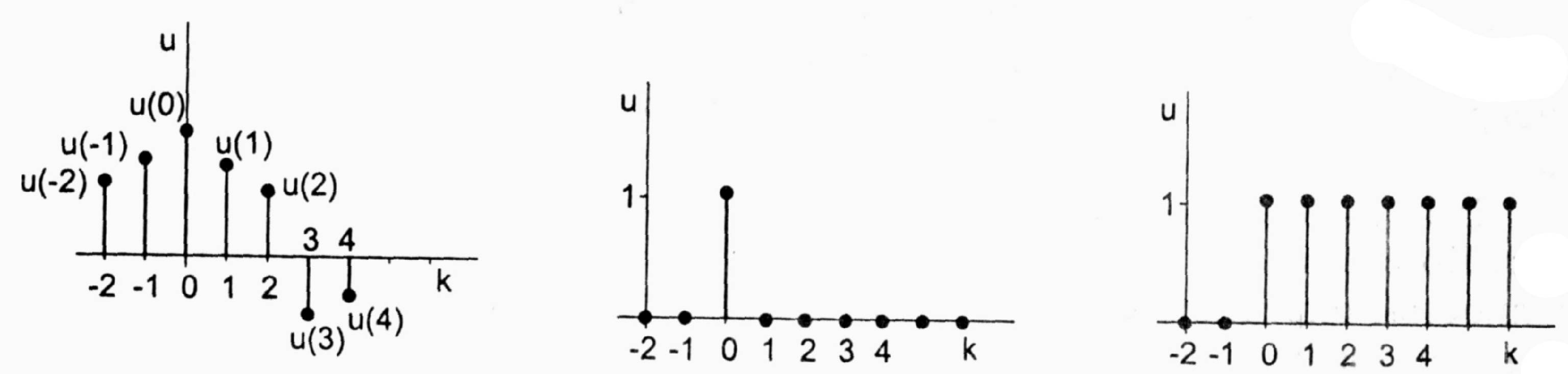

рис. 6

рис. 7

рис. 8

Интервал времени T, через который берутся отсчеты аналогового сигнала, называется интервалом дискретизации. Величина f_Д= 1/T называется частотой дискретизации. Значения дискретного сигнала в тактовые моменты называются отсчетами или выборками. Если частота дискретизации достаточно большая и превышает частоту аналогового сигнала, то дискретные отсчеты позволят правильно восстановить аналоговый сигнал (рис. 9).

если частота дискретизации небольшая по сравнению с частотой сигнала, то в этом случае дискретные отсчеты могут не позволить правильно восстановить сигнал.(рис. 10).

рис. 9

рис. 10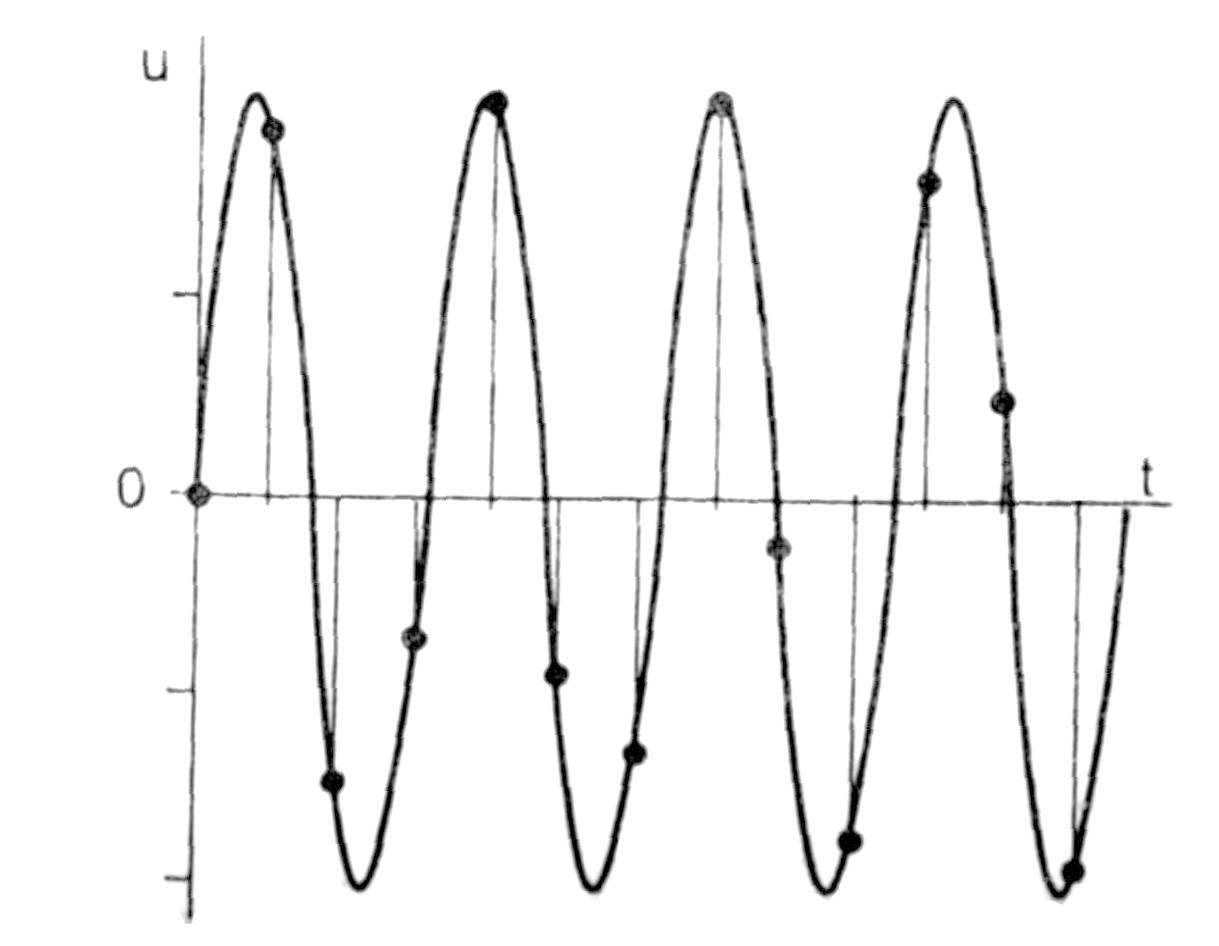

Если частота аналогового сигнала значительно больше частоты дискретизации, то наблюдается эффект ложной частоты. (рис. 11)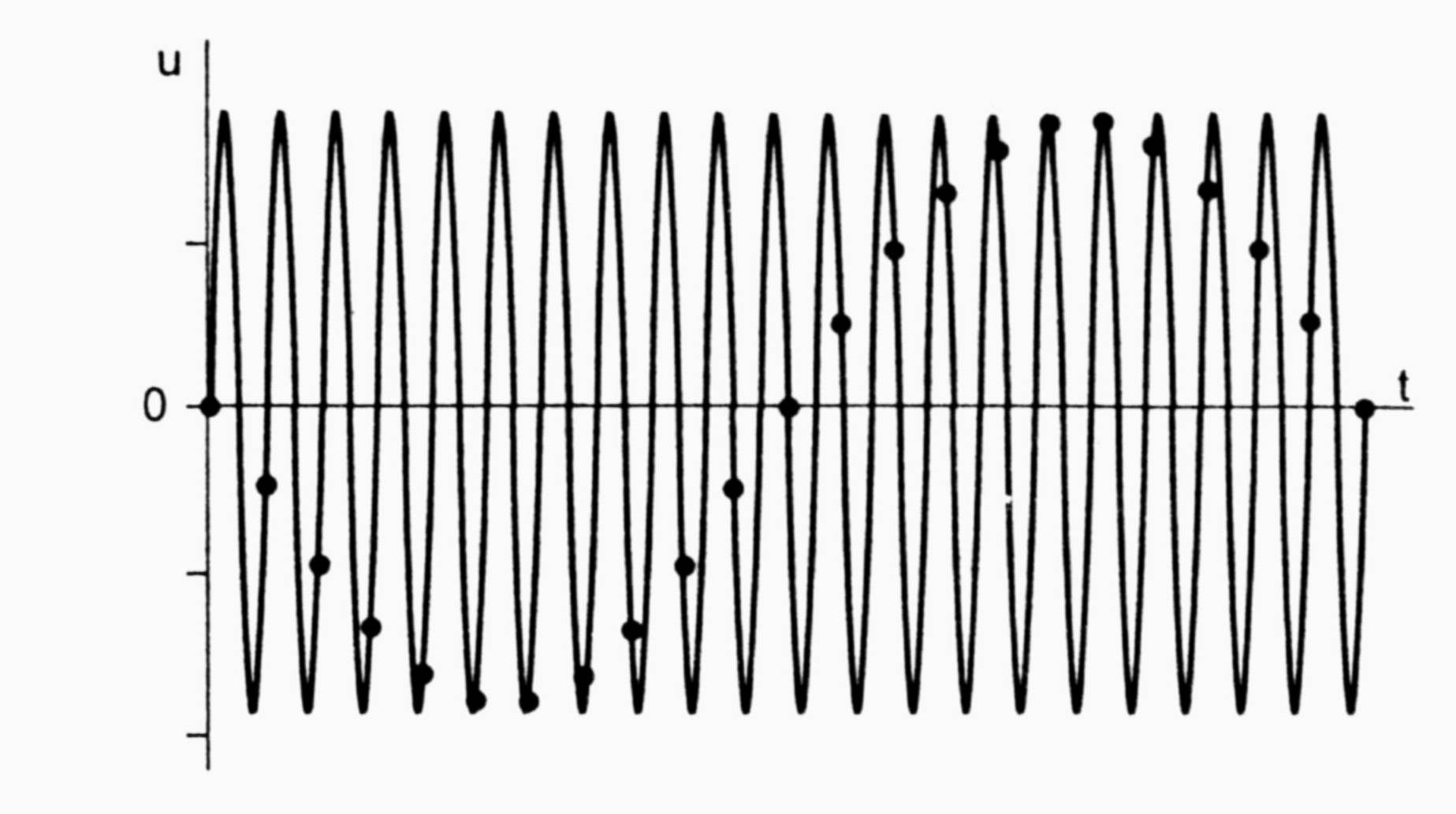

рис. 11

Как видно из этих графиков, неправильный выбор частоты дискретизации аналоговых сигналов может привести к потери информации, поскольку дискретный сигнал не учитывает поведение аналогового сигнала в промежутках между отсчетами.

Для правильного выбора частоты дискретизации следует использовать теорему Котельникова. Аналоговый сигнал, не содержащий частот выше F_max(Гц), полностью определяется последовательностью своих значений в моменты времени, отстоящие друг от друга на 1/(2F_max).

Так в современных цифровых аудиосистемах частоту дискретизации выбирают с запасом по отношению к теоретическому пределу слышимости в 20 кГц. В таких системах частота дискретизации равна 44,1 или 48 кГц.

В студийной аппаратуре обычно используют частоты дискретизации 56, 96 или 192 кГц. Это делается для того, чтобы сохранить не воспринимаемые человеческим ухом высокочастотные гармоники звукового сигнала, которые вносят заметный вклад в формирование общей звуковой картины. частоту дискретизации для телефонных сигналов выбирают равной 8 кГц.

Получить дискретный сигнал из аналогового сигнала можно применив принцип импульсной амплитудной модуляции. Импульсный модулятор можно представить как умножитель с двумя входами и одним выходом.

На первый вход импульсного модулятора подается аналоговый сигнал, подлежащий дискретизации. На второй вход подается последовательность коротких синхронизирующих импульсов, следующих во времени через равные промежутки времени T (интервал дискретизации).

На выходе образуется дискретный сигнал, величина выборок которого будет пропорциональна величине аналогового сигнала в точках отсчета (рис. 12).

Математическая модель дискретного сигнала может быть записана в следующем виде: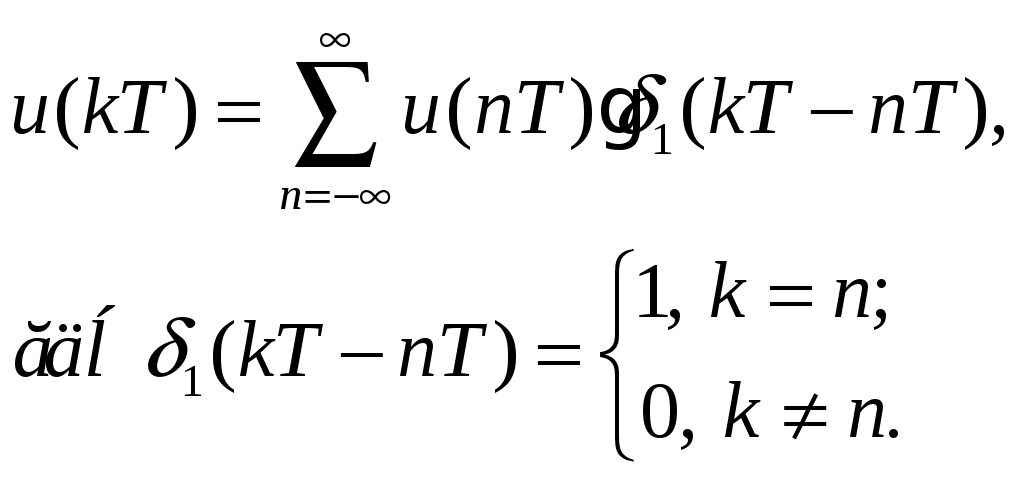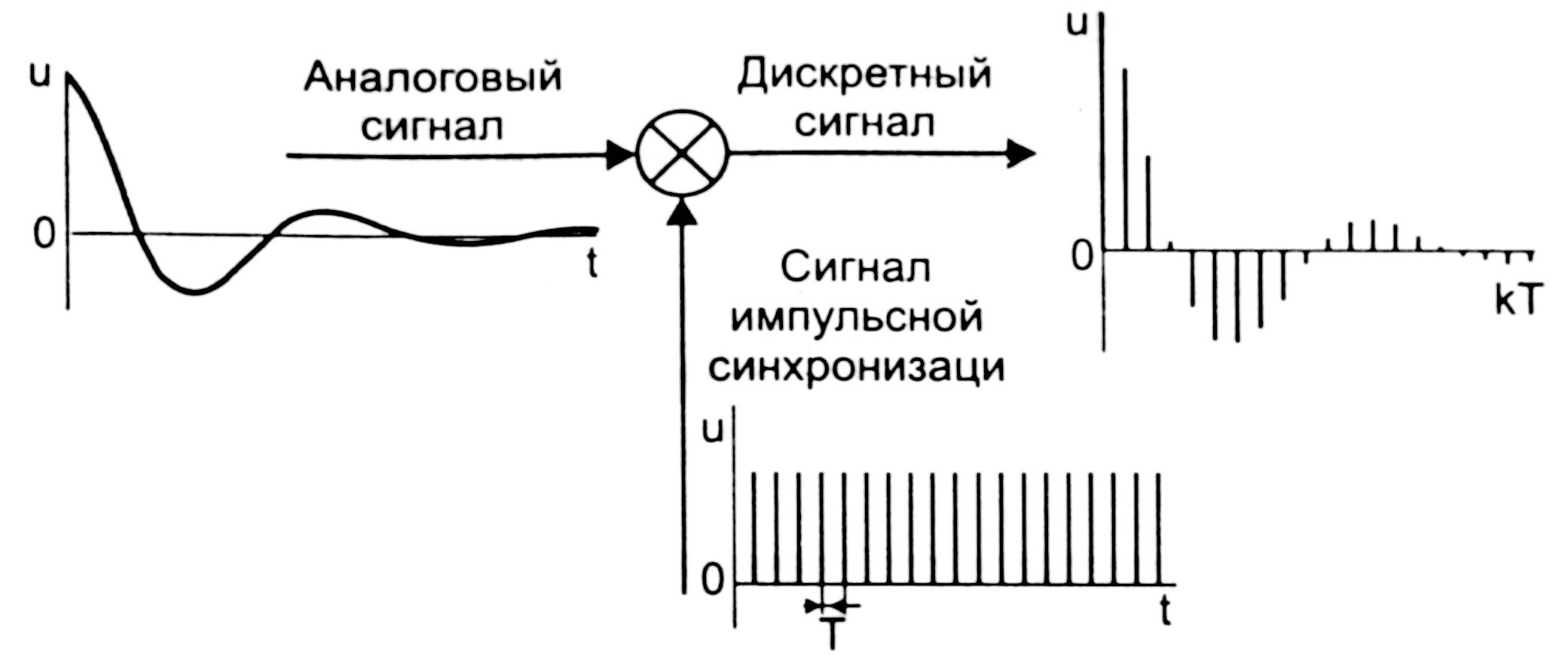

рис. 12

Заметим, что все члены данной суммы при n≠k равны нулю.

Получим из аналоговых сигналов их дискретные аналоги с помощью программы Micro-Cap.

V. Моделирование

1. Сборка схемы импульсного амплитудного модулятора.

Соберите схему импульсного амплитудного модулятора, состоящую из двухвходового умножителя, источника аналогового сигнала, источника синхроимпульсов и земли.

Сначала введите источник аналогового сигнала с линейно нарастающим напряжением u(t)=4t (E1) из меню Component\Analog Primitives\Function Sourses - выберите NFV.

В коне NFV введите 4*t в окне Value, а в окне Show установите галочку. Снизу от источника введите землю.

Введите умножитель сигналов Component\Analog Primitives\Macros и выберите Mul.

Введите источник синхроимпульсов с тактовым периодом T=0,01 мс (f_Д=100 кГц) и амплитудой узких импульсов 1 В. Данный источник будет состоять из генератора импульсов DClock (X2) и усилителя Amp(X3).

Откройте меню Component\Digital Primitives\Stimulus is Generators и выберите команду DClock . В появившемся окне Digital Clock Marcro для генерации узких синхроимпульсов задайте временные параметры:

Param:Zerowidth=0.01 m

Param:Onewidth=0.001 m (длина импульса)

Для того чтобы на второй вход умножителя поступали синхроимпульсы с амплитудой 1В, последовательно с генератором включите усилитель с коэффициентом усиления 0,2 (GAIN=0.2), введите усилитель Amp(X3) из меню Component\Analog Primitives\Macros\Amp. В окне Amplifier Macro введите значение коэффициента усиления 0.2 в поле Value.

Соедините все элементы схемы проводниками, как показано на рисунке: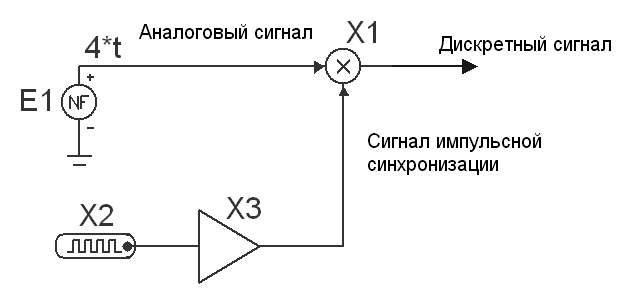

2. Дискретизация линейно изменяющегося напряжения

С помощью меню Analysis команды Transient... постройте графики заданного аналогового и дискретного сигнала со следующими параметрами:

Time Range – 1m – временной интервал (0...1мс)

Maximum Time Step – 0.001m – максимальный шаг (0,001 мс)

P номер окна - 1, в котором будет построен график аналогового сигнала.

X Expression – t – аргумент функции

Y Expression – V(E1) – имя функции

P номер окна - 2 , в котором будет построен график аналогового сигнала.

Y Expression – V(3) – имя функции

X Range – Auto – интервал отображения аргумента по оси X

Y Range – Auto - интервал отображения аргумента по оси Y

Данные графики занесите в отчет.

Далее, в полях XRange, YRange – следует вводить Auto (!)

3. Дискретизация аналогового единичного сигнала

Для проведения дискретизации аналогового единичного сигнала вернитесь к исходной схеме. Два раза щелкните по элементу E1. В поле Value вместо 4*t величину единичного сигнала – «1».

Постройте графики получившихся сигналов. Графики занесите в отчет.

4. Дискретизация аналогового экспоненциального сигнала

Вернитесь к исходной схеме, измените характеристики элемента E1 аналогично предыдущему пункту. В поле Value введите формулу сигнала: exp(-4E3*t)

Постройте графики получившихся сигналов. Графики занесите в отчет.

5. Дискретизация аналогового двухполупериодного сигнала.

Вернитесь к исходной схеме, измените характеристики элемента E1 аналогично предыдущему пункту. В поле Value введите формулу сигнала: abs(cos(2*pi*t*1E3)).

Постройте графики получившихся сигналов. Графики занесите в отчет.

6. Дискретизация аналогового косинусоидального сигнала.

Вернитесь к исходной схеме, измените характеристики элемента E1 аналогично предыдущему пункту. В поле Value введите формулу сигнала: cos(2*pi*t*1E3)

Постройте графики получившихся сигналов. Графики занесите в отчет.

7. Эффект ложной частоты.

Для наблюдения эффекта ложной частоты (рис. 11) необходимо увеличить частоту косинусоидального сигнала до 95 кГц (95E3). Для этого вернитесь к исходной схеме, измените характеристики элемента E1 – в поле Value введите cos(2*pi*t*95E3).

Постройте графики дискретного и аналогового сигналов (при f=0.95f_Д).

На экране появятся два графика: аналоговый и дискретный сигнал. На нижнем графике отчетливо проявился эффект ложной частоты. Данные графики занесите в отчет.

Аналогично уменьшите частоту косинусоидального сигнала до 31 кГц (31E3). Получите графики сигналов в этом случае. Сделайте вывод о возможности восстановления данного сигнала. Проверьте выполнение теоремы Котельникова. Занесите графики в отчет.

1 2 3 4 5 6 7 8 9 10