Лаба №10. Лабораторная работа 10 I. Название работы Изучение законов вращательного движения твердого тела. Цель работы

• Название: Лабораторная работа 10 I. Название работы Изучение законов вращательного движения твердого тела. Цель работы
• Дата: 24.05.2023
• Размер: 1.95 Mb.
• Имя файла: Лаба №10.doc
• Тип: Лабораторная работа; #1157053

Дата Фамилия Группа
Лабораторная работа № 10
I.Название работы:

Изучение законов вращательного движения твердого тела.

Цель работы:

1.Проверка зависимости углового ускорения ε от момента силы М при постоянном моменте инерции J.

2.Проверка зависимости момента инерции J грузов от расстояния до оси вращения.
II.Краткое теоретическое обоснование:

Векторы перемещения Δ r, скорость v и ускорение а различны для различных точек тела, для характеристики вращательного движения удобнее использовать угол поворота φ, угловую скорость ω - угловое ускорение ε, одинаковые для всех точек твёрдого тела.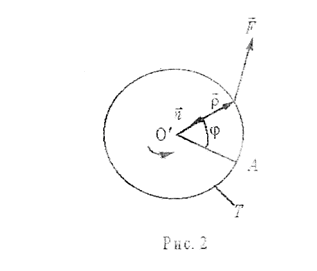


Рассмотрим движение точки А. Она движется по окружности Т, центр которой О’ располагается оси z . Для определения угла поворота φ вектора p, определяющего положение точки А, введем неподвижную линию О’А. Пусть р за время dt поворачивается на угол dφ в указанном направлении ( рис.2). Представим малый угол поворота в виде вектора dφ направленного вдоль оси и его направление определим следующим образом: если смотреть с конца вектора z, вращение на угол аφ видно происходящим против направления движения по часовой стрелке.

Моментом инерции материальной точки относительно оси z называется произведение её массы m_i на квадрат расстояния r_i от материальной точки до оси вращения

J_i= m_i r_i²

Основной закон динамики вращательного движения твердого тела вокруг неподвижной оси z записывается в виде

M_z=ε J_z ,

где J_z – момент инерции тела относительно оси z .
III.Рабочие формулы и единицы измерения.

а=2h/t² [м/с² ] M=m(g-2h/t² ) [Н·м] ε=a_τ/r=2h/t²r [c^-2]
IV.Схема установки.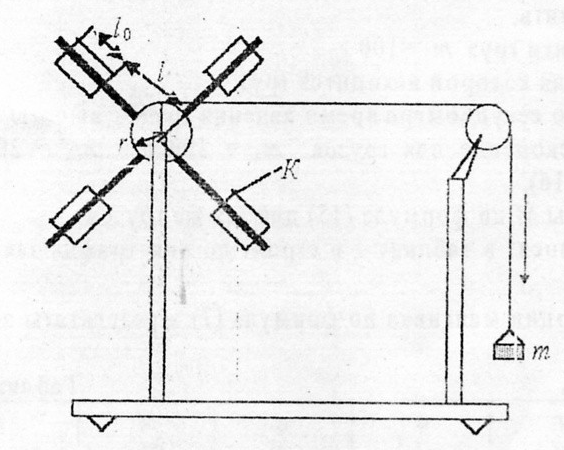


V.Измерительные приборы и принадлежности:

1. 
   Маятник Обербека.
   
2. 
   Электросекундомер.
   
3. 
   Метровая линейка.
   
4. 
   Штангенциркуль.
   

VI.Результаты измерения.

Таблица 1

m кг	t с	r м	a м/с2	ε c-2	M Н·м	Jz кг·м2
0,1	9	0,424	0,004	0,25	0,017	0,01798
0,2	5	0,424	0,0144	0,82	0,034	0,03596
0,3	4	0,424	0,0225	1,30	0,051	0,05393

№ п/п	m кг	h м	M Н·м	ε c-2	t с	a м/с2	R2 м	Jz кг·м2
1	0,1	0,18	0,01714	0,25	9	0,004	0,2175	0,06856
2	0,1	0,18	0,01713	0,42	7	0,007	0,1875	0,04
3	0,1	0,18	0,01710	1,29	4	0,023	0,1575	0,013
4	0,1	0,18	0,01709	1,68	3,5	0,029	0,1275	0,0101
5	0,1	0,18	0,01708	2,05	3,17	0,036	0,0975	0,0083

Таблица 2
VII.Черновые записи и вычисления.

h=0,18
a=(2·0,18)/81=0,004 a=(2·0,18)/25=0,0144 a=(2·0,18)/16=0,0225
M=0,1(9,8-(2·0,18)/81)·0,0175=0,017 M=0,2(9,8-(2·0,18)/25)·0,0175=0,034

M=0,3(9,8-(2·0,18)/16)·0,0175=0,051
ε=(2·0,18)/(81·0,0175)=0,25 ε=(2·0,18)/(25·0,0175)=0,82 ε=(2·0,18)/(16·0,0175)=1,3
J_z=0,1·(0,424)²=0,1·0,179776=0,01798 J_z=0,2·(0,424)²=0,2·0,179776=0,03596

J_z=0,3·(0,424)²=0,3·0,179776=0,05393
l₁=0,205 l₂=0,175 l₃=0,145 l₄=0,115 l₅=0,085
R₂=0,205+0,0125=0,2175 R₂=0,175+0,0125=0,1875 R₂=0,145+0,0125=0,1575

R₂=0,115+0,0125=0,1275 R₂=0,085+0,0125=0,0975
ε=(2·0,18)/(81·0,0175)=0,25 ε=(2·0,18)/(49·0,0175)=0,42 ε=(2·0,18)/(16·0,0175)=1,29 ε=(2·0,18)/(12,25·0,0175)=1,68 ε=(2·0,18)/(10,0489·0,0175)=2,05
M=0,1(9,8-(2·0,18)/81)·0,0175=0,01714 M=0,1(9,8-(2·0,18)/49)·0,0175=0,01713

M=0,1(9,8-(2·0,18)/16)·0,0175=0,0171097

M=0,1(9,8-(2·0,18)/12,25)·0,0175=0,017099

M=0,1(9,8-(2·0,18)/10,0489)·0,0175=0,017087

a=(2·0,18)/81=0,004 a=(2·0,18)/49=0,007 a=(2·0,18)/16=0,023 a=(2·0,18)/12,25=0,029 a=(2·0,18)/10,0489=0,036
VIII.Основные выводы.

1. 
   Проверили зависимость углового ускорения ε от момента силы М при постоянном моменте инерции.
   
2. 
   Проверили зависимость момента инерции J грузов от расстояния до оси вращения.
   

IX.Графики.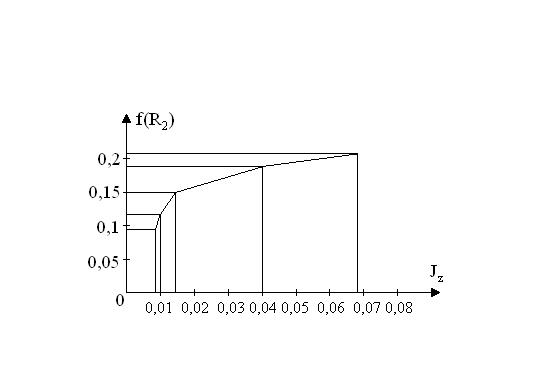