модуль юнга. Лабораторная работа 10 определение модуля упругости (модуля юнга) по деформации изгиба
 Скачать 0.57 Mb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «  Санкт-Петербургский горный университет» КАФЕДРА ОБЩЕЙ И ТЕХНИЧЕСКОЙ ФИЗИКИ ОТЧЕТ ЛАБОРАТОРНАЯ РАБОТА № 10 «ОПРЕДЕЛЕНИЕ МОДУЛЯ УПРУГОСТИ (МОДУЛЯ ЮНГА) ПО ДЕФОРМАЦИИ ИЗГИБА» Выполнил: студент гр. ГГ-21-2 _________ /Карташова У.А./ (подпись) (Ф.И.О.) Проверил: _________ / / (подпись) (Ф.И.О.) Санкт-Петербург 2021 Цель работы: Определение модуля Юнга материала путем измерения прогиба стержня при механической нагрузке. Краткое теоретическое содержание: Явление, изучаемое в работе: деформация твердых тел. Определение основных физических понятий, объектов, процессов и величин. Деформация – изменение размеров и формы. Упругая деформация – деформация, исчезающая после прекращения действия силы. Законы и соотношения, на основании которых получены расчетные формулы: F = kl- величина абсолютной деформации l пропорциональна приложенной силе F: k – постоянная величина для данного образца. 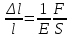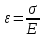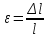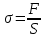Закон Гука при деформации:  или  где  - деформация или относительное изменение длины стержня,  - нормальное механическое напряжение, измеряемое силой, действующей на единицу площади поперечного сечения стержня;E – коэффициент пропорциональности, который называется модулем упругости (модулем Юнга). 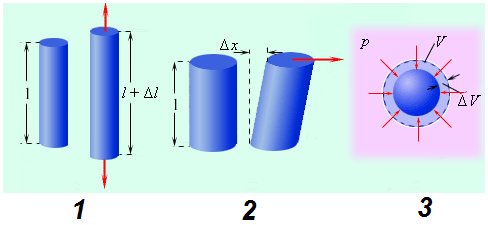 Рис. 1 Явление деформации Определение основных физических понятий, объектов, процессов и величин: Стрелой прогиба Y называется величина прогиба в единицах длины. Схема установки Исследуемым объектом является стержень из неизвестного материала, установленный на две опоры и нагруженный посередине.    Рис. 2 Экспериментальная установка и измеритель стрелы прогиба Установка (рис.2) представляет собой стержень из исследуемого материала 1, расположенный горизонтально и своими концами свободно опирающийся на две призмы 2, обращенными рабочими ребрами вверх. Призмы установлены на вертикальных стойках поперечно по отношению к оси балки. Посередине стержня на него надета серьга 3, к которой подвешена платформа 4 с грузами 6. Стрела прогиба измеряется с помощью механического индикатора 5. Индикатор закреплен на общем основании с опорными стойками балки. Расчетные формулы: а. Закон Гука: деформация, возникающая в упругом теле, пропорциональна приложенной к этому телу силе. 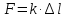 k – постоянная величина для данного образца; 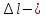 величина абсолютной деформацииб. Сила тяжести F = mg m - масса груза, кг; g – ускорение свободного падения, м/с2 в. Стрела прогиба Y = a0n a0 – цена деления индикатора; n - - отсчет по шкале индикатора прогиба, г. Модуль Юнга 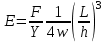 F - приложенная в центре стержня сила, Н; w и h - размеры поперечного сечения стержня, м; Y - стрела прогиба стержня под нагрузкой, м; L - расстояние между опорами балки, м. д. 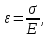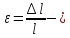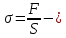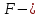Деформация продольного растяжения  где  деформация или относительное изменение длины,м; нормальное напряжение приложенная сила, Н;S – площадь поперечного сечения, м; Е – коэффициент пропорциональности. Формулы погрешностей косвенных измерений 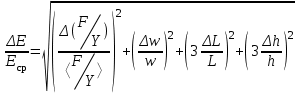 Таблицы Таблица1. Результаты измерения высоты и ширины стержня.
Таблица2. Результаты вычислений и измерений.
Пример вычисления для опыта №1 Исходные данные: w=7 мм - ширина стержня L = 335 мм – расстояние между опорами h = 4 мм – высота стержня Вычисление Сила тяжести F=m·g=0,0495·9,8=0,49 Н Стрела прогиба Y = a0n= 0,0001·10=0,0001 м Отношение силы к стреле прогиба 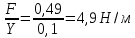 Среднее отношение силы к стреле прогиба 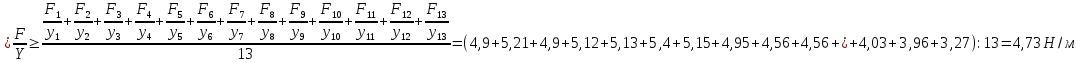 Модуль Юнга 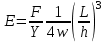= 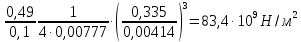абсолютная погрешность косвенных измерений модуля Юнга 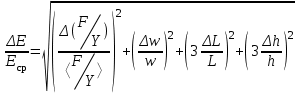= 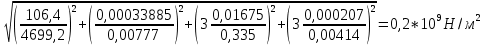Окончательный результат: Модуль Юнга Еср=83,4·109 ±0,2 109 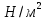 Графический материал  Рис. 3 График зависимости Y от F Вывод В ходе работы был определён модуль упругости (модуль Юнга) материала путем измерения прогиба стержня при механической нагрузке, теоретическое и экспериментальное значения практически совпадают. Полное совпадение значений модуля Юнга, мы не можем наблюдать из-за прямых погрешностей измерений. |