Лабораторная физика. Лабораторная работа 116. Лабораторная работа 116 Определение модуля сдвига из кручения. Теория
 Скачать 90 Kb.
|
|
Лабораторная работа № 116 Определение модуля сдвига из кручения. Теория. Если проволоку или стержень, закрепленный с одного конца, закручивать, прилагая к другому концу пару сил с моментом, равным М, то угол кручения по закону Гука оказывается равным  , где с- коэффициент, зависящий от вещества проволоки. Модуль кручения f, равный  показывает, какой момент нужно приложить, чтобы закрутить проволоку на угол в один радиан. Модуль сдвига N равен  , где  определяет величину касательного усилия на единицу поверхности , а  - угол сдвига.Между модулем кручения и модулем сдвига материала проволоки существует простое соотношение  где r – радиус цилиндрической проволоки, а L – ее длина.Измерение модуля кручения может быть выполнено статистическим или динамическим методом. В первом случае измеряется угол закручивания проволоки под действием определенного закручивающего момента. Во втором случае измеряется период крутильных колебаний маятника, подвешенного на исследуемой проволоке. Динамический метод основан на зависимости периода крутильных колебаний маятника, подвешенного на проволоке, от упругих свойств материала проволоки. Определение модуля сдвига из крутильных колебаний. Если колеблющееся твердое тело совершает вращательные движения, то к нему может быть применен основной закон вращательного движения  , где М –вращающий момент относительно оси вращения, J- момент инерции относительно той же оси и  - угловое ускорение. Обозначая через  вращающий момент, можно написать  . Вращающий момент направлен всегда так, чтобы уменьшить угловое отклонение  .Из этого уравнения видно, что в рассматриваемом движении ускорение  пропорционально угловому смещению и направлено противоположно ему, а это есть существенный признак гармонического колебательного движения. Итак, тело совершает гармонические колебания, а периоды этих колебаний можно найти, вспомнив, что множитель пропорциональности между и , в данном случае  , должен быть равен  , т.е.  , (6), откуда  .Здесь Т- есть период колебания маятника. Для того, чтобы из этого выражения найти f, необходимо исключить неизвестный момент инерции J, для этого в задаче определяются два периода колебаний маятника Т1 и Т2. Работу выполняют следующим образом. Надевают на крайние штифты диска, удаленные от оси вращения четыре груза. Определяют положение равновесия. Системе сообщают вращательный импульс так, чтобы система совершала крутильные колебания с небольшой амплитудой. Измеряют суммарное время 20 колебаний маятника и вычисляют период колебания маятника Т1. Переставив грузы на внутренние штифты, таким же способом измеряют измененный период колебаний Т2. Из этих определений имеем  Откуда  .Момент инерции крутильного маятника можно представить как момент инерции грузов  плюс момент инерции крестовины и проволоки, J. .Для того, чтобы исключить неизвестное J, вычтем J1 из J2.  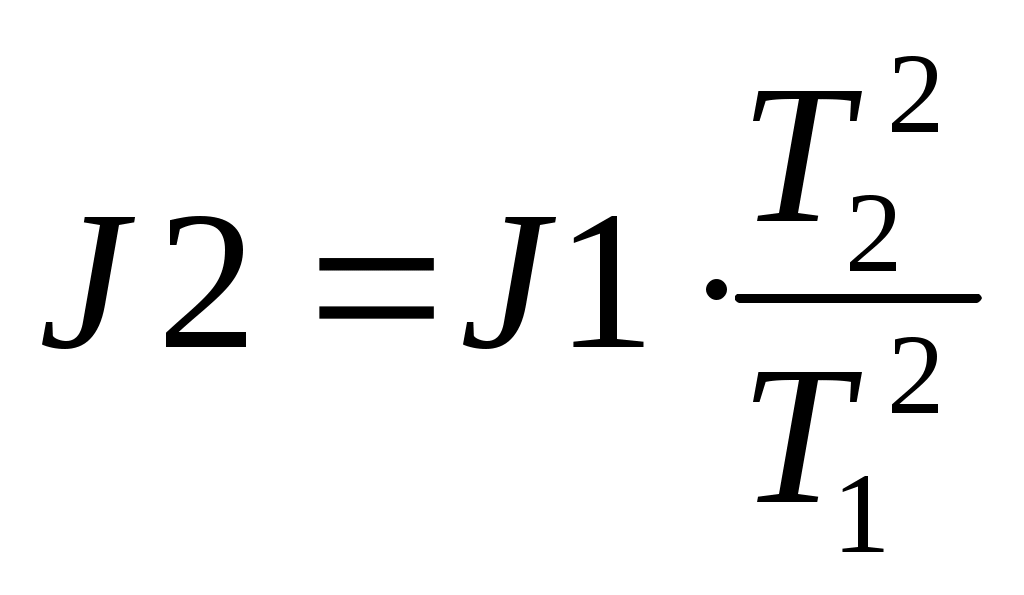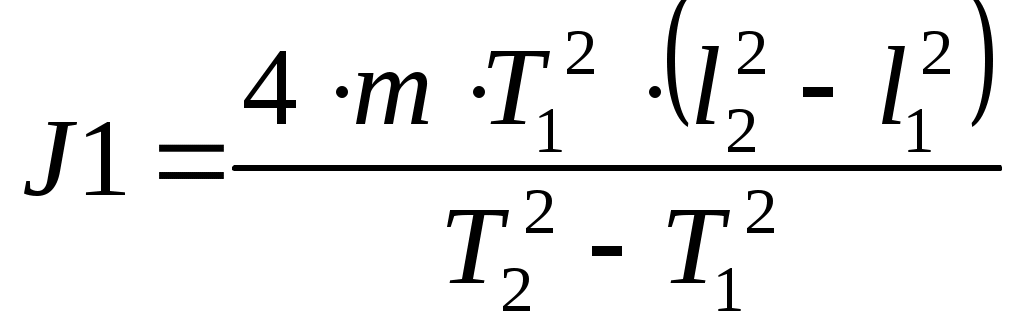(7).Подставив сюда значение  ., из уравнения 7 найдем  .Подставив, наконец, это выражение в уравнение 6, найдем модуль кручения f. 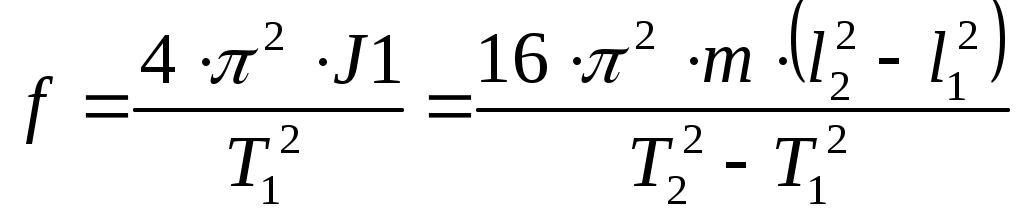 . Определив расстояния осей грузов от оси вращении и их массу, по формуле 3 вычисляют модуль сдвига. Величину модуля сдвига рекомендуется вычислять в 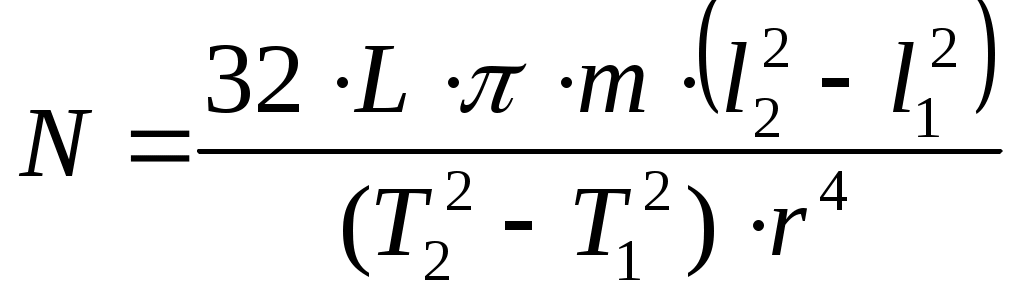 .  .Измерения. Измерить длину проволоки (L), и радиус проволоки(r). Определить массы грузов (m). Закрепить грузы на краях стержней, измерить расстояние от оси вращения до центров грузов (  )Привести систему в колебательное движение. Определить время 50-70 полных колебаний. Вычислить период колебания (Т1). Закрепить грузы на середине стержней. ПОВТОРИТЬ ИЗМЕРЕНИЯ И РАСЧЕТЫ ПУНКТОВ 3 И 4. Результаты измерений и расчетов занести в таблицу. Рассчитать модуль сдвига для данного материала проволоки. По таблицам определите материал проволоки. Сделайте выводы.
Контрольные вопросы. Каков физический смысл модуля кручения? Дайте определение модуля сдвига. Как связаны модуль кручения и модуль сдвига? Как рассчитывается период колебания ФИЗИЧЕСКОГО МАЯТНИКА? Как рассчитать момент инерции крестовины, и грузов на крестовине? Объясните методику определения модуля сдвига. |
