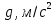Лабораторная работа 152 проверка теоремы штайнера работу выполнили студенты группы 03010 Коротков Алексей Плешаков Даниил Проверил
 Скачать 46.98 Kb. Скачать 46.98 Kb.
|
|
Лабораторная работа №152 ПРОВЕРКА ТЕОРЕМЫ ШТАЙНЕРА Работу выполнили студенты группы: 03-010 Коротков Алексей Плешаков Даниил Проверил: Теория: Основное уравнение динамики вращательного движения в случае неподвижной оси вращения z удобно проектировать на эту ось: 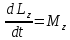 Здесь 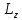 - проекция момента импульса, - проекция момента импульса, 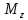 - момент внешних сил относительно оси. - момент внешних сил относительно оси.Проекция момента импульса 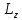 связана с угловой скоростью связана с угловой скоростью 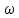 и моментом инерции I относительно этой оси: и моментом инерции I относительно этой оси: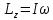 Момент инерции тела определяется формулой:  Где суммирование проводится по всем материальным точками тела с массами 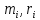 - расстояние от материальным точек до оси вращения. В случае непрерывного распределения масс эту формулу можно записать в интегральном виде: - расстояние от материальным точек до оси вращения. В случае непрерывного распределения масс эту формулу можно записать в интегральном виде: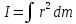 Момент инерции величина аддитивная 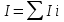 Момент инерции Iтела относительно любой оси AA´ можно найти, зная момент инерции  относительно BB´, проходящей через центр масс тела паралельно оси AA´ при помощи теоремы Гюйгенса-Штайнера: относительно BB´, проходящей через центр масс тела паралельно оси AA´ при помощи теоремы Гюйгенса-Штайнера: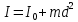 Где m – масса тела, d – расстояние между осями. При вращении тела под действием момента упругой силы пружины уравнение приводит к следующему соотношению: 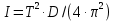 Где 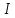 - момент инерции колеблющегося тела, - момент инерции колеблющегося тела, 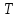 - период колебаний, D-модуль кручения пружины. - период колебаний, D-модуль кручения пружины.Цель работы • Сравнение экспериментально определенной и теоретически показанной зависимости момента инерции диска от расстояния между осью симметрии диска и осью его вращения. Решаемые задачи Измерение моментов инерции диска для различных его положений методом крутильных колебаний. Экспериментальная установка Приборы и принадлежности: Торсионная пружина на штативе. Секундомер. Исследуемый диск. Ход работы. Установили диск на торсионную пружину так, что бы ось колебаний проходила через отверстие 0. Измерили период колебаний 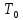 . .Последовательно устанавливали диск так, чтобы ось колебаний проходила через отверстия: 2,4,6,8,10,12,14,16. Измерили радиус диска. Вычислили относительные торические моменты инерции диска по формуле: 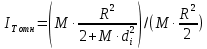 = =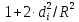 Для всех осей и сравнили с экспериментальными результатами, вычисленными с использованием данных измерения по формуле: 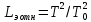 Данные измерений представили в виде таблицы:
Построили график зависимости 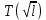 . Выделили на нём линейный участок. По точкам этого участка, пользуясь выражением . Выделили на нём линейный участок. По точкам этого участка, пользуясь выражением 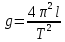 нашли ускорение свободного падения. нашли ускорение свободного падения.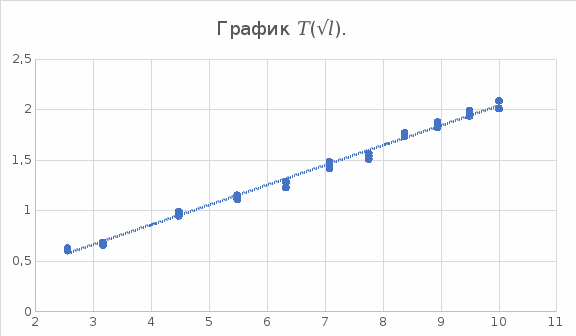 С помощью программы Excel рассчитали значение g для каждого опыта.
Среднее значение g=9,800943 Вывод: таким образом с помощью математического мы смогли определить примерное значение ускорения свободного падения. Мы научились определять скорость свободного падения с помощью математического маятника. |

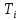 (1)
(1)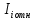
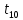 ,c
,c