Главная страница
Навигация по странице:

  • Краткая теория

  • Электромагнитная индукция

  • Закон самоиндукции

  • I

    		•

    Лабораторная работа-электромагнитная индукция. Лабораторная работа 17 Электромагнитная индукция Цель работы


    Скачать 421.23 Kb.
    НазваниеЛабораторная работа 17 Электромагнитная индукция Цель работы
    Дата13.11.2021
    Размер421.23 Kb.
    Формат файлаdocx
    Имя файлаЛабораторная работа-электромагнитная индукция.docx
    ТипЛабораторная работа
    #271167

    Лабораторная работа №17 «Электромагнитная индукция»

    Цель работы:

    1)знакомство с явлением электромагнитной индукции (ЭМИ) и его моделированием;

    2)экспериментальное подтверждение закономерностей ЭМИ.

    Краткая теория:

    Скалярное произведение вектора индукции магнитного поля В на вектор нормали n к данному элементу поверхности и на площадь dS называется элементарным магнитным потоком : . Тогда магнитный поток через поверхность площадью S: 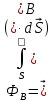.Данное выражение не требует интегрирования если: магнитное поле равно нулю, или вектор магнитной индукции направлен по касательной к поверхности в любой ее точке, угол между вектором индукции и плоскость контура (или нормалью к контуру) постоянен и поле однородно.

    Индукция – явление возникновения одного поля при изменении другого поля. Электромагнитная индукция – явление возникновения электрического поля при изменении потока магнитного поля. Закон ЭМИ: циркуляция электрического поля по замкнутому контуру пропорциональная быстроте изменения потока магнитного поля через поверхность, ограниченную контуром, по которому рассчитана циркуляция. Если проводящее вещество имеет форму замкнутого контура, тогда циркуляция электрического поля в нем по определению является ЭДС, которая в случае ЭМИ называется ЭДС индукции. Закон ЭМИ для проводящего контура выглядит: , где знак «-« соответствует правилу Ленца. Ток в этом случае называется индукционным. По закону Ома выражение для тока индукции : 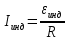, где R – сопротивление контура.

    Если имеется замкнутый контур с переменным током, тогда магнитное поле с изменяющимся потоком создается собственным током в этом контуре, и в соответствии с законом ЭМИ в контуре возникает дополнительная ЭДС, называемая ЭДС самоиндукции. Явлением самоиндукции называется возникновение ЭДС индукции при протекании по самому проводнику переменного тока. Закон самоиндукции:

    Эспериментальная часть:

    В данной лабораторной работе используется компьютерная модель, в которой изменяющийся магнитный поток возникает в результате движения проводящей перемычки по параллельным проводникам, подключенным к цепи с одной стороны.



    Проводящая перемычка движется со скоростью по параллельным проводам, замкнутым с одной стороны. Система проводника расположена в однородном магнитном поле, индукция которого направлена перпендикулярно плоскости, в которой расположены проводники. Получим формулу для индукционного тока по модулю в данном случае: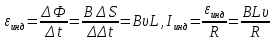

    Для бригады №1: R=1 Ом, В1=-30 мТл, В2=40мТл, В3=90мТл, L=1м.

    Для B1=-30 мТл

    υ=, м/с

    -10
    -8
    -6
    -4
    -2
    0
    2
    4
    6
    8
    10

    ЭДС,В
    -0,3
    -0,24
    -0,18
    -0,12
    -0,06
    0
    0,06
    0,12
    0,18
    0,24
    0,3

    I, мА
    -300
    -240
    -180
    -120
    -60
    0
    60
    120
    180
    240
    300

    Для B1=40 мТл

    υ=, м/с

    -10
    -8
    -6
    -4
    -2
    0
    2
    4
    6
    8
    10

    ЭДС,В
    0,4
    0,32
    0,24
    0,16
    0,08
    0
    -0,08
    -0,16
    -0,24
    -0,32
    -0,4

    I, мА
    400
    320
    240
    160
    80
    0
    -80
    -160
    -240
    -320
    -400



    Для B1=90 мТл

    υ=, м/с

    -10
    -8
    -6
    -4
    -2
    0
    2
    4
    6
    8
    10

    ЭДС,В
    0,90
    0,72
    0,54
    0,36
    0,18
    0
    -0,18
    -0,36
    -0,54
    -0,72
    -0,90

    I, мА
    900
    720
    540
    360
    180
    0
    -180
    -360
    -540
    -720
    -900


    I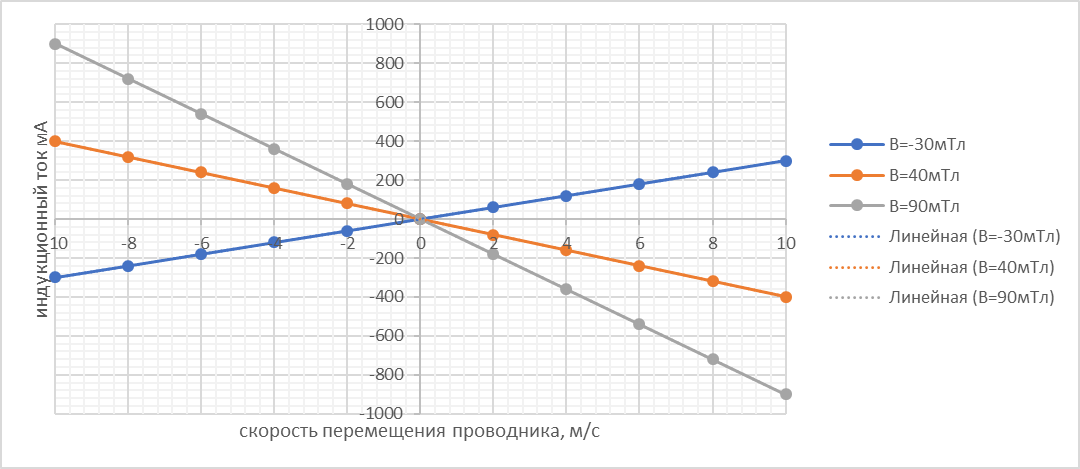
    Для каждой прямой определяем тангенс угла наклона по формуле: 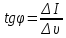, а теоретическое значение по формуле



    Номер измерения
    tgφэкс, Ас/м (по модулю)
    tgφтеор, Ас/м (по модулю)

    В=-30 мТл
    0,03
    0,03

    В= 40мТл
    0,04
    0,04

    В=90 мТл
    0,09
    0,09


    Вывод: В данной лабораторной работе используется компьютерная модель, в которой индукционный ток возникает в проводящей перемычке, перемещающейся в магнитном поле по параллельным проводникам, подключенным к цепи с одной стороны. В ходе лабораторной работы выяснены основные закономерности явления ЭМИ: 1) при изменении направления внешнего магнитного поля – меняется направление индукционного тока в движущейся перемычке, 2) при изменении в постоянном магнитном поле направления скорости движения перемычки – меняется направление индукционного тока; 3) при увеличении скорости перемещения перемычки – увеличивается величина индукционного тока. Полученная теоретическая формула для определения ЭДС индукции, возникающей в перемычке, движущейся в однородном магнитном поле, точно определяет экспериментально полученную связь индукционного тока и скорости перемещения.

    написать администратору сайта