Лабораторная работа 2 Дискретное преобразование Фурье (дпф). Выполнил студент 506 гр. Калугарев Ф. С проверил
 Скачать 94.08 Kb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФГБОУ ВО АЛТАЙСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ Институт цифровых технологий, электроники и физики Кафедра вычислительной техники и электроники (ВТиЭ) Лабораторная работа № 2 Дискретное преобразование Фурье (ДПФ). Выполнил студент 506 гр. _______________ Калугарев Ф.С Проверил: _______________ П.Н. Уланов Лабораторная работа защищена «___»__________________2021 г. Оценка ________________ Барнаул 2021 Задание 1 Создайте сигнал, содержащий 3-5 гармоник разной частоты и амплитуды (синус или косинус). Частоты гармоник должны точно попадать в сетку частот построенного спектра, то есть должны быть кратны 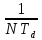 , где N – количество отсчетов сигнала. Рассчитайте ДПФ сигнала и постройте его спектр в виде гистограммы.Решение Н 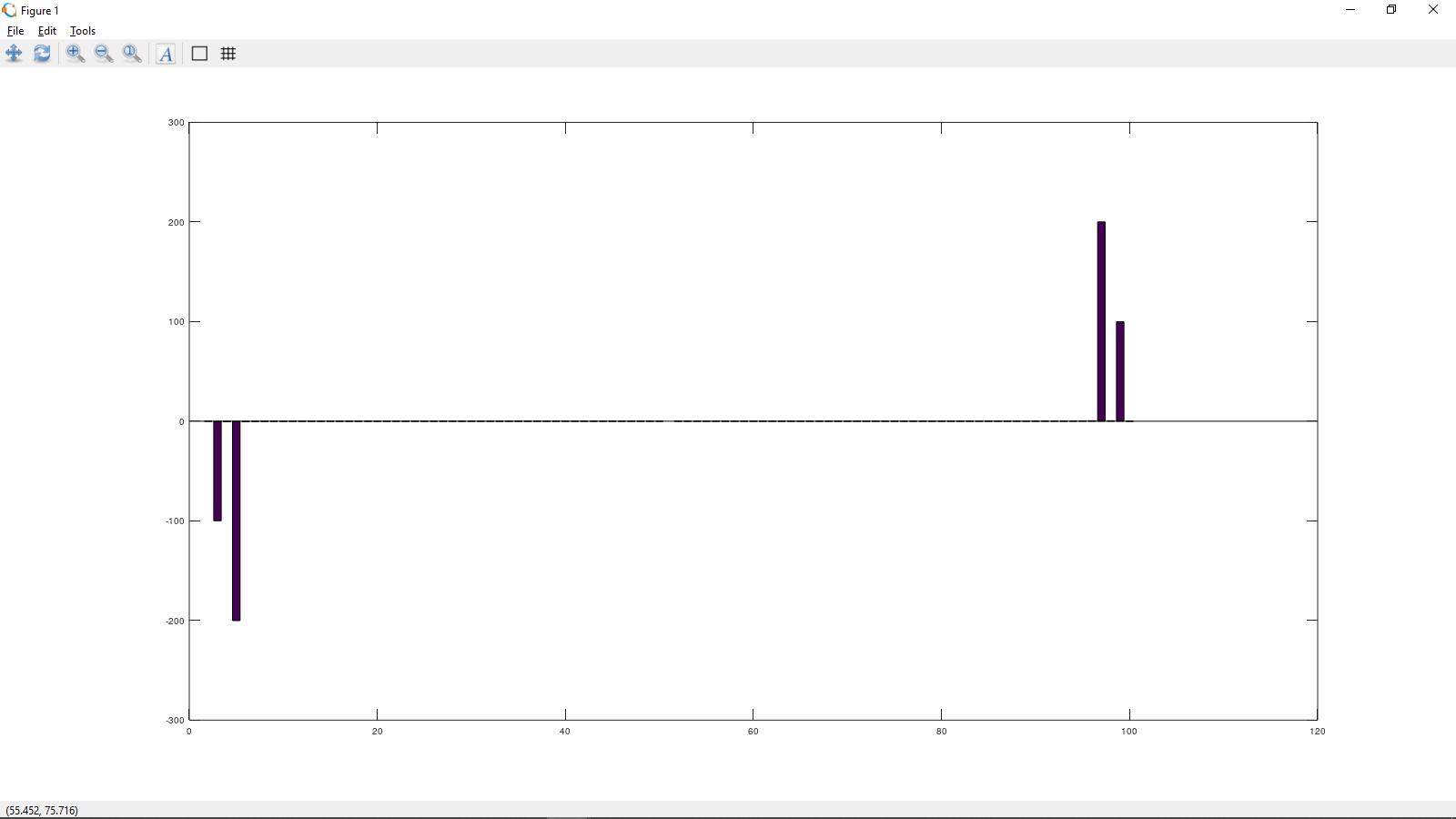 а вход программы подается сигнал . 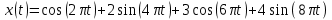Получаем распределение точек времени t на интервале [0; 0.99] с шагом 0.01. Используя функцию fft(x) в программе Octave, рассчитываем ДПФ и строим спектр в виде гистограммы. Рисунок 1. Действительная и мнимая часть По графикам видно, что у нас имеется 2 столбца, которые соответствуют действительной части гармоник, входящих в сигнал, и 2 столбца, которые соответствуют мнимой части. Задание 2 Постройте спектр одной гармоники, частота которой не кратна 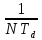.Решение На вход программы подается сигнал 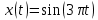 . Получаем распределение точек времени t на интервале [0; 0.99] с шагом 0.01. Используя функцию fft(x) в программе Octave, рассчитываем ДПФ и строим спектр в виде гистограммы.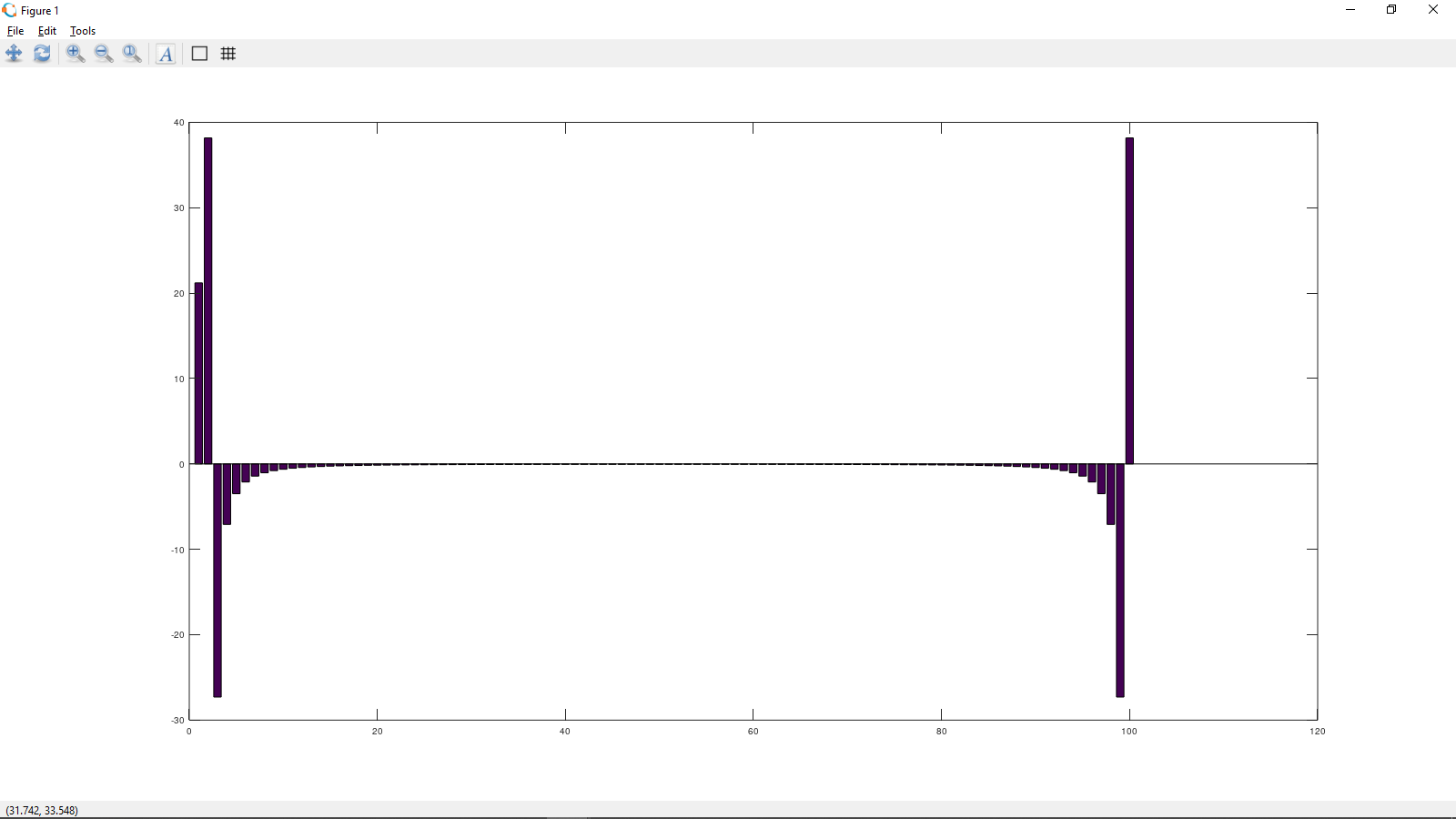 Рисунок 2 Спектр сигнала Задание 3 Рассчитайте ДПФ сигнала, заданного преподавателем. Определите номера гармоник, входящих в спектр сигнала, их амплитуду и фазу. Решение На вход программы подается заданный сигнал. Используя функцию fft(x) в программе Octave, рассчитываем ДПФ. Находим значения амплитуд гармоник, входящих в сигнал, и строим их в виде гистограммы. 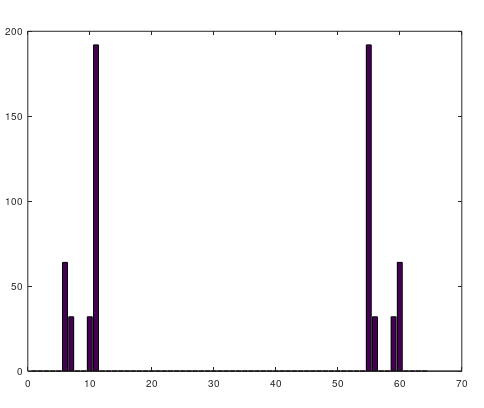 Рис. 4. Амплитуды гармоник, которые входят в сигнал. Фазу можно высчитать по формуле 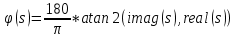 , imag(s) и reals) — мнимая и действительная части спектра соответственно.Мы получили 4 столбца, которые находятся на 6, 7, 10,11 позициях соответственно. Фаза столбца на 6-ей позиции равна 𝜑(6) = 55.7651. Фаза столбца на 7-ой позиции равна 𝜑(7) = 76.9686. Фаза столбца на 10-ой позиции равна 𝜑(10) = -162.1256. Фаза столбца на 11-ой позиции равна 𝜑(11) = -143.8313. Вывод При выполнении лабораторной работы я научился находить спектр сигнала с помощью дискретного преобразования Фурье. Приложение к заданию 1 t = 0:0.01:0.99; x = cos(2*3.14*t)+2*sin(4*3.14*t)+3*cos(6*3.14*t)+4*sin(8*3.14*t) s = fft(x) bar(real(s)) bar(imag(s)) Приложение к заданию 2 t=0:0.01:0.99; x=sin(3*pi*t); s=fft(x); bar(s) Приложение к заданию 3 s = fft(signal_07); a = abs(s); p = 180/pi*atan2(imag(s), real(s)); res = imag(s); res(:, 2) = real(s); res(:, 3) = a; res(:, 4) = p; cnt = transpose(0:1:63); res(:, 5) = cnt; res bar(a) |