Акустооптический дефлектор. АКУСТООПТИЧ. ДЕФЛЕКТОР. Лабораторная работа 2 исследование акустооптического дефлектора
 Скачать 0.75 Mb. Скачать 0.75 Mb.
|
ЛАБОРАТОРНАЯ РАБОТА № 2ИССЛЕДОВАНИЕ АКУСТООПТИЧЕСКОГО ДЕФЛЕКТОРА 1. Цель лабораторной работыОзнакомление с основными элементами интегральной оптики - акустооптическими модуляторами и дефлекторами; изучение их технических характеристик, параметров, конструктивных и технологических особенностей. 2. Домашнее задание1. Ознакомиться с теоретическим описанием работы, принципом действия, устройством, схемой включения акустооптического дефлектора (АОД) и методикой измерения его параметров и характеристик (по настоящему описанию). 2. Подготовить бланк отчета, содержащего цель работы, схему экспериментальной установки, миллиметровую бумагу с осями координат для измерения характеристик. 3. Схема лабораторной установки и описание ее элементов Блок - схема установки для измерения параметров акустооптического дефлектора типа МЛ-201 приведена на рис.1. В ней лазер и переотражающие зеркала 1 и 2, АОД, оптический поглотитель, фотоприемная матрица (ФПУ-14), 32-канальный видеоусилитель – закреплены на верхней стороне установки и в процессе работы не регулируются. ФПУ и ВУ совмещены и выполнены в виде неразъемного устройства. Лазерное излучение подается на АОД под углом Брэгга, соответствующем частоте входного сигнала равной 130 МГц. АОД типа МЛ-201 выполнен в металлическом корпусе, в котором размещен модуляционный элемент в виде звукопровода - призмы из молибдата свинца. Методом диффузионной сварки к верхней грани звукопровода прикреплен пьезопреобразователь из ниобата лития. Согласование входного импеданса пьезопреобразователя с трактом управляющего сигнала осуществляется с помощью двух катушек индуктивности Принцип действия АОД заключается в следующем. Электрическое поле, приложенное к пьезопреобразователю, возбуждает акустическую продольную волну, которая распространяется в призме - звукопроводе. Акустическая волна из-за фотоупругого эффекта вызывает изменения показателя преломления призмы. При прохождении лазерного излучения через среду с периодически возмущенным показателем преломления возникает дифракция. Интенсивность отклонения АОД лазерного излучения максимальна, если угол падения удовлетворяет условию Брэгга. 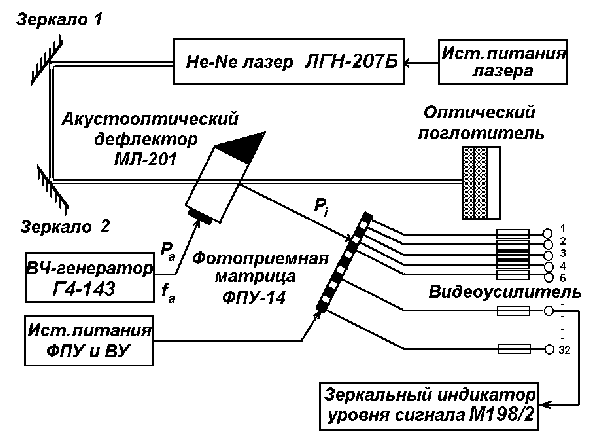 Рис.1. Блок-схема лабораторной установки. Электрическая принципиальная схема АОД приведена на рис.2. Обозначения на схеме следующие : С - конденсатор КД-1-20 пФ ± 5 %; 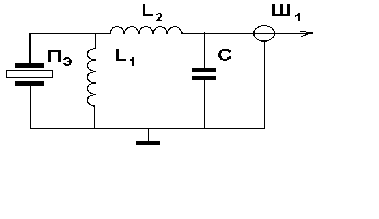 Рис.2. Принципиальная схема акустооптического дефлектора. Газовый He-Ne лазер ЛГН-207Б является одномодовым (мода ТЕМ001) источником света с круговой поляризацией, работающим в непрерывном режиме. Длина волны лазерного излучения 0,6328 мкм. Мощность лазерного излучения 1,8 мВт. Диаметр пучка лазерного излучения (на расстоянии 40 мм) 0,8 мм. Расходимость лазерного излучения 2,2 мрад. В качестве 32-канального фотоприемника используется одна фоточувствительная строка матрицы типа ФПУ-14. Строка состоит из 32 многофункциональных оптоэлектронных элементов, реализующих функции преобразования оптических непрерывных и импульсных сигналов в электрические. Каждый из 32 элементов содержит фотодиод, являющийся собственно фотоприемником, и три МДП - транзистора, на которых выполнен видеоусилитель. В целом фотоматрица ФПУ-14 представляет собой единую интегральную микросхему. Площадь фоточувствительной части ФПУ-14: 0,1 x 0,1 мм2 ; чувствительность элемента (ФПУ и ВУ) - S = 1 мкВт/мВ. 4. Порядок выполнения работыВключить питание макета: появится луч красного цвета, проходящий через оптические элементы схемы. Включить питание генератора высокой частоты типа Г4-143, нажать кнопки “ВЫХОД”,“ДИАПАЗОН-3”, установить по индикатору максимальный уровень сигнала; убедиться в том, что при плавном изменении частоты происходит перемещение дифрагированного луча по фотоприемной матрице. 4.1. Измерение амплитудно-частотной характеристики. АЧХ АОД представляет зависимость интенсивности дифрагированного света I от частоты Для определения этой зависимости штекер милливольтметра поочередно включается в выходные гнезда установки, начиная с гнезда 1 и до гнезда 32. Изменяя частоту По построенной АЧХ находится полоса частот 4.2. Измерение разрешающей способности. Включить штекер в одно из выходных гнезд, соответствующих частоте Измерения необходимо выполнить в трех-четырех точках частотного диапазона 4.3. Измерение дифракционной эффективности. Дифракционная эффективность АОД определяется отношением мощности Измерения проводятся в следующем порядке. Пользуясь приведенным экспериментальным графиком зависимости мощности Аналогичные измерения проводятся на частотах 110 и 140 МГц. 4.4. Измерение модуляционной характеристики На частоте сигнала По результатам измерений построить зависимость 5. Содержание отчета Отчет о выполнении лабораторной работы оформляется в рабочей тетради (или с помощью компьютера на листах формата А4) и должен содержать: - схему лабораторной установки; - экспериментальную АЧХ АОД в виде зависимости U = Ф ( - результаты измерений и расчета разрешающей способности АОД в трех-четырех точках частотного диапазона - результаты измерений и расчета дифракционной эффективности АОД для частот 110, 130 и 140 МГц. - экспериментальную модуляционную характеристику АОД в виде зависимости 6. Теоретическое описание работы 6.1 Возбуждение и прием акустических волн В большинстве акустооптических (АО) устройств обработки радиосигналов - спектроанализаторов, частотомеров, корреляторов и др. - ввод информации и ее преобразование осуществляется с помощью модуляторов (АОМ) и дефлекторов (АОД). В основе принципа их работы лежит явление дифракции света на ультразвуковых волнах. В зависимости от частоты акустические волны принято называть ультразвуковыми или гиперзвуковыми. Гиперзвуковые колебания - это упругие волны СBЧ диапазона, которые вплоть до 5-10 ГГц, имеют сравнительно небольшое затухание в кристаллах даже при комнатных температурах. Особенностью акустических волн является их меньшая, по сравнению с электромагнитными волнами, скорость распространения: 103 ... 104 м/с. Процесс распространения плоской монохроматической волны в твердом теле или кристалле может быть записан в виде где В зависимости от ориентации вектора смещения Для возбуждения и приема акустических волн в твердых телах чаще всего используется пьезоэлектрическая связь упругих деформаций где Рассмотрим резонансный пьезопреобразователь, представляющий собой пластину из пьезоэлектрического материала толщиной d = pL/2, где р = 1, 3, 5,... (рис.3). 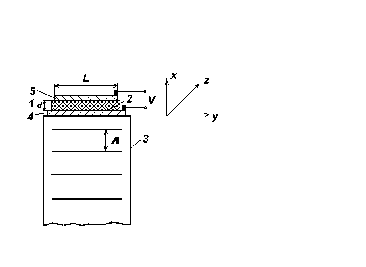 Рис.3. Резонансный пьезопреобразователь. Пластинка 1 приклеивается с помощью акустической связки 2 к звукопроводу 3, на который нанесен металлический подслой 4, являющийся электродом. Для расширения полосы рабочих частот на пьезопластинку помещается тыльная нагрузка 5, служащая одновременно вторым электродом. Малая толщина пластинки обеспечивает большую напряженность электрического поля E=V/d, где V - напряжение электрического сигнала, подводимого к электродам преобразователя, и соответственно, большую амплитуду упругих деформаций Максимальную эффективность и широкополосность имеют полуволновые преобразователи (p = l, d = L/2). При этом пьезопластинка является нагруженной резонансной системой с высокой добротностью, механические колебания пластинки 1 передаются в звукопровод 3, возбуждая в нем бегущую акустическую волну. Основной недостаток пластинчатых резонансных пьезопреобразователей обусловлен их технологической сложностью изготовления для СВЧ. Поверхностное возбуждение упругих волн осуществляется в звукопроводах из пьезоэлектрического материала. Возбуждающее электрическое поле создается в этом случае непосредственно на поверхности пьезокристалла с помощью электродных структур, замедляющих систем или СВЧ - резонаторов [ l ]. На рис. 4 изображен щелевой пьезопреобразователь из двух металлических электродов 1 и 2, нанесенных на поверхность возбуждения 4 звукопровода. Ширина щели L выбирается из условия обеспечения требуемой дифракционной расходимости звука dq@ L/L; обычно L ³ 10L. Щелевые преобразователи применяются на частотах выше 600 МГц, т.е. размер L составляет 20...100 мкм, что обеспечивает сравнительно большую напряженность электрического поля и, следовательно, большую амплитуду упругих деформаций. 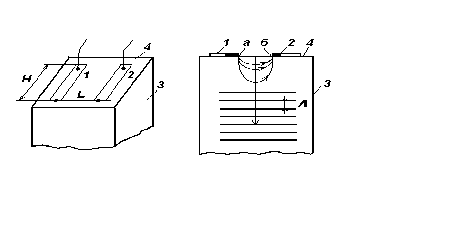 Рис. 4. Щелевой пьезопреобразователь. В щелевом преобразователе максимальная напряженность поля создается на краях электродов ( в точках "а" и "б"), поэтому его можно представить в виде двух линейных источников. Как правило, ориентация звукопровода выбирается таким образом, чтобы акустические волны возбуждались тангенциальными к поверхности возбуждения 4 компонентами электрического поля. В этом случае диаграмма направленности щелевого преобразователя будет иметь главный лепесток, направленный по нормали к поверхности 4. Пьезопреобразователи могут работать не только на передачу, но и на прием, преобразуя акустические колебания в электрический сигнал. Эффективность прямого преобразования Апр определяется отношением мощности возбуждаемой акустической волны к подводимой электрической мощности и выражается в децибеллах. Эффективность обратного преобразования также равна Апр. Для обеспечения максимального Апр в некоторой рабочей полосе частот Dfпр применяют электрическое согласование пьезопреобразователя с подводящей линией передачи [2]. Согласованные резонансные преобразователи обычно имеют эффективность Апр от -12 дБ до -3 дБ при полосах рабочих частот Dfпр = 30...400 МГц. Поверхностное возбуждение является широкополосным. В полосе частот Dfпр = 500...1500 МГц щелевой преобразователь может обеспечить потери в пределах 12...20 дБ. 6.2 Дифракция света на объемных акустических волнах Физическая картина дифракции света на упругих волнах может быть описана следующим образом. Распространение акустической волны в оптической среде сопровождается появлением бегущей периодической последовательности изменений показателя преломления. Если период этой последовательности меньше ширины светового пучка, то в среде происходит дифракция света на бегущей со скоростью звука фазовой дифракционной решетке. Характер дифракции зависит от длины области взаимодействия света и звука L. При малой величине L решетка может рассматриваться как плоская. В этом случае направления на дифракционные максимумы определяются как в обычной дифракционной решетке: где Qр - направление на р-й дифракционный максимум (р=0±1,±2...); Q0 - угол падения света; n - показатель преломления; l - длина волны света. При малом значении L дифракционная картина представляет собой набор значительного числа дифракционных максимумов, расположенных симметрично относительно направления падающего света (рис.5). Такая дифракция называется дифракцией Рамана-Ната и происходит при любом угле падения света на ультразвуковой столб. При этом можно считать, что световой луч проходит через область взаимодействия прямолинейно. 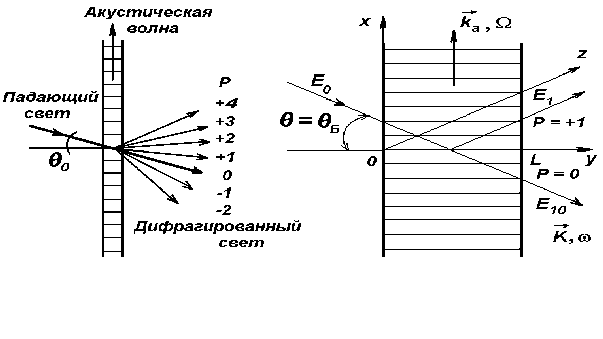 Рис. 5. Распространение акустической волны в дифракционной решетке. Иной характер носит взаимодействие света и ультразвука при большой величине L. Наведенная звуком решетка в этом случае является трехмерной и дифракция подобна дифракции рентгеновских лучей на кристаллической структуре. Такая дифракция происходит только при определенном угле падения света на ультразвуковой столб, удовлетворяющем так называемому условию Брэгга: sin(QБ)=l/2nL, и для нее характерно наличие только одного бокового дифракционного максимума. Угол падения световой волны QБ называется углом Брэгга. Режимы дифракции Рамана-Ната и Брэгга представляют собой два предельных случая, соответствующих малой и большой длине L области взаимодействия света и звука. Критерием, разграничивающим дифракции Рамана-Ната и Брэгга, является величина волнового параметра Q = 2pLl/L2. При Q << 1 имеет место дифракция Рамана-Ната, а при Q >> 1 - дифракция Брэгга. На частотах выше 100 МГц практически всегда реализуется дифракция Брэгга. При этом в случае монохроматического сигнала, возбуждающего акустическую волну, световое поле на выходе АОД состоит из двух волн - прошедшей (нулевой порядок), совпадающей по направлению распространения, частоте и поляризации с падающей на АОД, и дифрагированной (1 порядок) волны. Для рассмотрения дифракции Брэгга воспользуемся квантово- механическим подходом. Пусть плоская электромагнитная волна с частотой wп и волновым вектором в результате взаимодействия рождается фотон с энергией Учитывая, что Последнее равенство означает, что при изображении векторной диаграммы согласно соотношению (2), концы векторов 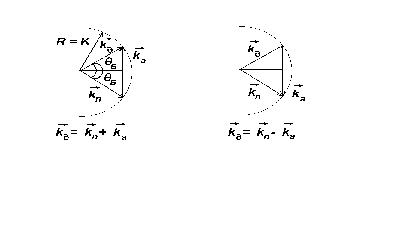 Рис. 6. Векторная диаграмма соотношения (2). Вектор 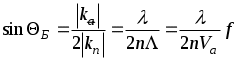 (4) (4)где Заметим, что в случае плоских волн, если направление вектора Из выражения (2) следует, что частота дифрагированного света сдвигается на частоту акустической волны. Этот сдвиг можно истолковать как допплеровский, возникающий из-за движения упругой волны относительно падающей световой. Рассчитаем интенсивность дифрагированного света на выходе АОД для обоих режимов дифракции. Пусть в изотропном звукопроводе вдоль оси x (рис.5) распространяется бегущая акустическая волна, ограниченная размером L по оси y. Акустическая волна вызывает периодическое изменение диэлектрической проницаемости среды звукопровода e- по закону где eо - проницаемость среды в отсутствие акустического поля, Далее будем считать, что угол падения света Q отличен от угла Брэгга. Взаимодействие света и звука в теле звукопровода описывается уравнениями Максвелла, от которых можно перейти к волновому уравнению для электрического поля в среде с возмущенной диэлектрической проницаемостью: Решение уравнения (6) можно искать с учетом (5) в виде совокупности плоских волн, распространяющихся в направлении дифракционных максимумов [2]: где Eр(y)- амплитуда дифракционного максимума p-го порядка с частотой w+рW. СчитаяEр(y)- медленно меняющейся функцией координаты и подставляя (7) в (6), получим для разных р систему где Можно показать, что при Q = 2pLl/L2 << 1, уравнение (8) имеет вид [2]: 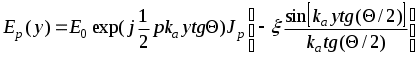 (9) (9)где При y = L в режиме Рамана-Ната получаем где При дифракции Брэгга полями всех дифракционных порядков кроме первого и нулевого можно пренебречь, т.е. считать, что в среде распространяются две волны: падающая Ео(y) и дифрагированная Е1(y). В этом случае (7) сведется к виду 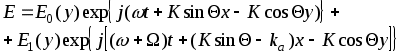 (10) (10)а система уравнений (8) к двум уравнениям где Уравнения (11) и (12) называются уравнениями связанных волн. В отсутствии акустического возмущения они становятся независимыми. При граничных условиях 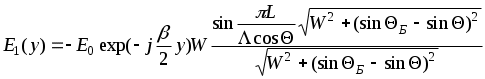 , (13) , (13)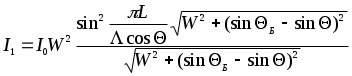 . (14) . (14)Здесь Если свет падает под углом Интенсивность света в нулевом максимуме I10 можно определить из решения (11) и (12) или из равенства I10=I0 - I1. Последнее соотношение идентично практически более удобномуР10=Р0 - Р1, где Р0, Р1, Р10 - мощности соответственно падающего, продифрагировавшего и прошедшего света. Выражение (15) показывает, что I1 возрастает по мере увеличения длины взаимодействия L, в то время как уменьшается интенсивность света I10. В практике расчетов характеристик АОД соотношение (15) применяют в виде где справедливой для случая работы АОД в условиях слабого АО взаимодействия, когда Отношение В свою очередь зависимость К числу важнейших параметров АОД, помимо эффективности дифракции, относится также полоса рабочих частот Df и разрешающая способность N. Под разрешающей способностью понимают число разрешимых в пространстве световых позиций (пятен) N , которое обеспечивает АОД при изменении частоты акустического поля в пределах Df. В свою очередь выше отмечалось, что Df АО взаимодействия имеет конечное значение из-за естественной расходимости света и звука. Вначале рассчитаем Df АОД, в котором используется оптический пучок шириной D с углом расходимости Da=l/D и узкий акустический пучок с углом расхождения DФ=L/L, причем DФ >>Da. При изменении частоты ультразвука в пределах Df углы падения и дифракции изменяются на величину При постоянном угле падения светового пучка условие Брэгга (4) может выполняться в диапазоне частот, соответствующем разрешенным значениям Приравнивая Разрешающая способность АОД определяется в первую очередь отношением угловой ширины акустического пучка DФ к ширине оптического луча Da. При изменении частоты на Df соответствующее изменение угла отклонения есть Если Df определяется только расхождением акустического пучка, то получим Принимая во внимание, что время распространения звука в звукопроводе АОД и, соответственно, время перемещения луча света равно где Dfр - частотное разрешение АОД [2], получим соотношение, связывающее быстродействие АОД и разрешающую способность N в виде 7. Контрольные вопросы 1. На основе использования каких эффектов осуществляется модуляция и отклонение оптического излучения ? 2. Каково устройство АО дефлекторов на основе изотропной дифракции ? 3. Какие существуют методы возбуждения ультразвука в твердых телах ? 4. Каковы конструктивные особенности устройств возбуждения ультразвука в твердых телах ? 5. Основные параметры АО дефлекторов. 6. Нелинейные искажения в АО дефлекторах. 7. Какие параметры влияют на эффективность и разрешающую способность АО дефлекторов ? 8. Особенности режимов дифракции Рамана-Ната и Брэгга. 9. Области применения АО дефлекторов в технике связи и технике обработки информации. 10. Особенности АО управления световыми лазерными потоками большой мощности. 8. Литература Мустель Е.Р., Парыгин В. И. Методы модуляции и сканирования света.- М.: Наука, 1970. 2. Магдич Л.Н., Молчанов В.Я. Акустооптические устройства и их применение.- М.: Сов.радио, 1978. 3. Балакший В.И., Парыгин В.Н.,Чирков Л.Е. Физические основы акустооптики.-М.: Радио и связь, 1985. 4. Малышев В.А. Элементы когерентной оптоэлектроники. Учебное пособие.- Таганрог: ТРТИ, 1988. |
