Главная страница
Навигация по странице:

  • Порядок выполнения работы

    		•

    Лабораторная ТАУ. ТАУ лр2_линейные. Лабораторная работа 2 Исследование временных характеристик типовых динамических звеньев и их соединений


    Скачать 0.68 Mb.
    НазваниеЛабораторная работа 2 Исследование временных характеристик типовых динамических звеньев и их соединений
    АнкорЛабораторная ТАУ
    Дата13.10.2022
    Размер0.68 Mb.
    Формат файлаdoc
    Имя файлаТАУ лр2_линейные.doc
    ТипЛабораторная работа
    #731331

    Лабораторная работа №2


    Исследование временных характеристик типовых динамических звеньев и их соединений
    Цель работы: изучение методики экспериментального определения временных характеристик типовых динамических звеньев и их соединений.
    В таблице 1 приведены передаточные функции основных типовых звеньев. Под типовым звеном понимается такое звено, которое описывается дифференциальным уравнением не выше второго порядка.

    Таблица 1– Типовые звенья

    №
    Тип звена
    Передаточная функция

    1
    Позиционные
    Безынерционное


    2
    Апериодическое 1-го порядка


    3
    Апериодическое 2-го порядка


    4
    Колебательное


    5
    Консервативное


    6
    Интегрирующие
    Идеальное интегрирующее


    7
    Интегрирующее с замедлением


    8
    Изодромное


    9
    Дифференцирующие
    Идеальное дифференцирующее


    10
    Дифференцирующее с замедлением


    11
    Форсирующее


    12



    Звено с запаздыванием



    Порядок выполнения работы:
    1.Запускаем Scilab и входим в среду моделирования инженерных приложений Xcos
    2.В соответствии с вариантом 1 (см. табл.2) вводим передаточные функции типовых динамических звеньев и их соединений они показаны на рисунках 1 – 5
    Таблица 2


    № варианта
    W1(S)
    W2(S)
    W3(S)
    W4(S)
    W5(S)

    интегрирующее
    Апер. 1-го порядка
    колебательное
    Апер. 2-го порядка
    Соединение

    1
    K=1
    K=1

    T=0.8
    K=1

    T=0.2

    D=0.2
    K1=1

    T1=0.2

    K2=0.5

    T2=0.5
    (10S+1)(0.1S+1)

    S(S^2+0.1S+1)


    Создаем интегрирующее и апериодическое звено первого порядка с Т = 0,8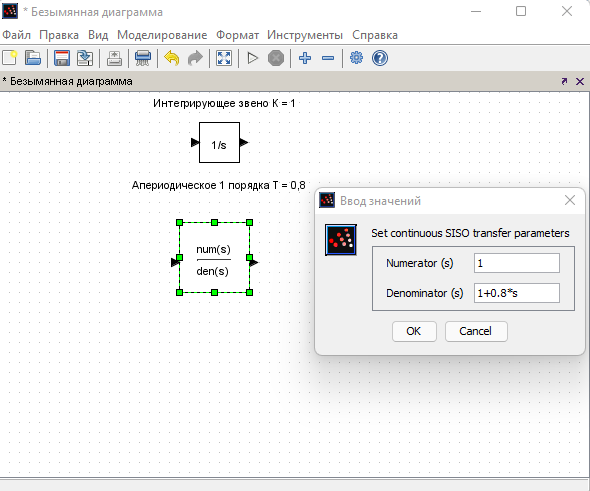


    Создаем колебательное звено с К = 1, ξ = 0.2 и Т = 0.2: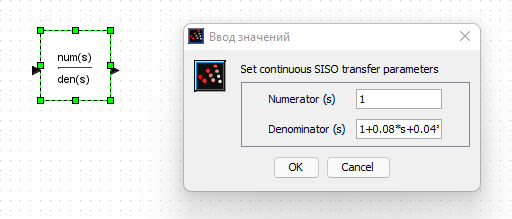


    Создаем апериодическое звено 2 порядка с параметрами с К = 0,1 Т1 = 0,2, К2 = 0,2 и Т2 = 0,5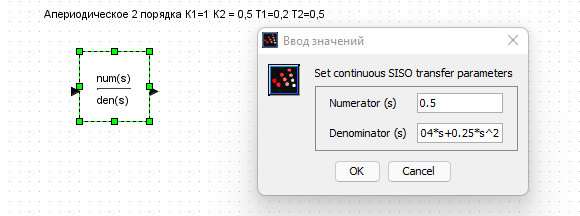


    Создаем соединение звеньев: в него входят форсирующие звенья: W1 = 10*s+1,W2 = 0.1s+1; идеальное интегрирующее звено W3 = 1/s; а также колебательное звено W4 = 1 / (s^2 + 0.1s + 1). Выражения запишем в виде полиномов перемножив соответствующие функции числителя и знаменателя: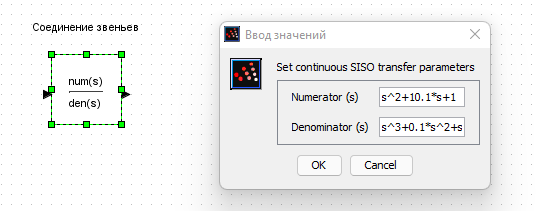


    3. Подаем на вход звена единичный ступенчатый сигнал, и пронаблюдаем переходный процесс на выходе звена, который будет являться его переходной характеристикой. Построим схемы звеньев приведенных в табл.1 с единичной отрицательной обратной связью. Приводим графики звена без обратной связи и с обратной связью на одной оси.
    Переходные характеристики звеньев без обратной связи:

    Характеристика интегрирующего звена:


    Характеристика апериодического звена 1 порядка: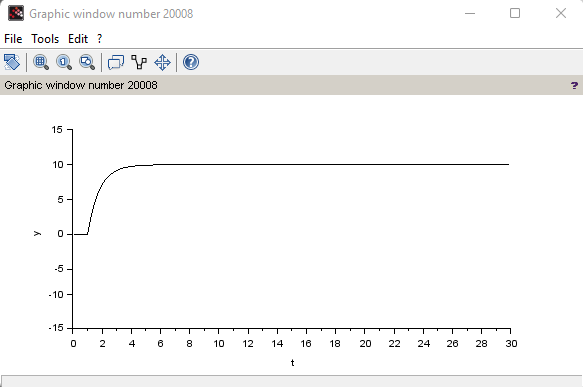


    Характеристика колебательного звена: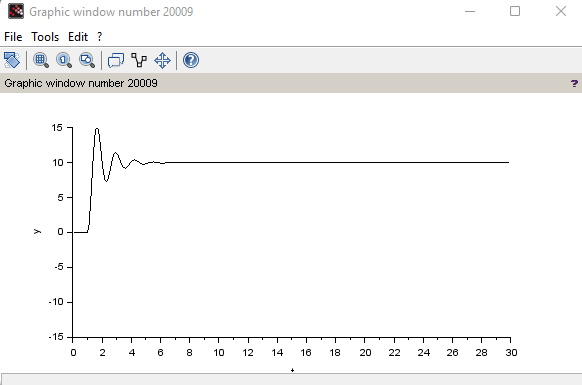


    Характеристика апериодического звена 2 порядка: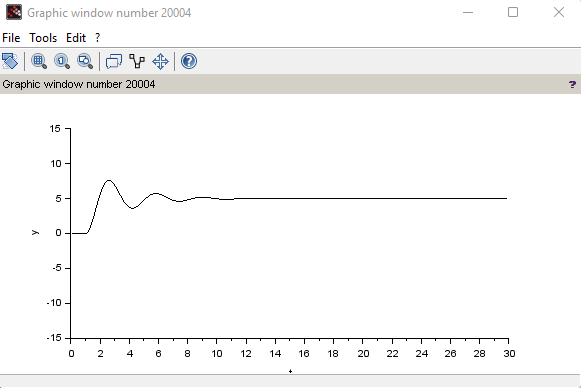


    Характеристика соединения звеньев: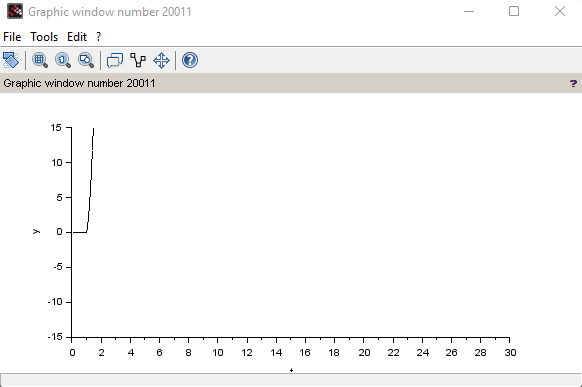

    Характеристики звеньев при наличии обратной связи:




    На графиках зеленым цветом обозначена переходная характеристика исходного звена, а черным – звена с обратной связью.

    Характеристика интегрирующего звена: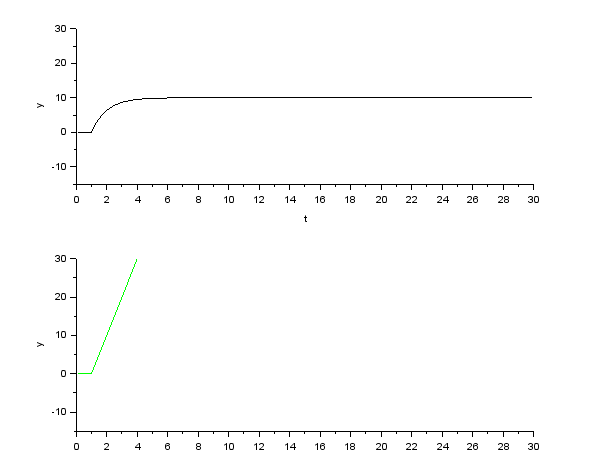


    Характеристика апериодического звена 1 порядка: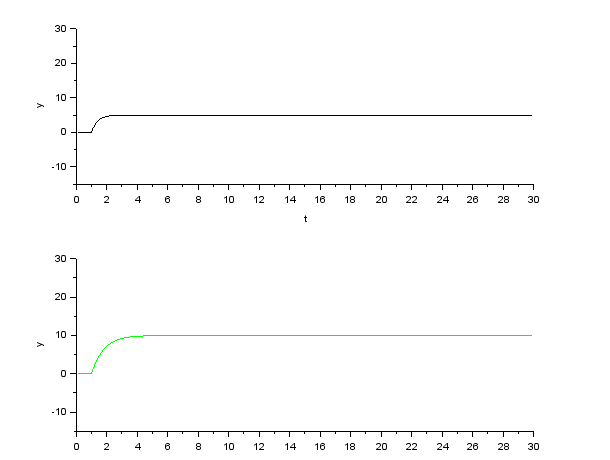

    Характеристика колебательного звена: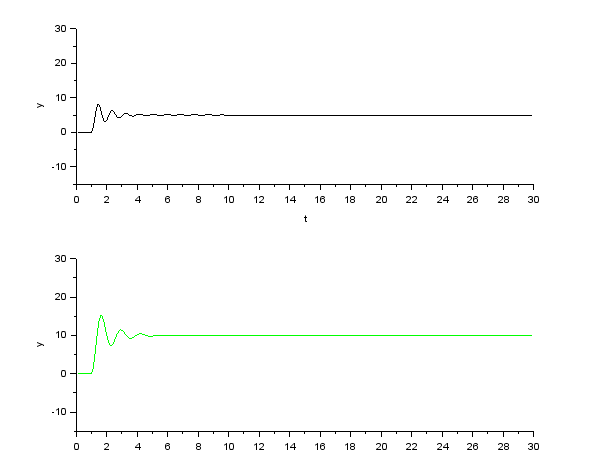

    Характеристика апериодического звена 2 порядка: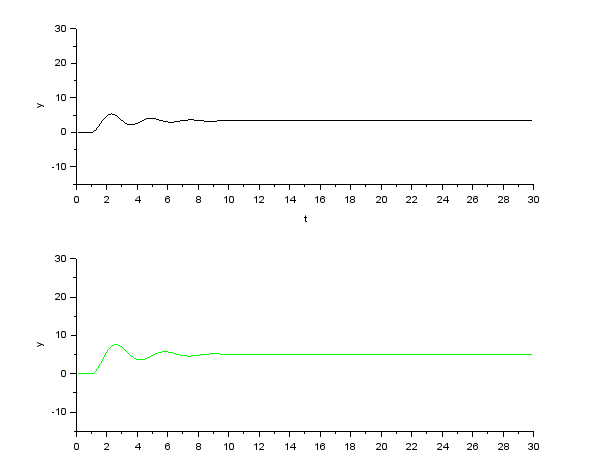


    Характеристика соединения звеньев: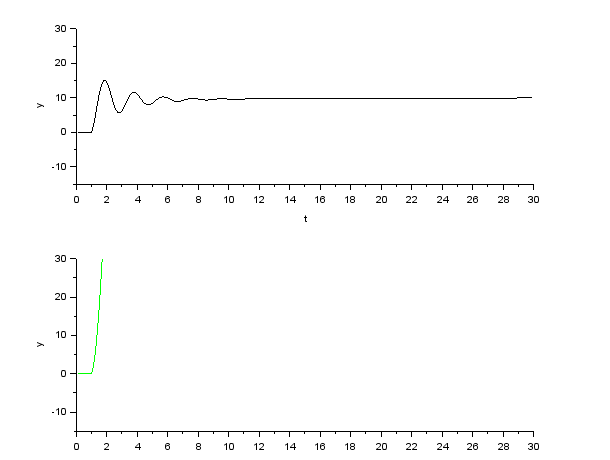


    4.Рассчитаем и введем передаточные функции колебательного звена (без обратной связи) для параметра демпфирования D1=2D и отдельно для параметра Т1=2Т. Построим на одном графике 3 вида переходной характеристики звена.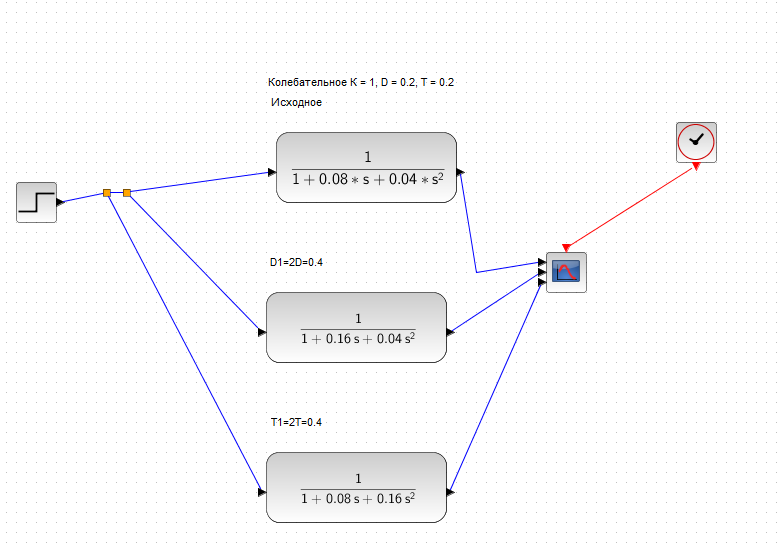

    Графики передаточных функций соответствующих звеньев приведены на рисунке: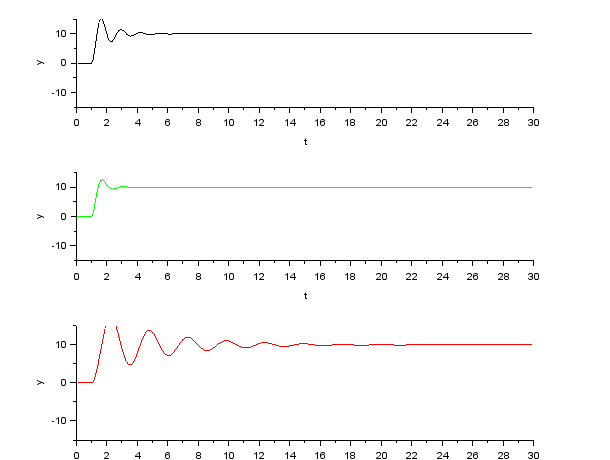

    5.Оценить влияние параметров системы (k, T, D) на характер переходной функции.
    Как видно из графика увеличение параметра D (коэффициента демпфирования) уменьшает длительность переходного процесса, увеличение параметра Т приводит к повышению длительности переходного процесса, а также к увеличению амплитудных значений. При этом коэффициент усиления влияет только на амплитудные значения.

    написать администратору сайта