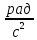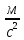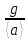Лабораторная работа по Физике уровень университет. Лабораторная работа 2 Изучение законов вращательного движения Выполнили студенты группы итссо201 Леканов Д. С
 Скачать 1.23 Mb. Скачать 1.23 Mb.
|
|
Министерство образования и науки РФ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Ульяновский государственный университет» Факультет математики, информационных и авиационных технологи Отчёт по дисциплине: «Физика» Лабораторная работа №2 Изучение законов вращательного движения Выполнили: студенты группы ИТСС-О-20/1 Леканов Д.С. _______ «___» _______ 2020 г. (подпись) (дата) Проверил: руководитель работы, старший преподаватель Богданова Д.А. _______ «___» _______ 2020 г. (подпись) (дата)  Ульяновск, 2020 г. Цель работы: изучение законов динамики вращательного движения, проверка теоремы Гюйгенса- Штайнера, оценка влияния трения на точность результатов проведенных измерений. Приборы и принадлежности: лабораторная установка «Маятник Обербека», штангенциркуль. Материал для изучения: уравнение динамики вращательного движения, момент инерции, теорема Гюйгенса-Штайнера. Основные понятия, определения и законы. Абсолютно твёрдое тело (АТТ) – тело, которое ни при каких условиях не может деформироваться, и расстояние между любыми двумя его точками остаётся неизменным. Вращательное движение твёрдого тела – механическое движение, при котором все точки тела движутся по круговым траекториям. При вращении АТТ вокруг неподвижной оси все его точки движутся по окружностям, лежащим в параллельных плоскостях. Прямая, соединяющая центры этих окружностей, называется осью вращения.
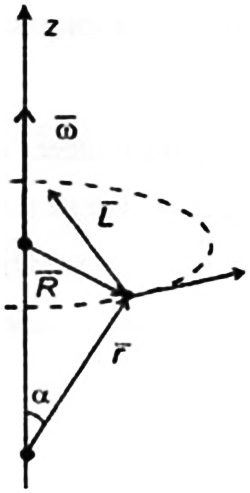
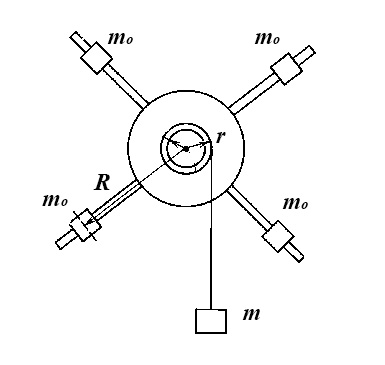
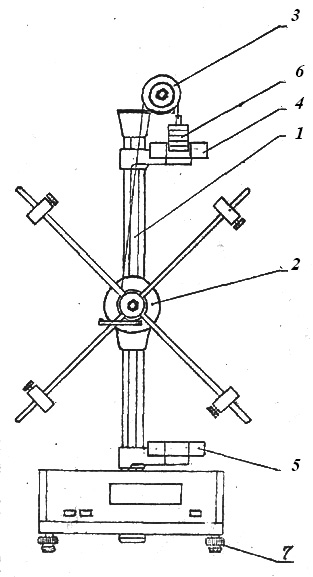
Угловая скорость 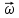 – это квазивекторная физическая величина, численно равная скорости изменения угла поворота – это квазивекторная физическая величина, численно равная скорости изменения угла поворота 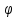 и направленная перпендикулярно плоскости вращения по правилу правого винта. и направленная перпендикулярно плоскости вращения по правилу правого винта.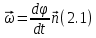 Связь линейной и угловой скорости движения материальной точки при вращательном движении: 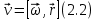 Угловое ускорение – физическая величина, равная скорости изменения угловой скорости. 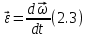 Момент импульса – физическая величина, равная векторному произведению радиус-вектора на вектор импульса ( 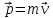 ). ).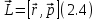 Момент силы – физическая величина, равная векторному произведению радиус-вектора на вектор силы. 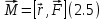 Момент инерции твёрдого тела (I) – это мера инертности твёрдого тела при его вращательном движении. Момент инерции определяется как массой тела, так и распределением массы в нём. Для системы материальных точек, вращающихся вокруг оси z: 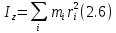 где 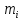 – масса материальной точки i, – масса материальной точки i, 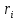 – расстояние от точки до оси z. – расстояние от точки до оси z.Для сплошного твёрдого тела, вращающегося вокруг оси z: 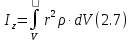 где V – объём тела, 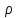 - его плотность, которая, в обще случаем, может быть функцией от координат. - его плотность, которая, в обще случаем, может быть функцией от координат.Основное уравнение динамики вращательного движения 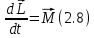 читается как: скорость изменения момента импульса тела равна результирующему моменту всех сил, действующих на тело. Для тела с постоянным моментом инерции, вращающегося вокруг оси z, основное уравнение динамики вращательного движения можно переписать в виде 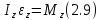 где 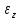 и и  – проекции углового ускорения и момента сил на ось вращения. – проекции углового ускорения и момента сил на ось вращения.Закон изменения момента импульса: скорость изменения момента импульса системы тел равна результирующему моменту всех внешних сил, действующих на систему: 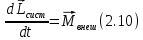 Закон сохранения момента импульса: момент импульса системы остаётся неизменным, если на систему не действуют внешние силы или моменты этих сил полностью скомпенсированы. Если необходимо установить момент инерции при вращении относительно оси z' при известном моменте инерции относительно оси z (оси z и z’параллельны, а ось zпроходит через центр масс твердого тела), то удобно применить теорему Гюйгенса-Штейнера: 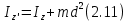 где 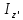 - момент инерции тела относительно оси z', - момент инерции тела относительно оси z', 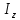 - момент инерции тела относительно оси z, - момент инерции тела относительно оси z, 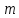 – масса тела, – масса тела, 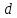 - расстояние между осями. - расстояние между осями.Центр тяжести (центр масс) системы Nматериальных точек определяется как: 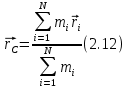 Центр тяжести (центр масс) твёрдого тела: 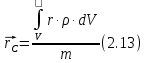 где V – объём тела, 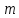 – его масса, – его масса, 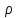 - его плотность, которая, в общем случае, может быть функцией от координат. - его плотность, которая, в общем случае, может быть функцией от координат.Методика измерений и основные расчётные формулы. На рисунке 2.2 схематически показан маятник Обербека. Четыре спицы укреплены на втулке под прямым углом. На спицах находятся грузы массой 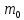 каждый. Втулка и двухступенчатый блок с радиусами каждый. Втулка и двухступенчатый блок с радиусами 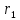 и и 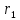 насажены на общую ось. Ось закреплена в подшипниках, так что вся система может вращаться вокруг горизонтальной оси. Передвигая грузы по спицам, можно легко изменять момент инерции I тела. На блок намотана нить, к которой привязывается груз массы m, которую можно менять с помощью съёмных колец. насажены на общую ось. Ось закреплена в подшипниках, так что вся система может вращаться вокруг горизонтальной оси. Передвигая грузы по спицам, можно легко изменять момент инерции I тела. На блок намотана нить, к которой привязывается груз массы m, которую можно менять с помощью съёмных колец. Когда груз массы m приходит в движение, он натягивает нить, и за счёт момента силы натяжения нити,Tr, блок маятника начинает вращаться.
Основное уравнение динамики вращательного движения для маятника: 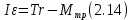 где 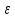 – угловое ускорение маятника, Т – сила натяжения нити, – угловое ускорение маятника, Т – сила натяжения нити, 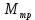 – момент силы трения, – момент силы трения, 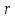 - радиус блока маятника (той его ступени, на которую намотана нить). - радиус блока маятника (той его ступени, на которую намотана нить).Второй закон Ньютона для опускающегося на нити груза: 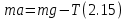 Связь линейного ускорения опускающегося груза и углового ускорения маятника: 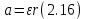 Из формул (2.14), (2.15) и (2.16) следует, что 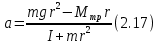 По теореме Гюйгенса-Штейнера для маятника с четырьмя спицами: 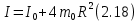 где R– расстояние от грузов 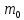 до оси вращения маятника, до оси вращения маятника, 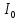 - момент инерции маятника приR=0. - момент инерции маятника приR=0.В условиях нашего эксперимента в формуле (2.17) можно пренебречь величиной 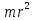 , так как она намного меньше момента инерции маятника, а также малой величиной, включающей момент силы трения. , так как она намного меньше момента инерции маятника, а также малой величиной, включающей момент силы трения.Тогда, подставив момент инерции в виде (2.18) в формулу (2.17), получаем: 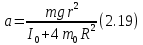 Формулу (2.19) можно преобразовать, приведя к виду удобному для экспериментальной проверки: 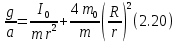 Методика измерений. Прежде чем приступить к проверке теоремы Гюйгенса-Штейнера следует экспериментально оценить момент силы трения. Из формулы (2.14) следует, что 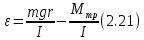 Формула (2.21) позволяет также проверить линейность зависимости углового ускорения от момента внешней силы. Для этого при постоянном моменте инерции маятника I (неизменном положении грузов на спицах) следует построить график в координатах x = 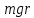 , y = , y = 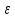 . В пределах погрешности экспериментальные точки должны ложиться на прямую. Тангенс угла наклона этой прямой равен . В пределах погрешности экспериментальные точки должны ложиться на прямую. Тангенс угла наклона этой прямой равен 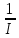 , а точка пересечения с осью абсцисс даёт , а точка пересечения с осью абсцисс даёт 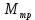 . . Если экспериментальные данные подтверждают линейную зависимость углового ускоренияот mgr,то можно приступить к проверке теоремы Гюйгенса-Штейнера. Так как при выводе формулы (2.20) мы пренебрегли моментом силы трения, в данном эксперименте массу грузаm следует выбирать такой, чтобы выполнялось неравенство: 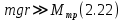 Величина 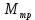 получена в ходе первого эксперимента. получена в ходе первого эксперимента. При постоянной массе груза m, формула (2.20) позволяет проверить теорему Гюйгенса-Штейнера. Для этого надо построить график в координатах x= 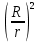 и y = и y = 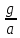 . Очевидно, что это будет линейная зависимость. . Очевидно, что это будет линейная зависимость. Ускорение 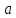 можно найти из следующих соображений. Согласно формуле (6), движение груза m – равноускоренное. Если в начальный момент времени груз начинает движение из состояния покоя, то можно найти из следующих соображений. Согласно формуле (6), движение груза m – равноускоренное. Если в начальный момент времени груз начинает движение из состояния покоя, то 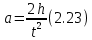 где h – расстояние пройденное грузом за времяt. Описание установки.
Практическое задание. Упражнение 1. Определите экспериментально зависимость углового ускорения маятника  от момента приложенной силы mgr.В этой серии измерений момент инерции маятника должен оставаться постоянным: I = const. В качестве rрекомендуется выбрать больший радиус (т.е. нить наматывается на ступень блока большего диаметра). от момента приложенной силы mgr.В этой серии измерений момент инерции маятника должен оставаться постоянным: I = const. В качестве rрекомендуется выбрать больший радиус (т.е. нить наматывается на ступень блока большего диаметра).Измерьте высоту h и радиус используемой ступени блока r. Эти параметры должны оставаться неизменными в течение всего эксперимента. Для определения зависимости  = f (mgr)измерьте время t, за которое груз mопускается на расстояние h. Измерение времени tдля каждого груза при постоянном значении hповторите три раза. Затем найдите среднее значение времени падения груза по формуле: = f (mgr)измерьте время t, за которое груз mопускается на расстояние h. Измерение времени tдля каждого груза при постоянном значении hповторите три раза. Затем найдите среднее значение времени падения груза по формуле: 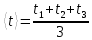 и рассчитайте среднее ускорение груза по формуле: и рассчитайте среднее ускорение груза по формуле: 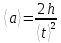 . Найдите среднее угловое ускорение по формуле: . Найдите среднее угловое ускорение по формуле: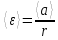 . Рассчитайте погрешности прямых измерений ( . Рассчитайте погрешности прямых измерений (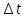 ) и косвенных измерений ( ) и косвенных измерений (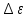 ). ).Повторите эти измерения и расчёты для пяти разных масс m. Причём все массы должны удовлетворять неравенству (2.22). Данные занесите в Таблицу 1. Таблица 1. (h = 0,31 м; R= 0,08 м ; r= 0,0335 м; )
Используя данные таблицы, построить по методу наименьших квадратов график в координатах x = 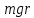 и y = и y = 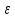 . По тангенсу угла наклона этой прямой определить . По тангенсу угла наклона этой прямой определить 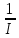 , а по точке пересечения с осью абсцисс – , а по точке пересечения с осью абсцисс – 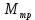 . . Погрешность высоты брать как систематическую погрешность прибора, т.е. половину цены деления шкалы. В качестве rрекомендуется выбрать радиус большей из ступеней блока. Диаметр ступени блока измеряется штангенциркулем. Упражнение 2. Проверьте экспериментально зависимость (7). Для этого, взяв постоянную массу груза т (т>>т0), определите ускорение а грузат при пяти различных положениях Rгрузов  на спицах. Для расчёта ускорения и среднего времени падения используйте те же формулы, что и в предыдущем упражнении. Рассчитайте погрешности прямых измерений ( на спицах. Для расчёта ускорения и среднего времени падения используйте те же формулы, что и в предыдущем упражнении. Рассчитайте погрешности прямых измерений ( ) и косвенных измерений ( ) и косвенных измерений ( ). ).При каждом положении грузов на спицах, R,измерения времени падения повторите три раза. Результаты измерений занесите в Таблицу 2. Погрешность высоты брать как систематическую погрешность прибора, т.е. половину цены деления шкалы. В качестве rрекомендуется выбрать радиус большей из ступеней блока. Диаметр ступени блока измеряется штангенциркулем. Таблица 2. (h = 0,31 м; r = 0,0335 м; 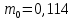 кг; кг;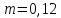 кг) кг)
По данным таблицы построить график в координатах x= 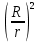 и y = и y = 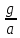 по методу наименьших квадратов. По точке пересечения получившейся прямой с осью ординат определить по методу наименьших квадратов. По точке пересечения получившейся прямой с осью ординат определить 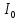 , момент инерции маятника приR=0. , момент инерции маятника приR=0.График 1) 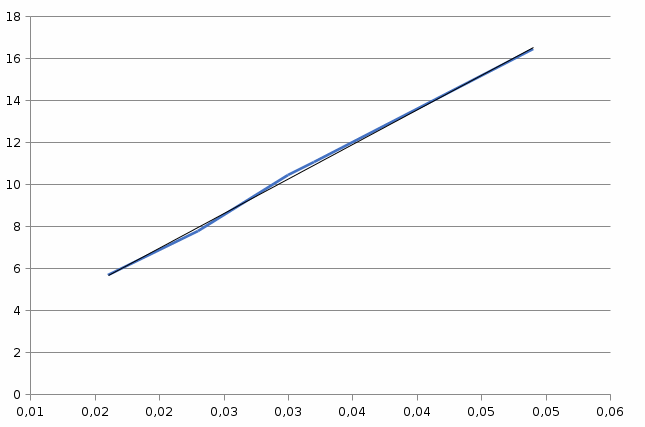 График 2) 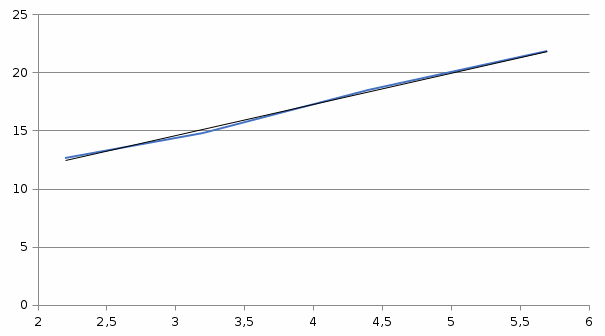   |

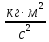
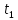 , с
, с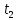 , с
, с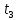 , с
, с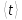 , с
, с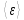 ,
,