Главная страница
Навигация по странице:

  • Лабораторная работа №2 МЕТОДЫ ИНТЕРПОЛЯЦИИ И ЭКСТРАПОЛЯЦИИ Вариант №5

  • 2.Формулы метода.

  • 3.Результаты выполнения задания в Mathcad ’ e .

  • 5.Исходный код

  • 6.Результаты выполнения работы в виде значений коэффициентов интерполирующего полинома и графика полученного полинома с нанесенными на график исходными данными

  • 7.Библиографический список

    		•

    отчёт 2. Лабораторная работа 2 методы интерполяции и экстраполяции вариант 5 Студент гр. Ут 21 Петухов П. А


    Скачать 241 Kb.
    НазваниеЛабораторная работа 2 методы интерполяции и экстраполяции вариант 5 Студент гр. Ут 21 Петухов П. А
    Анкоротчёт 2.doc
    Дата15.08.2018
    Размер241 Kb.
    Формат файлаdoc
    Имя файлаотчёт 2.doc
    ТипЛабораторная работа
    #22993


    МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

    РОССИЙСКОЙ ФЕДЕРАЦИИ

    ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ

    БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

    ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

    «ВЯТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»

    Лабораторная работа №2

    МЕТОДЫ ИНТЕРПОЛЯЦИИ И ЭКСТРАПОЛЯЦИИ

    Вариант №5

    Студент: гр. УТ – 21 Петухов П.А.

    Преподаватель: Чуркин В.В.

    Киров

    2013 год
    1.Задание.

    1) В Mathcad’е по заданному из таблицы варианту выполнить кусочно-линейную и сплайн-интерполяции для функции заданной таблицей значений в точках где .

    2) Составить алгоритм и написать код для определения параметров и построения графика интерполяционного тригонометрического многочлена. Нанести на график значения функции из таблицы

    2.Формулы метода.

    Задача тригонометрической интерполяции состоит в построении тригонометрического интерполяционного многочлена наименьшей степени удовлетворяющего условиям

    Решением этой задачи является тригонометрический многочлен:



    коэффициенты которого вычисляются по следующим формулам: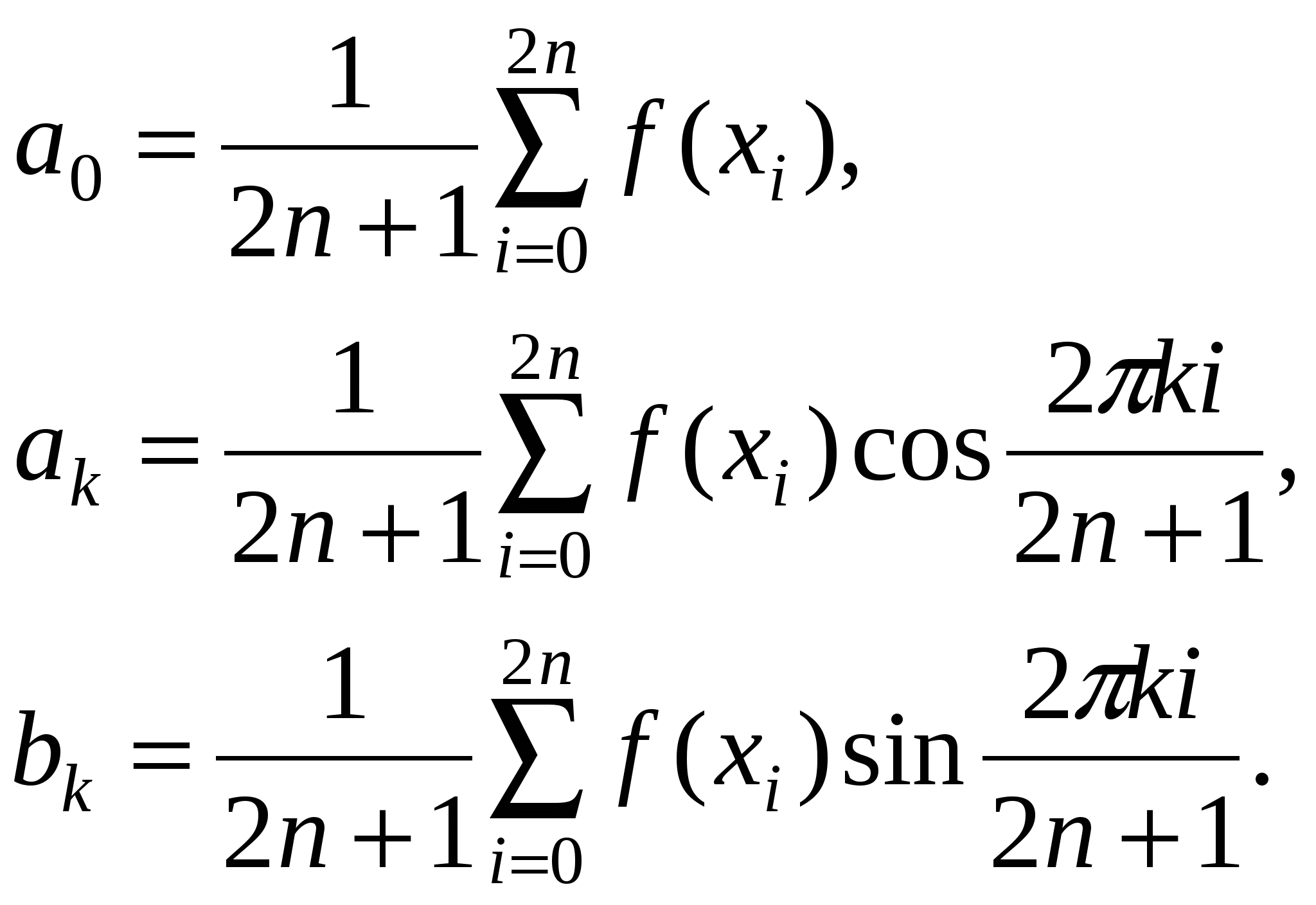


    3.Результаты выполнения задания в Mathcad’e.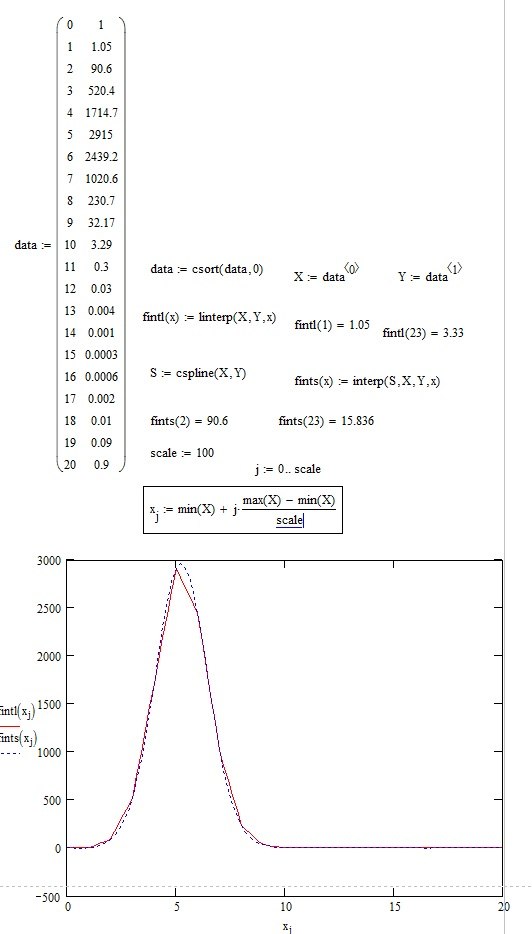



    4.1 Блок-схема алгоритма

    4.2 Таблица идентификаторов


    Имя переменной
    Тип переменной
    Диапазон
    Назначение

    Алгоритм
    Программа

    x[21]
    x[21]
    double
    От ±5.0 × 10−324 до ±1.7 × 10308
    Объявление вещественного массива

    y[21]
    y[21]
    double
    От ±5.0 × 10−324 до ±1.7 × 10308
    Объявление вещественного массива

    a[11]
    a[11]
    double
    От ±5.0 × 10−324 до ±1.7 × 10308
    Объявление вещественного массива

    b[11]
    b[11]
    double
    От ±5.0 × 10−324 до ±1.7 × 10308
    Объявление вещественного массива

    i
    i
    int
    От -2 147 483 648 до 2 147 483 647
    Переменная цикла

    k
    k
    int
    От -2 147 483 648 до 2 147 483 647
    Переменная цикла

    x[i]
    x[i]
    double
    От ±5.0 × 10−324 до ±1.7 × 10308
    Элементы массива

    y[i]
    y[i]
    double
    От ±5.0 × 10−324 до ±1.7 × 10308
    Элементы массива

    a[k]
    a[k]
    double
    От ±5.0 × 10−324 до ±1.7 × 10308
    Элементы массива

    b[k]
    b[k]
    double
    От ±5.0 × 10−324 до ±1.7 × 10308
    Элементы массива

    p
    p
    float
    От -3.4 × 1038 до 3.4 × 1038
    Результат вычислений

    x
    x
    float
    От -3.4 × 1038 до 3.4 × 1038
    Переменная цикла

    5.Исходный код

    Файл реализации «Class1.cpp»
    //---------------------------------------------------------------------------

    #pragma hdrstop

    #include "Class1.h"

    #include "string.h"

    #include "strstream.h"

    #include "Unit1.h"

    #include "Unit2.h"

    #include "Unit3.h"

    #include

    //---------------------------------------------------------------------------

    #pragma package(smart_init)

    double y[21]={1.0, 1.05, 90.6, 520.4, 1714.7, 2915.0, 2439.2, 1020.6,

    230.7, 32.17, 3.29, 0.3, 0.03,

    0.004, 0.001, 0.0003, 0.0006, 0.002, 0.01, 0.09, 0.9};

    void Class1::aboutme()

    {

    Application->MessageBox("Данное приложение выполнено студентом ВятГУ Факультета АВТ группы УТ-21 Петуховым Павлом", "О создателе" );

    }

    void Class1::koord()

    {

    Form1->StringGrid1->Cells[0][0]="i";

    Form1-> StringGrid1->Cells[0][1]="x[i]";

    Form1->StringGrid1->Cells[0][2]="y[i]";

    for(int i=0;i<21;i++){

    Form1-> StringGrid1->Cells[i+1][0]=IntToStr(i);

    x[i]=2*M_PI*i/21;

    Form1->StringGrid1->Cells[i+1][1]=FloatToStrF(x[i],ffFixed,2,2);

    Form1->StringGrid1->Cells[i+1][2]=FloatToStrF(y[i],ffFixed,2,2);}

    }

    void Class1::koeef()

    {

    for(int k=0;k<=10;k++){

    Form1->StringGrid2->Cells[0][0]="k";

    Form1->StringGrid2->Cells[0][1]="a[k]";

    Form1-> StringGrid2->Cells[0][2]="b[k]";

    Form1->StringGrid2->Cells[k+1][0]=IntToStr(k);

    a[k]=b[k]=0;

    for(int i=0;i<21;i++){

    a[k]+=StrToFloat(Form1->StringGrid1->Cells[i+1][2])*cos(k*x[i]);

    b[k]+=StrToFloat(Form1->StringGrid1->Cells[i+1][2])*sin(k*x[i]);}

    a[k]/=21;

    Form1->StringGrid2->Cells[k+1][1]=FloatToStrF(a[k],ffFixed,5,5);

    b[k]/=21;

    Form1->StringGrid2->Cells[k+1][2]=FloatToStrF(b[k],ffFixed,5,5);}

    }

    void Class1::tablica()

    {

    Form1->Series1->Clear();

    Form1->Series2->Clear();

    for(int i=0;i<21;i++){

    Form1-> Series1->AddXY(x[i],StrToFloat(Form1->StringGrid1->Cells[i+1][2]),"",clBlack); }

    for(float x=0;x<2*M_PI;x+=0.001){

    float p=a[0];

    for(int k=1;k<11;k++)

    p+=2*(a[k]*cos(k*x)+b[k]*sin(k*x));

    Form1-> Series2->AddXY(x,p,"",clBlack);}

    }

    void Class1::helpf()

    {

    Form3->Show(); //обращение к форме}

    6.Результаты выполнения работы в виде значений коэффициентов интерполирующего полинома и графика полученного полинома с нанесенными на график исходными данными



    7.Библиографический список

    В.В.ЧУРКИН ЧИСЛЕННЫЕ МЕТОДЫ (с алгоритмами и программами в среде C++Builder) Учебно-методическое пособие. 2013.

    написать администратору сайта