Главная страница
Навигация по странице:

  • Вариант a b c d

  • Корни уравнения У=0,5Х

  • Левая часть ( y ) Корни (x)

  • Левая часть Корни

    		•

    лаба. Лабораторная работа 2 по дисциплине Информационные технологии


    Скачать 0.55 Mb.
    НазваниеЛабораторная работа 2 по дисциплине Информационные технологии
    Дата21.04.2023
    Размер0.55 Mb.
    Формат файлаdocx
    Имя файлаIT_lab.docx
    ТипЛабораторная работа
    #1079073
    страница3 из 5
    1   2   3   4   5

    Упражнение 8. «Корни кубического уравнения»

    Задание. Известно, что кубическое уравнение y = aХ 3 + bX 2 + cX + d в интервале [x1 ; x2] имеет три действительных корня. Найти корни уравнения методом подбора параметра.

    ПО ВАРИАНТАМ

    Вариант
    a
    b
    c
    d
    [x1 ; x2 ]

    1
    0,5
    3
    -1
    -3
    [-7 ; 2]

    2
    0,5
    2
    -0,5
    -3
    [-4,5 ; 2]

    3
    0,5
    2
    -1
    -5
    [-5 ; 2]

    4
    0,4
    2
    -2
    -5
    [-7 ; 3]

    5
    0,4
    2
    -3
    -6
    [-7 ; 3]

    6
    -0,4
    -1
    3
    6
    [-4 ; 3]

    7
    -0,4
    -2
    3
    6
    [-7 ; 3]

    8
    0,4
    1
    -3
    -6
    [-4 ; 3]

    9
    -0,4
    -2
    2
    5
    [-7 ; 3]

    10
    -0,5
    -2
    1
    5
    [-5 ; 2]

    11
    -0,5
    -3
    1
    3
    [-7 ; 2]

    12
    -0,5
    -2
    0,5
    3
    [-4,5 ; 2]

    13
    -0,4
    -1
    3
    6
    [-4 ; 4]

    14
    0,5
    2
    -1
    -5
    [-6 ; 3]

    15
    -0,5
    -2
    1
    5
    [-6 ; 3]

    16
    -0,4
    -2
    3
    6
    [-7 ; 3]

    17
    0,4
    1
    -3
    -6
    [-4 ; 3]

    18
    -0,4
    -2
    2
    5
    [-7 ; 3]

    19
    -0,5
    -2
    1
    5
    [-5 ; 2]

    20
    -0,5
    -3
    1
    3
    [-7 ; 2]

    21
    0,5
    2
    -0,5
    -3
    [-4,5 ; 2]

    22
    0,5
    2
    -1
    -5
    [-5 ; 2]

    23
    0,4
    2
    -2
    -5
    [-7 ; 3]

    Порядок выполнения для кубического уравнения У=0,5Х3+2X2-X-3 на участке от -5 до 2.

    1. Подготовить таблицу (табл.13) .

    Таблица 13
    А

    В
    С



    Корни уравнения У=0,5Х3+2Х2-Х-3






    Левая часть (y)
    Корни (x)



    1








    2








    3








    1. В ячейке В3 вывести формулу: =0,5*C3^3+2*C3^2-C3-3

    2. С помощью маркёра заполнения продолжить эту формулу на ячейки В5, В5.

    3. Так как в задании указана область поиска от -5 до 2, то расставим начальные значения корней -5,0 и 2, через 0. Тогда исходное состояние таблицы примет вид табл. 14.

    Таблица 14
    А

    В
    С



    Корни уравнения У=0,5Х3+2Х2-Х-3






    Левая часть (y)
    Корни (x)



    1
    -10,5
    -5



    2
    -3
    0



    3
    7
    2



    1. Установить курсор в ячейке В3, вызвать диалог «Подбор параметра», заполнить бланк как на рис. 56.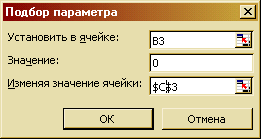



    В результате выполнения этой операции в ячейке В3 появится число, записанное в экспоненциальной форме, близкое к нулю, а в ячейке значение первого корня -4,13264.

    1. Повторить подбор параметра для ячеек В4 и В5. В результате получится табл. 14.

    Таблица 14
    Левая часть
    Корни

    1
    -3,29599E-05
    -4,1326416

    2
    -0,000197104
    -1,1403808

    3
    0,000296781
    1,2731184
    1   2   3   4   5

    написать администратору сайта