ПОКАЗАТЕЛИ ЗНАЧЕНИЙ ЦЕНТРА И РАЗМАХОВ ВАРИАЦИЙ СТАТИСТИЧЕСКОГО РАСПРЕДЕЛЕНИЯ. Лабораторная работа 2 показатели значений центра и размахов вариаций статистического распределения по дисциплине Теория вероятностей и математическая статистика
 Скачать 383.7 Kb. Скачать 383.7 Kb.
|
|
Федеральное агентство железнодорожного транспорта Сибирский государственный университет путей сообщения Кафедра « Системный анализ и управление проектами » Лабораторная работа № 2 «ПОКАЗАТЕЛИ ЗНАЧЕНИЙ ЦЕНТРА И РАЗМАХОВ ВАРИАЦИЙ СТАТИСТИЧЕСКОГО РАСПРЕДЕЛЕНИЯ» по дисциплине «Теория вероятностей и математическая статистика» Руководитель Разработал студент гр. __МЛ-212_ ________________ст.пр. _____________ (подпись) (подпись) __________________ _____________________ (дата проверки) (дата сдачи на проверку) Краткая рецензия: ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ _________________________________ (запись о допуске к защите) ________________________________ _________________________________ (оценка по результатам защиты) (подписи преподавателей) 2021 год ФГБОУ ВО СГУПС Кафедра «Системный анализ и управление проектами» Задание на выполнение лабораторной работы по дисциплине «Теория вероятностей и математическая статистика»
Тема: Показатели значений центра и размахов вариаций статистического распределения. Цель работы: Приобретение навыков обработки и обобщения индивидуальных значений одного и того же признака у различных единиц совокупности. Вариант задания: 35 График выполнения
Сроки сдачи на проверку: 10 неделя текущего семестра. Сроки защиты: 11 неделя текущего семестра. Работу оформить в соответствии со стандартом организации СТО СГУПС 1.01 БИ.01-2019 «Система менеджмента качества. Письменная отчетная работа. Требования к оформлению». Основная литература: 1) Мацкевич И.П., Свирид Г.П., Булдык Г.М. Сборник задач и упражнений по высшей математике (Теория вероятностей и математическая статистика). Минск: Вышейш. шк., 1996.  Задание выдано «15» октября 2021 г. 2) Гмурман В. Е. Теория вероятностей и математическая статистика. М.: Высш. Шк., 1977 3) Тимофеева Л.К., Суханова Е.И., Сафиулин Г.Г. Теория вероятностей и математическая статистика / Самарск. гос. экон. акад. Самара, 1994.
ОГЛАВЛЕНИЕ1 «ПОКАЗАТЕЛИ ЗНАЧЕНИЙ ЦЕНТРА И РАЗМАХОВ ВАРИАЦИЙ СТАТИСТИЧЕСКОГО РАСПРЕДЕЛЕНИЯ» 1 Введение 4 1Постановка задачи 7 2Выполнение задания 8 2.2 Медиана 10 2.3 Мода 11 2.6Дисперсия и среднеквадратическое отклонение дискретного ряда 16 2.7 Нахождение квартилей 20 2.8 Относительные показатели вариации 22 3.9 Показатель фондовой дифференциации 22 3 Вывод 24 Введение Цель работы: приобретение навыков группирования и обработки первичной статистической информации в интерактивной среде Excel. Статистическая информация — это цифровая информация в виде числовых рядов различных показателей, прогнозных моделей и оценок. Данные представлены в виде средних или относительных величин и позволяют выявлять закономерности развития социально-экономических явлений и процессов. Математическая статистика — раздел математики, разрабатывающий методы регистрации, описания и анализа данных наблюдений и экспериментов с целью построения вероятностных моделей массовых случайных явлений. В зависимости от математической природы конкретных результатов наблюдений статистика математическая делится на статистику чисел, многомерный статистический анализ, анализ функций (процессов) и временных рядов, статистику объектов нечисловой природы. Выделяют описательную статистику, теорию оценивания и теорию проверки гипотез. Описательная статистика есть совокупность эмпирических методов, используемых для визуализации и интерпретации данных (расчет выборочных характеристик, таблицы, диаграммы, графики и т. д.), как правило, не требующих предположений о вероятностной природе данных. Некоторые методы описательной статистики предполагают использование возможностей современных компьютеров. К ним относятся, в частности, кластерный анализ, нацеленный на выделение групп объектов, похожих друг на друга, и многомерное шкалирование, позволяющее наглядно представить объекты на плоскости. Методы оценивания и проверки гипотез опираются на вероятностные модели происхождения данных. Эти модели делятся на параметрические и непараметрические. В параметрических моделях предполагается, что характеристики изучаемых объектов описываются посредством распределений, зависящих от (одного или нескольких) числовых параметров. Непараметрические модели не связаны со спецификацией параметрического семейства для распределения изучаемых характеристик. В математической статистике оценивают параметры и функции от них, представляющие важные характеристики распределений (например, математическое ожидание, медиана, стандартное отклонение, квантили и др.), плотности и функции распределения и пр. Используют точечные и интервальные оценки. Большой раздел современной математической статистики — статистический последовательный анализ, фундаментальный вклад в создание и развитие которого внёс А. Вальд во время Второй мировой войны. В отличие от традиционных (непоследовательных) методов статистического анализа, основанных на случайной выборке фиксированного объема, в последовательном анализе допускается формирование массива наблюдений по одному (или, более общим образом, группами), при этом решение о проведении следующего наблюдения (группы наблюдений) принимается на основе уже накопленного массива наблюдений. Ввиду этого, теория последовательного статистического анализа тесно связана с теорией оптимальной остановки. В математической статистике есть общая теория проверки гипотез и большое число методов, посвящённых проверке конкретных гипотез. Рассматривают гипотезы о значениях параметров и характеристик, о проверке однородности (то есть о совпадении характеристик или функций распределения в двух выборках), о согласии эмпирической функции распределения с заданной функцией распределения или с параметрическим семейством таких функций, о симметрии распределения и др. Большое значение имеет раздел математической статистики, связанный с проведением выборочных обследований, со свойствами различных схем организации выборок и построением адекватных методов оценивания и проверки гипотез. Задачи восстановления зависимостей активно изучаются более 200 лет, с момента разработки К. Гауссом в 1794 г. метода наименьших квадратов. Разработка методов аппроксимации данных и сокращения размерности описания была начата более 100 лет назад, когда Карл Пирсон создал метод главных компонент. Позднее были разработаны факторный анализ и многочисленные нелинейные обобщения. Различные методы построения (кластер-анализ), анализа и использования (дискриминантный анализ) классификаций (типологий) именуют также методами распознавания образов (с учителем и без), автоматической классификации и др. В настоящее время компьютеры играют большую роль в математической статистике. Они используются как для расчётов, так и для имитационного моделирования (в частности, в методах размножения выборок и при изучении пригодности асимптотических результатов). Постановка задачиТребуется определить среднюю арифметическую интервального вариационного ряда; медиану; моду; медиану и моду графически по известной кумуляте и гистограмме ряда распределения; размах вариации; среднее линейное отклонение; дисперсию; среднее квадратическое отклонение; квартильное отклонение; первую, вторую и третью квартили; относительные показатели вариации (коэффициент осцилляции, относительное линейное отклонение, коэффициент вариации, относительный показатель квартильной вариации); показатель фондовой и децильной дифференциации. Условие: в качестве условия используется сгруппированный вариационный ряд: 0,72;0,76;0,86;0,88;0,88;0,91;0,94;0,96;0,98;1,01;1,03;1,11;1,13;1,28;1,38;1,38;1,38;1,43;1,43;1,44;1,47;1,49;1,49;1,49;1,51;1,53;1,53;1,53;1,53;1,53;1,56;1,56;1,57;1,57;1,57;1,58;1,59;1,61;1,61;1,61;1,61;1,62;1,63;1,63;1,65;1,68;1,69;1,73;1,86;1,86;1,9;1,9;1,9;1,91;1,94;2,01. В таблице 1 отображены номера промежутков, рентабельность активов и количество банков (частота). Таблица 1
Выполнение заданияИзучение средних величин первичной статистической информации имеет важное значение для анализа изучаемого признака в исследуемой совокупности разрозненных данных. Средняя величина является обобщающей характеристикой представленного ряда величин, отражает его типичный уровень в конкретных условиях определенного времени и места. Средняя арифметическая Рассчитать среднюю арифметическую дискретного ряда можно по формуле: 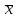 = =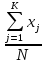 . .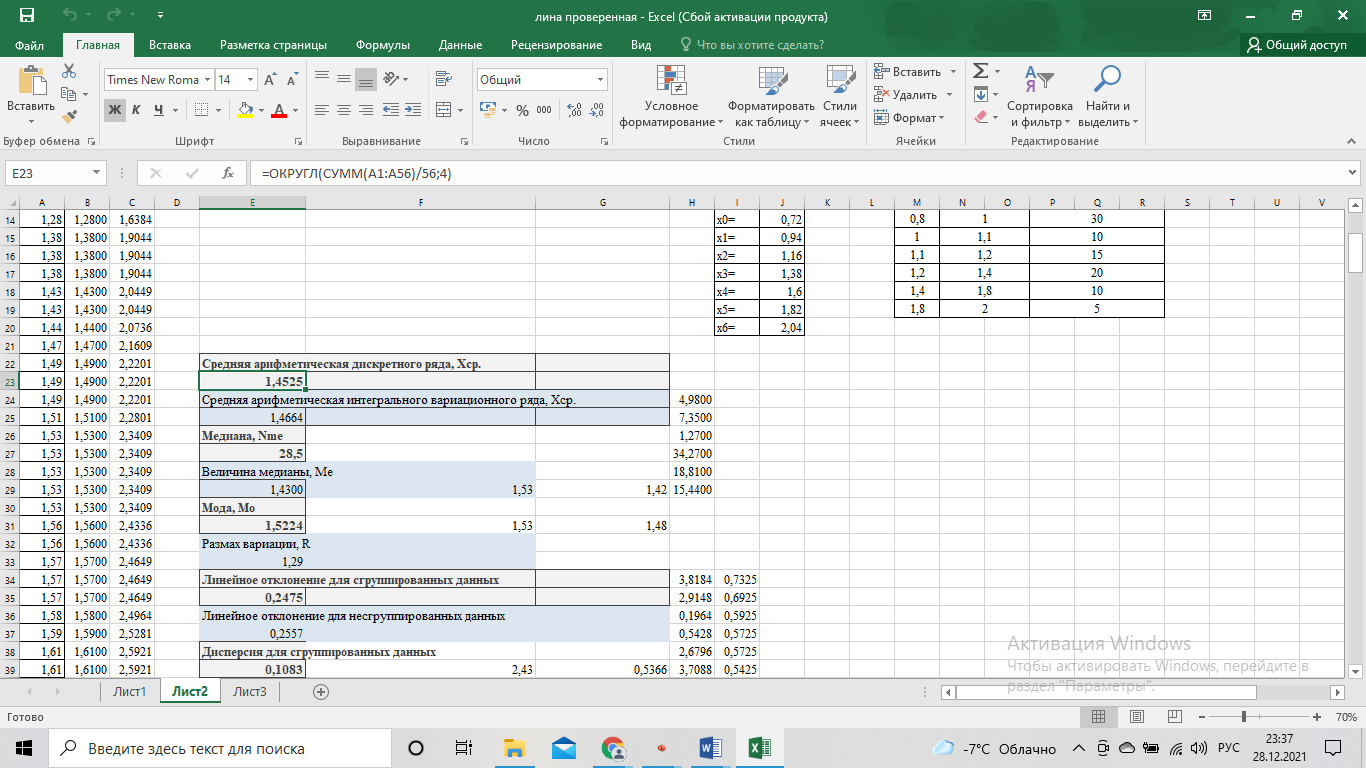 В интервальном вариационном ряду средняя арифметическая определяется по другой формуле: 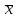 = =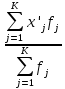 , где , где 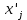 – середина соответствующего интервала варианта значений признака; – середина соответствующего интервала варианта значений признака;  – частота повторений данного варианта; j – номер варианты. – частота повторений данного варианта; j – номер варианты.В таблице 2 приведены значения середин соответствующих интервалов ряда вариант. Таблица 2
В интервальном ряду  = = 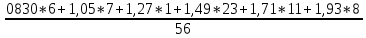 = 1,4664. = 1,4664. МедианаВысчитывается медиана. Она соответствует варианте, стоящей в середине ранжированного ряда. Ее положение в ряду определяется номером:  , где N – число единиц совокупности. Значит , где N – число единиц совокупности. Значит  . Для определения величины медианы интервального вариационного ряда используется формула Me= . Для определения величины медианы интервального вариационного ряда используется формула Me=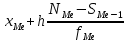 , где , где  - нижняя граница медианного интервала; h – величина интервала; - нижняя граница медианного интервала; h – величина интервала;  - накопленная частота интервала, предшествующего медианному; - накопленная частота интервала, предшествующего медианному; 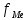 – частота медианного интервала. – частота медианного интервала. По накопленной частоте 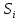 определяем, что медиана находится в интервале 1,16 - 1,38 и вспомогательные параметры соответственно равны: определяем, что медиана находится в интервале 1,16 - 1,38 и вспомогательные параметры соответственно равны:  = 1,16; h = 0,22; = 1,16; h = 0,22;  = 37; = 37; 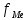 = 11. Тогда, Ме=1,16+0,22 = 11. Тогда, Ме=1,16+0,22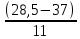 =1,43. =1,43.Полученное значение медианы не совпадает со значением, полученным на графике. Медиана представлена графически на рисунке 1 как абсцисса середины промежутка ординат накопленных частот в пределах от 0 до 56 кумуляты ряда распределения. Практически это означает, что 50% банков с доходами от 50 до 100 млн р имеют рентабельность активов менее 1,3, остальные – более 1,3. 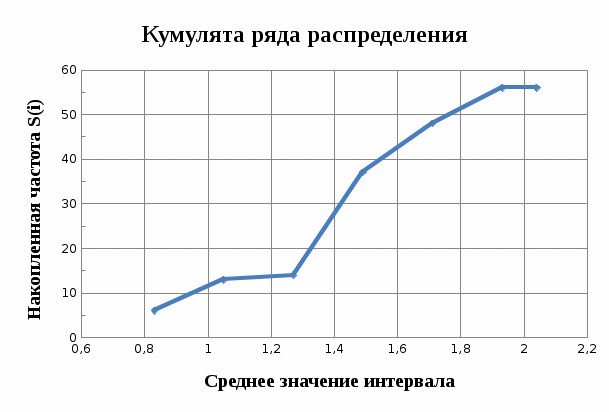 Рисунок 1 – Значение медианы Me гр =1,43 Mерасч = 1,53 Меexcel = 1,42 МодаОпределяется значение моды. Мода – наиболее часто встречающееся значение признака совокупности. Наибольшая частота f3 соответствует интервалу 1,38 - 1,6. Ее величину определяют по формуле Мо=xMo+h 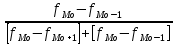 , где xMo – нижняя граница модального интервала; , где xMo – нижняя граница модального интервала; 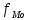 – частота, соответствующая модальному интервалу; – частота, соответствующая модальному интервалу; 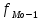 – предмодальная частота; – предмодальная частота;  – послемодальная частота. – послемодальная частота. Для приведенного вариационного ряда с равными интервалами для определения Мо используется формула, тогда Мо=1,38+0,22  =1,5224. =1,5224.Мода, как и медиана, может быть определена графически. Графическое определение моды представлено на рисунке 2. Таким образом, в данной совокупности наиболее часто встречается рентабельность активов, равная 1,5224 для банков с доходами от 50 до 100 млн р. 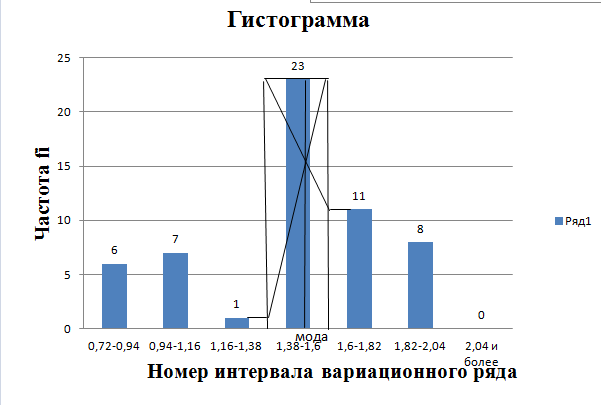 Рисунок 2 – Графическое определение моды По рисунку 2 можно сделать вывод, что мода входит в интервал и совпадает с полученной в результате расчетов модой, равной 1, 5224. Moгр= 1,5224 Морасч=1,53 Моexcel=1,48 Размах вариации Размах вариации – разность между максимальным и минимальным значениями признака совокупности. R = 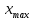 - - 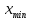 ; R = 2,01 – 0,72 = 1,29. ; R = 2,01 – 0,72 = 1,29.Среднее линейное отклонение Рассчитать среднее линейное отклонение  по формулам для сгруппированных данных по формулам для сгруппированных данных 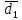 = = , где К – число групп совокупности, наибольшее значение варианты и для несгруппированных данных , где К – число групп совокупности, наибольшее значение варианты и для несгруппированных данных 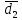 = = , где , где  = 1, 4525. = 1, 4525.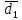 = 0,2475 = 0,2475 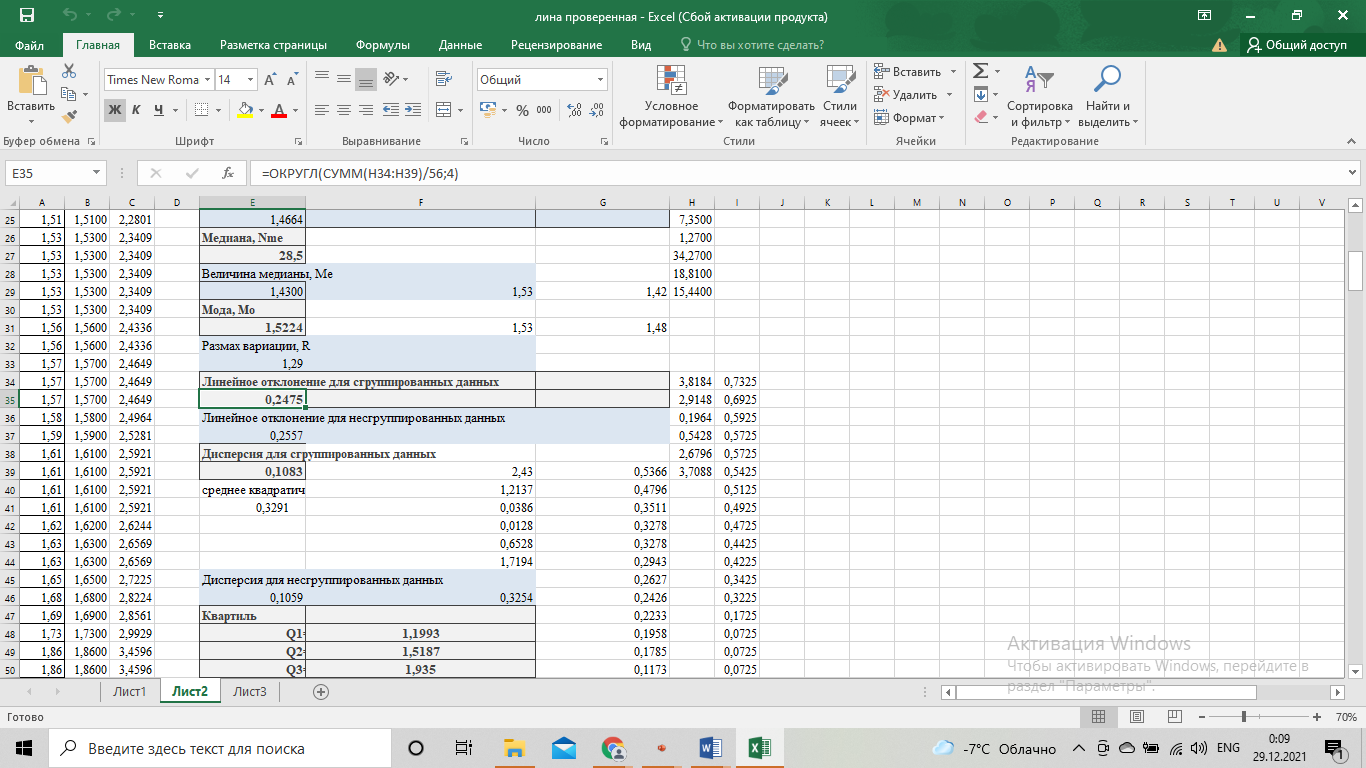 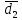 = 0,2557 = 0,2557 Применяя формулы для сгруппированных и не сгруппированных данных в среде Excel (рисунки 3, 4) получим 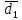 = 0,2475, = 0,2475, 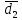 = 0,2557. = 0,2557.  Рисунок 3 – Нахождение 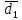    Рисунок 4 – Нахождение 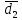 Дисперсия и среднеквадратическое отклонение дискретного рядаНахождение дисперсии и среднеквадратического отклонения дискретного ряда. Дисперсия – средняя из квадратов отклонений вариантов значений признака от их средней величины. Среднее квадратичное отклонение представляет собой корень квадратный их дисперсии. Различают дисперсию для сгруппированных данных: σ2 =  , где К – число групп совокупности, наибольшее значение варианты. Для не сгруппированных данных σ2 = , где К – число групп совокупности, наибольшее значение варианты. Для не сгруппированных данных σ2 =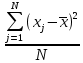 . .σ2 = 0,1083 – для сгруппированных; σ2 = 0,1059 – для не сгруппированных. Применяя формулы для сгруппированных и не сгруппированных данных в среде Excel получим: σ2=0, 1083, σ2=0, 1059. Среднее квадратическое отклонение σ=0,3291. Нахождение дисперсии для сгруппированного и не сгруппированного ряда, а также нахождение среднеквадратического отклонения представлены на рисунках 5,6. Дисперсия для сгруппированных данных    Рисунок 5 – Нахождение дисперсии сгруппированных данных Дисперсия для несгруппированных данных     Рисунок 6 – Нахождение дисперсии несгруппированных данных 2.7 Нахождение квартилейКвартили – значения признака в ранжированном ряду распределения, выбранные специальным образом. Четверть единиц должна быть меньше по величине, чем Q1; другая четверть единиц заключена между значениями Q1 и Q2; третья четверть единиц – между значениями Q2 и Q3; остальные – превосходят Q3. Значения Qi (i= 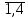 ) вычисляются по формулам, аналогичным формуле для расчета медианы: Q1= ) вычисляются по формулам, аналогичным формуле для расчета медианы: Q1=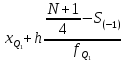 , где , где  - нижняя граница интервала, в котором находится первая квартиль; - нижняя граница интервала, в котором находится первая квартиль; 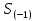 - сумма накопленных частот интервалов, предшествующих интервалу, в котором находится первая квартиль; - сумма накопленных частот интервалов, предшествующих интервалу, в котором находится первая квартиль; 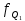 - частота интервала, в котором находится первая квартиль. Таким же образом определяются Q2 и Q3. - частота интервала, в котором находится первая квартиль. Таким же образом определяются Q2 и Q3.Вычислим первую, вторую и третью квартили по формулам: Q1=  = 1,1993; = 1,1993;  Q2= 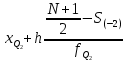 = 1,5187. = 1,5187. Q3=  =1,935. =1,935.  Сравним вычисленные величины квартилей с величинами, полученными применением статистических функций «Квартиль» порядка 1, 2 и 3 к дискретному ранжированному ряду в программной среде Excel (рисунок 6). Квартильное отклонение Q можно использовать для обобщения характеристики вариаций признаков в рассматриваемой совокупности, если по каким – либо причинам невозможно определение крайних значений рядов распределения с открытыми границами, то Q= 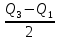 =0,3679. Для симметричных или мало симметричных распределений Q≈ =0,3679. Для симметричных или мало симметричных распределений Q≈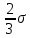 =0,2194 =0,2194 Рисунок 7 – Квартили 2.8 Относительные показатели вариацииОтносительные показатели вариации используются для сравнения колеблемости различных признаков в одной и той же совокупности или при сравнении колеблемости одного и того же признака в нескольких совокупностях. Коэффициент осцилляции КR=  100%, относительное линейное отклонение 100%, относительное линейное отклонение 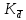 = = 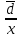 *100%, коэффициент вариации v= *100%, коэффициент вариации v=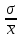 *100%, относительный показатель квартильной вариации *100%, относительный показатель квартильной вариации  *100%; *100%; = 1,29/1,45*100=88,97% = 1,29/1,45*100=88,97%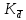 = 16,8781% = 16,8781%v=22,4427%  =25,7238% =25,7238%Совокупность является однородной, если коэффициент вариации не превышает 33%. Поскольку v = 22,4427% < 33%, то по размеру рентабельности и прибыли совокупность банков является однородной. 3.9 Показатель фондовой дифференциацииНайти показатель фондовой дифференциации. Он рассчитывается по первичным данным и характеризует отношение средней величины из 10% наибольших значений совокупности к средней величине из 10% наименьших значений совокупности: КФ = 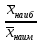 . . Пять коммерческих банков, что составляет 10% от общего количества банков, имеют наибольший уровень рентабельности, поэтому 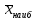 = =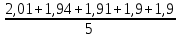 =1,9320. И пять коммерческих банков имеют наименьший уровень рентабельности, поэтому =1,9320. И пять коммерческих банков имеют наименьший уровень рентабельности, поэтому 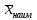 = = =0,8200. Следовательно, коэффициент фондовой дифференциации будет таким: КФ=2,3561. =0,8200. Следовательно, коэффициент фондовой дифференциации будет таким: КФ=2,3561.Это означает, что размер рентабельности у 10 % банков с наивысшими доходами в 2,3561 раза превышает размер прибыли 10% коммерческих банков с наименьшими доходами. Для определения децильной дифференциации используются формулы расчета квартилей. Сначала находится номер первой децили  = = , затем девятой - , затем девятой - 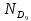 = =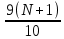 . .  =5,7; =5,7; 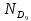 =51,3. =51,3.D1=0,929 D9=1,9108 Коэффициент децильной дифференциации устанавливается из соотношения: KD= 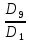 =2,056 =2,056Это означает, что отношение децили наиболее рентабельных банков в совокупности к децили наименее рентабельных банков составляет 2,056. Таким образом, уровень рентабельности наиболее прибыльных банков в 2,056 раз выше уровня наименее прибыльных банков. 3 ВыводВ ходе лабораторной работы были приобретены навыки обработки и обобщения индивидуальных значений одного и того же признака у различных единиц совокупности. Рассчитали средние арифметические в дискретном и интервальном рядах, они равны 1,4525 и 1,4664 соответственно; Рассчитали значение медианы, Ме=1,43. Оно не совпало со значением, найденным графически. Практически это означает, что 50% банков с доходами от 50 до 100 млн р имеют рентабельность активов менее 1,43, остальные – более 1,43; Рассчитали значение моды, Мо=1,5224. Таким образом, в данной совокупности наиболее часто встречается рентабельность активов, равная 1,5224для банков с доходами от 50 до 100 млн р.; Средние показатели (мода, медиана, средняя арифметического дискретного ряда) неравны, а это значит, что ряды несимметричны. Выяснили, что для ассиметричных рядов распределения медиана находится между средней арифметической и модой. Рассчитали размах вариации, он равен 1,29; Рассчитали значение среднего линейного отклонения. Для сгруппированных данных оно равно 0,2475, для не сгруппированных 0,2557; Рассчитали значение дисперсии сгруппированных данных, она равна 0,1083; дисперсия для не сгруппированных данных равна 0,1059; среднее квадратическое отклонение дискретного ряда равно 0,3291; Рассчитали значения квартилей, они равны 1,1993; 1,5187; 1,935. Значение второй квартили совпало с медианой. Рассчитали относительные показатели вариации. Коэффициент осцилляции равен 22,4427%; относительное линейное отклонение 16,8781%; коэффициент вариации 22,7238%; относительный показатель квартильной вариации 25,7238%. Совокупность является однородной, если коэффициент вариации не превышает 33%. Поскольку v=22,7238% < 33%, то по размеру рентабельности и прибыли совокупность банков является однородной; Рассчитали показатель фондовой дифференциации, он равен 2,3561. Это означает, что размер рентабельности у 10 % банков с наивысшими доходами в 2,3561 раза превышает размер прибыли 10% коммерческих банков с наименьшими доходами. Также определили коэффициент децильной дифференциации, он равен 2,056. Это означает, что отношение децили наиболее рентабельных банков в совокупности к децили наименее рентабельных банков составляет 2,056. Таким образом, уровень рентабельности наиболее прибыльных банков в 2,056 раз выше уровня наименее прибыльных банков. Список использованных источников 1. Гмурман В.Е. Теория вероятностей и математическая статистика. М.: Высш. шк., 1977. 2. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. М.: Высш. шк., 1997. 3. Мацкевич И.П., Свирид Г.П., Булдык Г.М. Сборник задач и упражнений по высшей математике (Теория вероятностей и математическая статистика). Минск: Вышейш. шк., 1996. 4. Тимофеева Л.К., Суханова Е.И., Сафиулин Г.Г. Сборник задач по теории вероятностей и математической статистике / Самарск. экон. ин-т. Самара, 1992. 5. Тимофеева Л.К., Суханова Е.И., Сафиулин Г.Г. Теория вероятностей и математическая статистика / Самарск. гос. экон. акад. Самара, 1994. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
