Лабораторная работа 2 Свободные колебания в последовательном rlc контуре
 Скачать 118 Kb.
|
|
Лабораторная работа № 6.2 Свободные колебания в последовательном RLC- контуре Цель работы: наблюдение затухающих колебаний на экране осциллографа и экспериментальное определение характеристик колебаний и параметров контура. Работа выполняется на ЭВМ. Краткая теория П 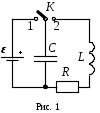 оследовательный RLC-контур - простейшая электрическая цепь, состоящая из последовательно соединенных конденсатора емкости С, катушки индуктивности L и омического сопротивления R (см. рис. 1). Величины R, LиCявляются параметрами контура.Чтобы в контуре возникли электромагнитные колебания, его необходимо вывести из состояния равновесия. Для этого ключ К следует перевести в положение 1, при этом конденсатор зарядится до напряжения, равного значению ЭДС ε. После переключения ключа в положение 2 начнется процесс разрядки конденсатора через резистор R и катушку L. Это приведет к появлению в катушке индуктивности нарастающего тока и пропорционального ему магнитного поля. ЭДС самоиндукции, возникающая при этом, сначала препятствует разрядке конденсатора, затем перезаряжает его. После перезарядки конденсатора процесс повторяется с той лишь разницей, что ток будет протекать в противоположном направлении. Реальный колебательный контур всегда обладает омическим сопротивлением R, поэтому в таком контуре электромагнитная энергия, запасенная в начале колебаний, постепенно превращается в тепловую в соответствии с законом Джоуля - Ленца. В результате амплитуда колебаний с течением времени уменьшается, - колебания затухают. Эти колебания называются свободными, т.к. они совершаются за счет первоначально сообщенной контуру энергии при последующем отсутствии внешних воздействий на колебательную систему. Дифференциальное уравнение затухающих электромагнитных колебаний имеет вид:  , (1)где Uc- напряжение на конденсаторе, β – коэффициент затухания, 0 - частота собственных колебаний контура. Эти величины связаны с параметрами контура:  (2) (3)Решение уравнения (1) при малом затухании (при условии 0 >> ) имеет вид:  , (4)где Uc0 - максимальное напряжение на конденсаторе, ω - частота затухающих колебаний. Частота затухающих колебаний зависит от параметров контура:  . (5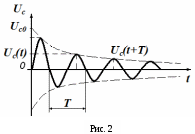)А  мплитуда колебаний убывает по закону: . (6)График затухающих колебаний, соответствующий уравнению (4), представлен на рис. 2. Для количественной характеристики быстроты затухания вводят логарифмический декремент затухания λ - натуральный логарифм отношения двух последовательных амплитуд колебаний:  . (7)Период затухающих колебаний: 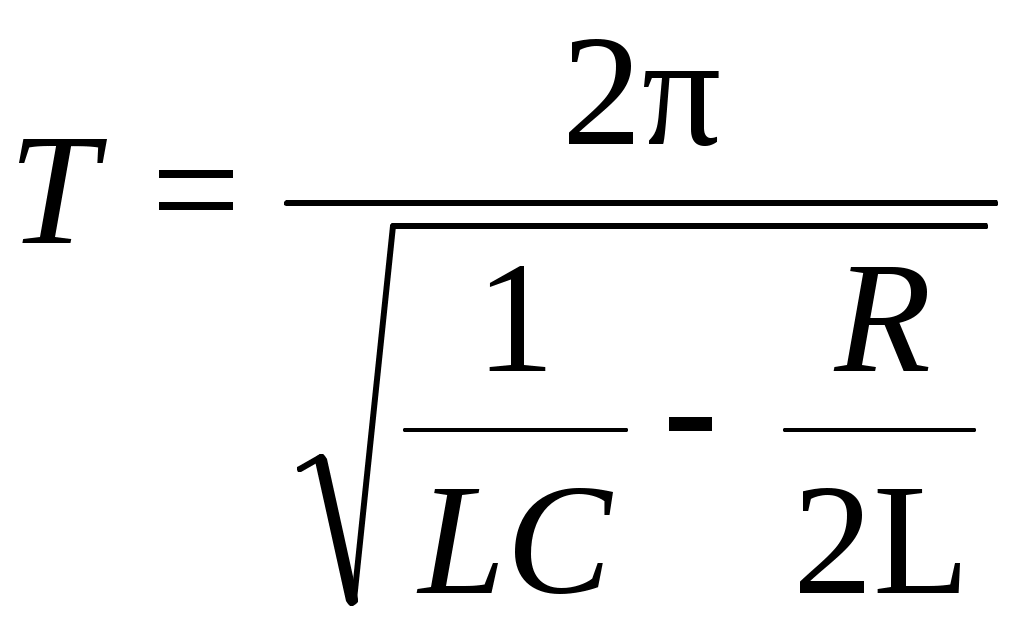 (8)Затухание колебаний в контуре характеризуют также добротностью контура Q, которая определяет относительные потери энергии за один период колебаний:  . (9)При малом затухании:  . (10)Величина β также характеризует скорость убывания амплитуды колебаний. Это величина. обратная времени, за которое амплитуда колебаний уменьшится в e раз. При β = 0 (при R = 0) амплитуда с течением времени изменяться не будет, колебания при этом будут собственными. Они происходят с частотой, определяемой формулой (3). С увеличением сопротивления контура коэффициент затухания растет, частота уменьшается, а период затухающих колебаний увеличивается. При 0 колебания в системе невозможны. При выведении ее из положения равновесия происходит апериодический процесс возврата системы в исходное состояние: напряжение на конденсаторе уменьшается по экспоненциальному закону, асимптотически приближаясь к нулю. Сопротивление контура, при котором колебательный процесс переходит в апериодический, называется критическим Rкрит.. Величину критического сопротивления определяют из условия 2 = 02:  . (11)Порядок выполнения работы Откройте диалоговое окно (щёлкнув дважды по «R.L.C-контур. Свободные колебания» на рабочем столе). В 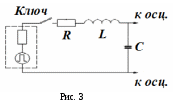 работе моделируется процесс свободных затухающих колебаний в схеме, изображенной на рис. 3. Генератор формирует импульсы напряжения прямоугольной формы, которые периодически заряжают конденсатор С контура. При последующем разряде конденсатора в контуре возникают свободные затухающие колебания, регистрируемые с помощью осциллографа: на его экране можно получить картину затухающих колебаний, показанную на рис. 2, активируя «мышкой» кнопку «КЛЮЧ». Длительность импульсов генератора много меньше периода Тг их повторения, поэтому в интервале (Тг – ) колебания в контуре успевают затухать. Выберите катушку индуктивности согласно варианту выполнения лабораторной работы, заданному в «Руководстве по выполнению лабораторных работ» (l1. l2 или l3). Установите R = 0. Получите на экране осциллографа картину свободных затухающих колебаний в контуре (активируя «мышкой» кнопку «КЛЮЧ») при любом значении электроемкости конденсатора С (значение С занесите в таблицу). Таблица
Для контура с установленным значением электроемкости по картине затухающих колебаний измерьте и запишите в таблицу две последовательные амплитуды напряжения на конденсаторе. По этим данным рассчитайте λ по формуле (7). Изменяя цену деления по осям X и Y (активируя кнопки «+» и «-»), установите одно полное колебание во весь экран осциллографа. Измерьте и запишите в табл. 1 период колебаний (обратите внимание единицы измерения величин на экране осциллографа). Повторите действия пункта 6 для остальных значений ёмкости С при нулевом сопротивлении R. Используя формулу (8) с учетом R = 0 рассчитайте и запишите в табл. 1 величину индуктивности контура для каждого значения электроемкости. Определите среднее значение индуктивности контура и найдите абсолютную и относительную погрешности этой величины по правилам обработки результатов косвенных невоспроизводимых измерений. Изменяя значения сопротивления при постоянных индуктивности и емкости пронаблюдайте изменения на экране осциллографа картины свободных затухающих колебаний в контуре. Сделайте выводы. Контрольные вопросы. Свободные колебания в контуре RLC-контуре, условия их возникновения, дифференциальное уравнение этих колебаний и его решение. Частота свободных колебаний в реальном контуре. Закон убывания амплитуды колебаний. Отличия свободных колебаний в реальном и идеальном контуре. Апериодический разряд конденсатора, условия его возникновения. Методика определения индуктивности контура в данной работе. |