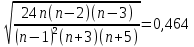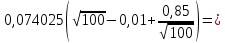 0,746 0,746
Так как Dnн=0,746 < DnН(0,05) = 0,895, гипотеза о нормальном распределении не отклоняется.
Критерий Колмогорова для сгруппированной выборки:
xi
|
ni
|
ni'
|
wi
|
wi'
|
|wi-wi'|
|
71
|
1
|
2
|
1
|
2
|
1
|
73,6
|
8
|
5
|
9
|
7
|
2
|
76,2
|
13
|
9
|
22
|
16
|
6
|
78,8
|
11
|
13
|
33
|
29
|
4
|
81,4
|
10
|
16
|
43
|
45
|
2
|
84
|
23
|
17
|
66
|
62
|
4
|
86,6
|
6
|
15
|
72
|
77
|
5
|
89,2
|
12
|
11
|
84
|
88
|
4
|
91,8
|
11
|
7
|
95
|
95
|
0
|
94,4
|
3
|
4
|
98
|
99
|
1
|
97
|
2
|
2
|
100
|
101
|
1
|
λ = 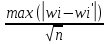 = = 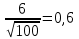
4) Критерий Ямстремского
а) без объединения интервалов
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xi
|
ni
|
ni'
|
pi'
|
qi'
|
(ni-ni')2
|
ni'qi'
|
(ni-ni')2/(ni'qi')
|
71
|
1
|
2
|
0,02
|
0,98
|
1
|
1,96
|
0,510204082
|
73,6
|
8
|
5
|
0,05
|
0,95
|
9
|
4,75
|
1,894736842
|
76,2
|
13
|
9
|
0,09
|
0,91
|
16
|
8,19
|
1,953601954
|
78,8
|
11
|
13
|
0,13
|
0,87
|
4
|
11,31
|
0,353669319
|
81,4
|
10
|
16
|
0,16
|
0,84
|
36
|
13,44
|
2,678571429
|
84
|
23
|
17
|
0,17
|
0,83
|
36
|
14,11
|
2,551381999
|
86,6
|
6
|
15
|
0,15
|
0,85
|
81
|
12,75
|
6,352941176
|
89,2
|
12
|
11
|
0,11
|
0,89
|
1
|
9,79
|
0,102145046
|
91,8
|
11
|
7
|
0,07
|
0,93
|
16
|
6,51
|
2,457757296
|
94,4
|
3
|
4
|
0,04
|
0,96
|
1
|
3,84
|
0,260416667
|
97
|
2
|
2
|
0,02
|
0,98
|
0
|
1,96
|
0
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c = 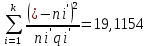
J = |c-k | = |19,1154 - 11| = 8,1154
J< 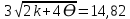
Условие принятия гипотезы выполняется.
б) для случая объединения интервалов
Эмпирические частоты ni
|
pi
|
Теоретические частоты npi
|
(ni-npi)^2/npi(1-pi)
|
число интервалов k
|
сумма (ni-npi)^2/npi(1-pi)
|
|сумма (ni-npi)^2/npi(1-pi)-k|/√2k-4θ
|
9
|
0,086417
|
8,64167
|
0,016263673
|
6
|
52,25387281
|
14,92837326
|
13
|
0,171463
|
17,1463
|
1,210152259
|
|
|
|
11
|
0,286653
|
28,6653
|
15,26104003
|
|
|
|
10
|
0,35315
|
35,315
|
28,05383646
|
|
|
|
23
|
0,225975
|
22,5975
|
0,009261594
|
|
|
|
34
|
0,22424
|
22,424
|
7,703318788
|
|
|
|
Поскольку 14,93 > 3 , гипотеза не принимается.
5. Приближенный критерий
SAS = 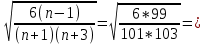 0,239 0,239
SEX = 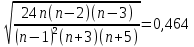
Условием принятия гипотезы о нормальном распределении являются условия (0,11149 < 0,239) и (-0,83256 < 0.464).Оба условия выполняются.
Вывод: гипотезу о соответствии данного распределения нормальному закону распределения принимаем. |
 Скачать 116.1 Kb.
Скачать 116.1 Kb.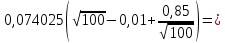 0,746
0,746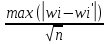 =
= 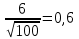
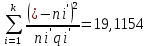
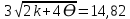
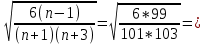 0,239
0,239