ЛАБОРАТОРНАЯ РАБОТА № 2
Вариант 17
Построение кривой нормального распределения по опытным данным. Проверка гипотезы о нормальном распределении выборки.
Содержание работы: на основе дискретного вариационного ряда, полученного в практической работе № 1, выполнить следующее:
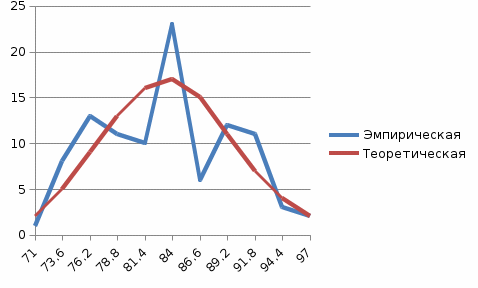
Построить эмпирическую (полигон) и теоретическую (нормальную) кривую распределения.
Проверить согласованность эмпирического распределения с теоретическим нормальным, применяя критерии:
а) Пирсона;
б) Колмогорова,
в) Романовского,
г) Ястремского;
д) приближенный критерий.
1. Построение эмпирической и теоретической кривых
Для построения теоретической кривой необходимо найти теоретические частоты ni’
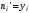 , где , где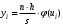 , , 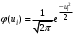 , ,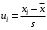
xi
|
ni
|
xi-xcp
|
ui
|
φ(ui)
|
yi
|
ni’
|
71
|
1
|
-12,402
|
-1,9885
|
0,055262341
|
2,303705084
|
2
|
73,6
|
8
|
-9,802
|
-1,5716
|
0,11606199
|
4,838242326
|
5
|
76,2
|
13
|
-7,202
|
-1,1547
|
0,204870699
|
8,540385094
|
9
|
78,8
|
11
|
-4,602
|
-0,7379
|
0,303947649
|
12,67057701
|
13
|
81,4
|
10
|
-2,002
|
-0,321
|
0,37900665
|
15,79953967
|
16
|
84
|
23
|
0,598
|
0,09588
|
0,397213474
|
16,55852226
|
17
|
86,6
|
6
|
3,198
|
0,51275
|
0,349888942
|
14,58571827
|
15
|
89,2
|
12
|
5,798
|
0,92961
|
0,259039243
|
10,79849338
|
11
|
91,8
|
11
|
8,398
|
1,34648
|
0,161186999
|
6,719355429
|
7
|
94,4
|
3
|
10,998
|
1,76335
|
0,084299221
|
3,514157027
|
4
|
97
|
2
|
13,598
|
2,18021
|
0,037054948
|
1,54469882
|
2
|
2. Проверка согласованности эмпирической функции с теоретическим нормальным распределением.
1) Критерий Пирсона
а) без объединения интервалов
Статистика критерия хи-квадрат:
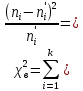 16,78 16,78
Для уровня значимости α=0,95 и числе степеней свободы l=k-r=11-3=8
p=1-α=0,05 и K=l=8 χкрит2 = 15,507
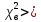 χкрит2, гипотезу о соответствии данного распределения нормальному закону не принимаем. χкрит2, гипотезу о соответствии данного распределения нормальному закону не принимаем.
б) Исходные данные
левая граница интервала
|
правая граница интервала
|
середина xi
|
ni
|
69,7
|
72,3
|
71
|
1
|
72,3
|
74,9
|
73,6
|
8
|
74,9
|
77,5
|
76,2
|
13
|
77,5
|
80,1
|
78,8
|
11
|
80,1
|
82,7
|
81,4
|
10
|
82,7
|
85,3
|
84
|
23
|
85,3
|
87,9
|
86,6
|
6
|
87,9
|
90,5
|
89,2
|
12
|
90,5
|
93,1
|
91,8
|
11
|
93,1
|
95,7
|
94,4
|
3
|
95,7
|
98,3
|
97
|
2
|
|
|
|
|
|
|
|
После объединения эмпир. Частот
|
Левая граница
|
Правая
|
pk
|
npk
|
(nk-npk)^2/npk
|
|
9
|
69,7
|
74,9
|
0,086417
|
8,641671
|
0,014858
|
|
13
|
74,9
|
77,5
|
0,171463
|
17,1463
|
1,002656
|
|
11
|
77,5
|
80,1
|
0,286653
|
28,66529
|
10,88642
|
|
10
|
80,1
|
82,7
|
0,35315
|
35,31497
|
18,14663
|
|
23
|
82,7
|
85,3
|
0,225975
|
22,59751
|
0,007169
|
|
34
|
85,3
|
98,3
|
0,22424
|
22,42399
|
5,975928
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
χв^2
|
36,03366
|
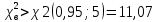
Гипотезу о нормальном распределении генеральной совокупности не принимаем.
2. Критерий Романовского
а) для случая без объединения интервалов:
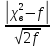 = = 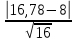 = 2,195 = 2,195
б) с объединением интервалов
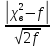 = = 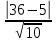 = 9,8 = 9,8
в обоих случаях не меньше 3, поэтому гипотезу не принимаем.
3) Критерий Колмогорова-Смирнова
|
|
|
|
|
|
|
|
xi
|
Эмпирические частоты
|
Накопленные частоты
|
F(xcp,s)
|
Fn(xi)
|
Fn(xi+1)
|
Dn-
|
Dn+
|
71
|
1
|
1
|
0,025526
|
0
|
0,01
|
0,025526
|
-0,01553
|
73
|
6
|
7
|
0,051016
|
0,01
|
0,07
|
0,041016
|
0,018984
|
74
|
2
|
9
|
0,069824
|
0,07
|
0,09
|
-0,00018
|
0,020176
|
75
|
2
|
11
|
0,093563
|
0,09
|
0,11
|
0,003563
|
0,016437
|
76
|
7
|
18
|
0,122791
|
0,11
|
0,18
|
0,012791
|
0,057209
|
77
|
4
|
22
|
0,15789
|
0,18
|
0,22
|
-0,02211
|
0,06211
|
78
|
4
|
26
|
0,199003
|
0,22
|
0,26
|
-0,021
|
0,060997
|
79
|
6
|
32
|
0,245975
|
0,26
|
0,32
|
-0,01402
|
0,074025
|
80
|
1
|
33
|
0,298323
|
0,32
|
0,33
|
-0,02168
|
0,031677
|
81
|
5
|
38
|
0,355225
|
0,33
|
0,38
|
0,025225
|
0,024775
|
82
|
5
|
43
|
0,415557
|
0,38
|
0,43
|
0,035557
|
0,014443
|
83
|
7
|
50
|
0,477953
|
0,43
|
0,5
|
0,047953
|
0,022047
|
84
|
10
|
60
|
0,540894
|
0,5
|
0,6
|
0,040894
|
0,059106
|
85
|
6
|
66
|
0,602825
|
0,6
|
0,66
|
0,002825
|
0,057175
|
86
|
2
|
68
|
0,662262
|
0,66
|
0,68
|
0,002262
|
0,017738
|
87
|
4
|
72
|
0,717903
|
0,68
|
0,72
|
0,037903
|
0,002097
|
88
|
6
|
78
|
0,76871
|
0,72
|
0,78
|
0,04871
|
0,01129
|
89
|
3
|
81
|
0,81396
|
0,78
|
0,81
|
0,03396
|
-0,00396
|
90
|
3
|
84
|
0,85327
|
0,81
|
0,84
|
0,04327
|
-0,01327
|
91
|
2
|
86
|
0,886581
|
0,84
|
0,86
|
0,046581
|
-0,02658
|
92
|
5
|
91
|
0,914112
|
0,86
|
0,91
|
0,054112
|
-0,00411
|
93
|
4
|
95
|
0,936308
|
0,91
|
0,95
|
0,026308
|
0,013692
|
94
|
1
|
96
|
0,953762
|
0,95
|
0,96
|
0,003762
|
0,006238
|
95
|
2
|
98
|
0,96715
|
0,96
|
0,98
|
0,00715
|
0,01285
|
96
|
1
|
99
|
0,977165
|
0,98
|
0,99
|
-0,00283
|
0,012835
|
97
|
1
|
100
|
0,984474
|
0,99
|
1
|
-0,00553
|
0,015526
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n
|
100
|
|
|
|
макс
|
0,054112
|
0,074025
|
|
|
|
|
|
|
|
|
Dn=max=0,074025
Dnн = |
 Скачать 116.1 Kb.
Скачать 116.1 Kb.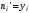 , где
, где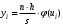 ,
, 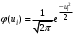 ,
,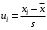

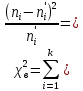 16,78
16,78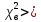 χкрит2, гипотезу о соответствии данного распределения нормальному закону не принимаем.
χкрит2, гипотезу о соответствии данного распределения нормальному закону не принимаем.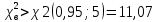
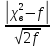 =
= 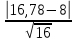 = 2,195
= 2,195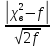 =
= 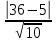 = 9,8
= 9,8