Статистика практика 1. Статистика. Практическое занятие 1. Практическое занятие 1 Графические представления анализа выборки. Построение гистограммы, полигона, кумуляты по интервальному вариационному ряду. Вычисление моды для дискретного и интервального вариационного ряда
 Скачать 16.95 Kb. Скачать 16.95 Kb.
|
|
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 1 Графические представления анализа выборки. Построение гистограммы, полигона, кумуляты по интервальному вариационному ряду. Вычисление моды для дискретного и интервального вариационного ряда. ПРИМЕР 1. (Построение гистограммы, полигона, кумуляты и эмпирической функции распределения) Найти эмпирическую функцию распределения значений механической скорости бурения, представленной в виде интервального вариационного ряда. Таблица 1.1 Исходный интервальный ряд
Примите количество интервалов К= . Постройте гистограмму, полигон и кумуляту. Решение Дополним имеющуюся таблицу сушенинами интервалов, относительными частотами согласно формуле 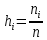 1) 1)и накопленными относительными частотами, согласно формуле Wi Wi-1 hi (1.2) Таблица 1.2 Интервальный ряд, дополненный необходимыми параметрами для построения графиков
Построим гистограмму и полигон частот (относительных частот). На рис.1.1. Изображена гистограмма и полигон относительных частот. График был построен при помощи электронных таблиц Microsoft Office. Рис.1.1 Гистограмма и полигон частот Используя накопленные относительные частоты (таб. 1.2) построим эмпирическую функцию распределения. Заметим, что при этом следует пользовать не интервальным представлением 5 вариационного ряда, а его представлением через середины интервалов. Таким образом, в аналитическом виде F (x) n записывается следующим образом: Построим кумуляту и эмпирическую функцию распределения. Для интервальных данных ломаная линия начинается с точки, абсцисса которой равна началу первого интервала, а ордината – накопленной частоте, равной нулю. Другие точки этой ломаной соответствуют концам интервалов и накопленным частотам. Эмпирическая функция распределения строится согласно её аналитической записи и имеет скачки в серединах интервалов. Диаграмма значений функции распределения и кумулята представлены на рис.2.2. Рис.2.2. Кумулята и диаграмма эмпирической функции распределения. ПРИМЕР 2. (Вычисление моды для дискретного и интервального вариационного ряда) Таблица 2.1. Исходный дискретный вариационный ряд
Очевидно, что модой в этом случае является 61,2, так как имеет наибольшую частоту. Пусть выборка представлена в виде интервального вариационного ряда Таблица 2.2. Таблица 2.2. Интервальный вариационный ряд
Определим моду по интервальному вариационному ряду. Для этого определим интервал, которому соответствует наибольшая частота. Третьему интервалу (9;11) соответствует наибольшая частота 11 n3 . Тогда вычисляется мода: 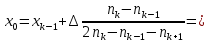 |
