Документ Microsoft Word. Контрольная работа по дисциплине Статистика
 Скачать 27.93 Kb. Скачать 27.93 Kb.
|
|
Контрольная работа по дисциплине: «Статистика» Вариант 19 Выполнил: Проверил: 2021 Решение: Для расчетов заменим интервалы их средними значениями. Величины первого и последнего открытых интервалов условно примем равными величинам второго и предпоследнего интервалов соответственно. Заполним вспомогательную расчетную таблицу: Таблица 1
Мода. Мода - наиболее часто встречающееся значение признака у единиц данной совокупности. 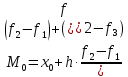 , где , гдеx0 – начало модального интервала; h – величина интервала; f2 –частота, соответствующая модальному интервалу; f1 – предмодальная частота; f3 – послемодальная частота. Выбираем в качестве начала интервала 800, так как именно на этот интервал приходится наибольшее количество. 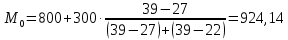 Вывод: наиболее часто встречающееся значение ряда – 924,14 Медиана. Медиана делит выборку на две части: половина вариант меньше медианы, половина — больше. Медианным является интервал 800 - 1100, т.к. в этом интервале накопленная частота S, больше медианного номера (медианным называется первый интервал, накопленная частота S которого превышает половину общей суммы частот). Me = 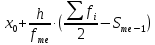 Me = 800 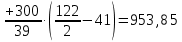 Вывод: таким образом, 50% единиц совокупности будут меньше по величине 953,846, другие 50% будут больше величины 953,85. Квартили. Квартили – это значения признака в ранжированном ряду распределения, выбранные таким образом, что 25% единиц совокупности будут меньше по величине Q1, 25% будут заключены между Q1 и Q2, 25% - между Q2 и Q3. Остальные 25% превосходят Q3. 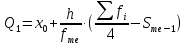 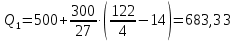 Вывод: таким образом, 25% единиц совокупности будут меньше по величине 683,33. Q2 совпадает с медианой, Q2 = 953,846 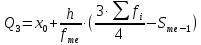 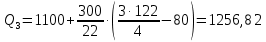 Вывод: Остальные 25% превосходят значение 1256,82. Квартильный коэффициент дифференциации. k = Q1 / Q3 k = 683,33 / 1256,82 = 0,54 Децили. Децили делят ряд распределения признака по частоте на 10 равных частей. Рассчитаем второй, четвертый и седьмой децили. 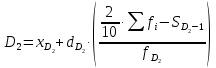 , где , где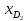 – начальные значения второго децильного интервала; – начальные значения второго децильного интервала; i – величина децильного интервала; Σf – сумма частот ряда; 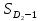 – накопленные частоты интервала, предшествующего децильному; – накопленные частоты интервала, предшествующего децильному;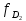 – частота децильного интервала. – частота децильного интервала.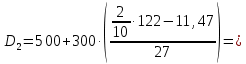 643,67 643,67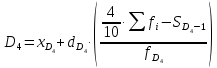 , где , где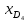 – начальные значения четвертого децильного интервала; – начальные значения четвертого децильного интервала; i – величина децильного интервала; Σf – сумма частот ряда; 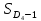 – накопленные частоты интервала, предшествующего децильному; – накопленные частоты интервала, предшествующего децильному;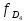 – частота децильного интервала. – частота децильного интервала.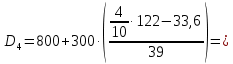 916,92 916,92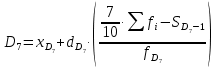 , где , где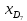 – начальные значения четвертого децильного интервала; – начальные значения четвертого децильного интервала; i – величина децильного интервала; Σf – сумма частот ряда; 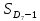 – накопленные частоты интервала, предшествующего децильному; – накопленные частоты интервала, предшествующего децильному;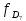 – частота децильного интервала. – частота децильного интервала.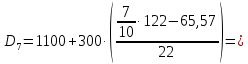 1 370,41 1 370,41СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ Ниворожкина, Л.И. Статистика: учебник для бакалавров: учебник /. - Москва: Дашков и К: Наука-Спектр, 2019. - 415 с. Практикум по теории статистики: учеб. пособие /под ред. проф. Р. А. Шмойловой. – М.: Финансы и статистика, 2019. Статистика: учебник/ [Елисеева и др.]. - Москва: Проспект, 2017. -443 с. Статистика: учебно-практическое пособие / [Назаров и др.]. - Москва: КноРус, 2018. - 479 с. Теория статистики / под ред. проф. Р. А. Шмойловой. – М.: Финансы и статистика, 2018. |
