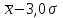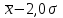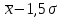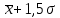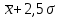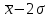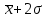Тема 4 Стат распределение и их осн характеристики. Тема 4 Статистические распределения и их основные характеристики 1 Ряды распределения и группировки. Принципы построения статистических группировок
 Скачать 233.87 Kb.
|
Тема 4: Статистические распределения и их основные характеристики4.1 Ряды распределения и группировки. Принципы построения статистических группировок.Различия индивидуальных значений признака у единиц совокупности называются вариацией признака. Она возникает в результате того, что индивидуальные значения складываются под совместным влиянием разнообразных условий (факторов), по-разному сочетающихся в каждом отдельном случае. Вариация наблюдается и в пределах однородной, выделенной по тому или другому группировочному признаку, группы. Вариация, которая не зависит от факторов, положенных в основу выделения групп, называется случайной вариацией. Изучение вариации в пределах однородной группы предполагает использование следующих приемов: построение вариационного ряда (ряда распределения), его графическое изображение, исчисление основных характеристик распределения. Вариационный ряд - групповая таблица, построенная по количественному признаку, в сказуемом которой показывается число единиц в каждой группе. Форма построения вариационного ряда зависит от характера изменения изучаемого признака, он может быть построен в форме дискретного ряда или в форме интервального ряда. По характеру вариации значений признака различают: признаки с прерывным изменением (дискретные); признаки с непрерывным изменением (непрерывные). Признаки с прерывным изменением могут принимать лишь конечное число определенных значений (например, тарифный разряд рабочих, число детей в семье, число станков, обслуживаемых одним рабочим). Признаки с непрерывным изменением могут принимать в определенных границах любые значения (например, стаж работы, пробег автомобиля, размер дохода и т. д.). Для признака, имеющего прерывное изменение и принимающего небольшое количество значений, применяется построение дискретного ряда. В первой графе ряда указываются конкретные значения каждого индивидуального значения признака, во второй графе - численность единиц с определенным значением признака. Для признака, имеющего непрерывное изменение, строится интервальный вариационный ряд, состоящий, так же как и дискретный ряд, из двух граф (варианты и частоты). При его построении в первой графе отдельные значения признака указываются в интервалах «от - до», во второй графе - число единиц, входящих в интервал. Интервалы образуются, как правило, равные и закрытые. Величина интервала определяется по формуле  где R - размах колебания (варьирования) признака;  ; m - число групп. Число групп приближенно определяется по формуле Стерджесса: m = 1 + 3,322 lg n, где n ‑ общее число единиц совокупности.
Полученную по этой формуле величину округляют до целого числа, поскольку количество групп не может быть дробным числом. При небольшом объеме информации (численности единиц в совокупности) число групп может быть установлено исследователем без использования формулы Стерджесса. Величину интервала обычно округляют до целого (всегда большего) числа, исключение составляют лишь случаи, когда изучаются малейшие колебания признака (например, при группировке деталей по величине размера отклонений от номинала, измеряемого в долях миллиметра). Нижнюю границу первого интервала принимают равной минимальному значению признака (чаще всего его предварительно округляют до целого числа); верхняя граница первого интервала соответствует значению  . Для последующих групп границы определяются аналогично, т.е. последовательно прибавляется величина интервала. Если единица обладает значением признака, равным величине верхней границы интервала, то ее следует относить к следующей группе.Другой способ определения числа групп основан на применении показателя среднего квадратического отклонения (σ). Если величина интервала равна 0,5σ, то совокупность разбивается на 12 групп, а когда величина интервала равна 2/3σ и σ, то совокупность делится соответственно на 9 и 6 групп. Если совокупность разбивается на 12 групп, то интервалы групп строятся следующим образом:
где  - среднее значение признака по совокупности, которое определяется по формуле:  ;σ - среднее квадратическое отклонение, которое определяется по формуле:  .Когда число групп равно 6, получаются следующие интервалы групп:
Эти методы не дают гарантии в том, что не будут сформированы «пустые» или малочисленные группы. «Пустыми» считаются группы, в которые не попала ни одна единица совокупности. Наличие таких интервалов свидетельствует, что группировка построена неправильно. Рассмотрим пример. Пусть требуется произвести группировку с равными интервалами предприятий по стоимости основных фондов, при этом максимальное значение признака равно 2040 млн. руб., а минимальное его значение - 290 млн. руб. Совокупность включает 80 единиц. Согласно формуле Стерджесса она должна быть разбита на 7 групп: m = 1 + 3,322 lg 80 = 1 + 3,322 · 1,90309 = 7,322065 ≈ 7 Сначала следует найти: R = 2040 - 290 = 1750 млн. руб. Затем определим величину интервала: i = 1750 : 7= 250 млн. руб. После этого построим интервалы групп (табл. 4.1). Таблица 4.1 - Варианты построения групп
Чтобы не писать каждый раз от ... до, границы групп обозначают следующим образом: 290 - 540, 540 - 790 и т. д. Особенностью первого варианта построения групп является то, что у всех групп имеются закрытые интервалы. Во втором варианте первая и последняя группы ‑ это группы с открытыми интервалами. Открытые ‑ это те интервалы, у которых указана только одна граница: верхняя - у первого, нижняя - у последнего. Закрытыми называются интервалы, у которых обозначены обе границы. Ширина открытого интервала принимается равной ширине смежного с ним интервала. При группировке по количественному признаку границы интервалов могут быть обозначены по-разному. Если основанием группировки служит непрерывный признак, то одно и то же значение признака выступает и верхней, и нижней границами у двух смежных интервалов. Таким образом, верхняя граница i-гo интервала равна нижней границе i + 1-го интервала. Примером такой группировки является приведенная ранее группировка предприятий по стоимости основных фондов. При таком обозначении границ может возникнуть вопрос, в какую группу включать единицы объекта, значения признака у которых совпадают с границами интервалов. Например, во вторую или третью группу должно войти предприятие со стоимостью фондов 790 млн. руб. (табл. 4.1). Если нижняя граница формируется по принципу «включительно», а верхняя - по принципу «исключительно», то предприятие должно быть отнесено к третьей группе, в противном случае - ко второй. При определении величины интервала и распределении единиц объекта наблюдения по группам важное значение имеет точное установление границ, которые в большинстве своем обозначаются указанием значений признака "от" и "до" для единиц, включаемых в данную группу. Например, группы товарных секций по числу работников обозначаются так: от 1 до 3 человек, 4-7,8-11,12-15 человек. Этот прием позволяет четко обозначить границы и правильно распределить единицы совокупности по группам. Однако в практике построения группировки нередко (при непрерывно изменяющемся признаке) одно и то же число служит верхней и нижней границами двух смежных групп. Например, группы работников магазина по производительности труда обозначаются так: до 90 тыс. руб., 90-120, 120-150, 150-180, свыше 180 тыс. руб. При таком построении интервалов вопрос об отнесении единиц объекта наблюдения по группам в практике решается двояко: по принципу "включительно" к первой группе относится работник, производительность труда которого обозначается - до 90 тыс. руб.; по принципу "исключительно" этот работник включается во вторую группу - 90-120 тыс. руб. Применение этих принципов зависит от формы написания интервалов, особенно первой и последней групп. В данном примере работника, производительность которого 180 тыс. руб., включают в предпоследнюю группу, поскольку ее интервал обозначен 150-180, а последний - свыше 180 тыс. руб. Соответственно работник, имеющий выработку 90 тыс. руб., относится к первой группе. Если бы запись была "180 и более", то по принципу "исключительно" работник, имеющий выработку 180 тыс. руб., включался бы в последнюю группу. В практике применяются оба метода, но все же предпочтительнее принцип "исключительно". Если в основании группировки лежит дискретный признак, то нижняя граница i-го интервала равна верхней границе i-1-го интервала, увеличенной на 1. Например, пусть совокупность состоит из 80 предприятий и ее надо разделить на группы по численности занятых. Минимальное и максимальное значения группировочного признака соответственно равны 290 и 2040 человек. В этом случае возможны следующие варианты построения групп (табл. 4.2). Таблица 4.2 – Варианты построения групп
Неравные интервалы применяются в статистике, когда значения признака варьируют неравномерно и в значительных размерах, что характерно для большинства социально-экономических явлений, особенно при анализе макроэкономических показателей. Неравные интервалы могут быть прогрессивно возрастающие или убывающие в арифметической или геометрической прогрессии. Величина интервалов, изменяющихся в арифметической прогрессии, определяется следующим образом: 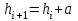 ;в геометрической прогрессии:  ;где а-константа ‑ число, которое будет положительным при прогрессивно возрастающих интервалах и отрицательным при прогрессивно убывающих интервалах; q-константа ‑ положительное число, которое при прогрессивно возрастающих интервалах будет больше 1, а при прогрессивно убывающих - меньше 1. Например, если необходимо построить группировку предприятий отрасли по показателю выручки от реализации продукции, который варьирует от 500 млн. руб. до 4 000 млн. руб., то строить группировку с равными интервалами нецелесообразно, потому что, как правило, совокупность предприятий любой отрасли промышленности, торговли включает большое число малых предприятий, имеющих небольшую выручку. С ростом выручки от реализации продукции значительно снижается число предприятий. Таким образом, распределение числа предприятий по величине выручки является неравномерным. Поэтому следует построить группировку с неравными интервалами (табл. 4.3). Таблица 4.3 ‑ Группировка с неравными интервалами
Величина каждого последующего интервала у этой группировки больше предыдущего на 200 млн. руб., т.е. увеличивается в арифметической прогрессии. При определении границ интервалов статистических группировок исходят из того, что изменение количественного признака приводит к появлению нового качества. В этом случае граница интервала устанавливается там, где происходит переход от одного качества к другому. Рамки границ зависят от условий места и времени. Например, группировка предприятий по числу занятых показывает, что в промышленности и строительстве предприятия со среднесписочной численностью работающих 75-100 человек относятся к группе малых предприятий, а в отраслях непроизводственной сферы и в розничной торговле - к крупным. Поэтому, строя такую группировку, следует дифференцированно устанавливать границы интервалов для разных отраслей народного хозяйства. Это достигается путем использования группировок со специализированными интервалами. Специализированными называются интервалы, применяющиеся для выделения из совокупности одних и тех же типов по одному и тому же признаку для явлений, находящихся в различных условиях. При изучении социально-экономических явлений на макроуровне часто применяют группировки, интервалы которых не будут ни прогрессивно возрастающими, ни прогрессивно убывающими. Такие интервалы называются произвольными. Например, при обработке материалов переписи населения 1989 г. для группировки семей и одиночек по размеру жилой площади, приходящейся на одного человека (м2), применялись следующие группы: до 5; 5 - 6; 7 - 8; 9 - 12; 13-14; 15 - 19; 20 и более. Произвольные интервалы часто используются при группировке рабочих по выработке продукций, предприятий по уровню рентабельности. Группировка с произвольными интервалами может быть построена с помощью коэффициента вариации, определяемого по формуле: 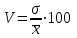 .Построение группировки этим методом начинается с упорядочения единиц совокупности по возрастанию или убыванию группировочного признака. В полученном ряду значений признака первые его значения объединяются в группу до тех пор, пока исчисленный для этой группы коэффициент вариации не станет равен 33%. Это будет свидетельствовать об образовании первой группы, которая исключится из исходной совокупности. Оставшаяся ее часть принимается за новую совокупность, для которой повторяется алгоритм образования новой группы. И так до тех пор, пока все единицы совокупности не будут объединены в группы. Вариационный ряд, состоящий из двух граф (варианты и частоты), иногда дополняется другими графами, необходимыми для вычисления отдельных статистических показателей или для более отчетливого выражения характера вариации изучаемого признака. Достаточно часто в ряд вводится графа, в которой подсчитываются накопленные частоты (S). Накопленные частоты показывают, сколько единиц совокупности имеют значение признака не больше, чем данное значение, и исчисляются путем последовательного прибавления к частоте первого интервала частот последующих интервалов. Частоты ряда (f) могут быть заменены частостями (w), которые представляют собой частоты, выраженные в относительных числах (долях или процентах) и рассчитанные путем деления частоты каждого интервала на их общую сумму, т. е.  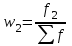 и т. д.Замена частот частостями позволяет сопоставлять вариационные ряды с различным числом наблюдений. В табл. 4.4 исчислены частости и накопленные частоты. Таблица 4.4 ‑ Выполнение норм выработки рабочими цеха
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
