Тема 4 Стат распределение и их осн характеристики. Тема 4 Статистические распределения и их основные характеристики 1 Ряды распределения и группировки. Принципы построения статистических группировок
 Скачать 233.87 Kb.
|
Показатели формы распределенияДля получения приблизительного представления о форме распределения строят графики распределения (полигон и гистограмму). В практике статистических исследований приходится встречаться с самыми различными распределениями. Однородные совокупности характеризуются, как правило, одновершинными распределениями. Многовершинность свидетельствует о неоднородности изучаемой совокупности. В этом случае необходима перегруппировка данных с целью выделения более однородных групп. Выяснение общего характера распределения предполагает оценку степени его однородности, а также исчисление показателей асимметрии и эксцесса. Для сравнительного анализа степени асимметрии нескольких распределений рассчитывается относительный показатель асимметрии ( 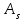 ): 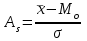.Величина показателя асимметрии 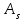может быть положительной и отрицательной. Положительная величина показателя асимметрии указывает на наличие правосторонней асимметрии. Отрицательный знак показателя асимметрии говорит о наличии левосторонней асимметрии. Чем больше абсолютная величина коэффициента, тем больше степень скошенности. 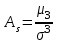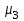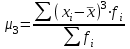Принято считать, что если коэффициент асимметрии меньше 0,25, то асимметрия незначительная, если свыше 0,5, то асимметрия значительная.Наиболее распространенным является показатель асимметрии, исчисляемый по формуле:  где  - центральный момент третьего порядка; Этот показатель асимметрии не только определяет степень асимметрии, но и указывает на наличие или отсутствие асимметрии в распределении признака в генеральной совокупности. Оценка степени существенности этого показателя дается с помощью средней квадратической ошибки, рассчитываемой по формуле: 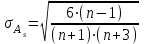 ,где n - число наблюдений. 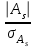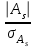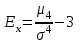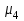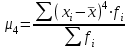Если  > 3 асимметрия существенна и распределение признака в генеральной совокупности не является симметричным.Если < 3 асимметрия несущественна, ее наличие объясняется влиянием случайных обстоятельств.Для симметричных распределений рассчитывается показатель эксцесса (островершинности):  ,где  - центральный момент четвертого порядка; Эксцесс может быть положительным и отрицательным. У высоковершинных распределений показатель эксцесса имеет положительный знак (+), а у низковершинных - отрицательный знак (-). Предельным значением отрицательного эксцесса является значение Ех = (- 2); величина положительного эксцесса является величиной бесконечной. В нормальном распределении 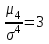 .4.1. По приведенным ниже данным о квалификации рабочих цеха требуется: 1) построить дискретный ряд распределения; 2) дать графическое изображение ряда; 3) вычислить показатели центра распределения, показатели вариации и формы распределения. Тарифные разряды 24 рабочих цеха: 4; 3; 6; 4; 4; 2; 3; 5; 4; 4; 5; 2; 3; 4; 4; 5; 2; 3; 6; 5; 4; 2; 4; 3. 4.2. Имеются следующие данные о возрастном составе рабочих цеха (лет): 18; 38; 28; 29; 26; 38; 34; 22; 28; 30; 22; 23; 35; 33; 27; 24; 30; 32; 28; 25; 29; 26; 31; 24; 29; 27; 32; 25; 29; 29. Для анализа распределения рабочих цеха по возрасту требуется: 1) построить интервальный ряд распределения; 2) дать графическое изображение ряда; 3) исчислить показатели центра распределения, показатели вариации и формы распределения. Сформулировать вывод. 4.3. Имеются следующие данные о времени простоя автомобиля под разгрузкой:
Проверить закон сложения дисперсий. 4.4. Имеются следующие данные о результатах обследования рабочих предприятия по размеру месячной заработной платы:
Общая дисперсия заработной платы в обследованной совокупности рабочих составила 450. Определить, в какой степени вариация заработной платы рабочих предприятия зависит от возраста. 4.5. Удельный вес основных рабочих в трех цехах предприятия составил: 80, 75 и 90% общей численности рабочих. Определить дисперсию и среднее квадратическое отклонение доли основных рабочих по предприятию в целом, если численность всех рабочих трех цехов составила соответственно 100, 200 и 150 человек. 4.6. Дисперсия признака равна 600. Объем совокупности равен 10. Сумма квадратов индивидуальных значений признака равна 6250. Найти среднюю величину. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ 4.7. Имеются следующие данные о размере семьи работников цеха (число человек в семье):
Составить дискретный вариационный ряд. Определить показатели центра распределения, показатели вариации. Дать графическое изображение ряда в виде полигона распределения. Сформулировать краткие выводы. 4.8. Хронометраж операций пайки радиаторов на ремонтном предприятии дал следующие результаты:
Вычислить: а) среднее время пайки радиатора; б) медиану и моду; в) относительный показатель вариации. Дать графическое изображение ряда в виде гистограммы и полигона частот. 4.9. Имеются следующие данные о возрастном составе группы студентов вечернего отделения:
Построить интервальный ряд распределения. Дать его графическое изображение в виде гистограммы и кумуляты. Используя графическое изображение, определить численное значение моды и медианы. 4.10. Имеются следующие данные о распределении продовольственных магазинов региона по размеру товарооборота за месяц:
Требуется вычислить средний месячный размер товарооборота магазинов региона, дисперсию и коэффициент вариации. 4.11. По автотранспортному предприятию, осуществляющему перевозку грузов автомобилями КамАЗ-5320 грузоподъемностью 16 т, имеются следующие данные о весе партий груза (т): 8 11 14 6 10 13 12 16 15 16 16 10 16 13 14 16 16 4 16 14 5 13 11 2 16 8 16 7 14 16 Построить интервальный ряд распределения партий груза по весу. Для построенного ряда вычислить показатели центра распределения и вариации. Сформулировать вывод об использовании автомобилей КамАЗ-5320. 4.12. Выходной контроль качества поступающих комплектующих изделий дал следующие результаты:
Вычислить дисперсию доли брака по каждой поступившей партии. 4.13. Заработная плата 10 рабочих бригады характеризуется следующими данными:
Проверить правило сложения дисперсий и указать, велико ли влияние профессии на различие в уровне заработной платы. 4.14. Имеются следующие данные о часовой интенсивности движения автомобилей на автомагистрали (авт/ч): 140 99 80 140 218 340 92 152 120 130 50 110 130 96 48 36 60 30 86 102 90 210 220 261 282 312 68 80 131 190 Построить интервальный ряд распределения и вычислить: среднее линейное отклонение, дисперсию, среднее квадратическое отклонение и коэффициент вариации. 4.15. Имеются следующие данные о заработной плате рабочих автотранспортного предприятия за январь:
Определить общую дисперсию заработной платы рабочих предприятия, а также сопоставить однородность двух групп рабочих по уровню месячной заработной платы. 4.16. Средняя величина в совокупности равна 15, среднее квадратическое отклонение равно 10. Чему равен средний квадрат индивидуальных значений этого признака? 4.17. Средняя величина признака в совокупности равна 13, а средний квадрат индивидуальных значений этого признака равен 174. Определить коэффициент вариации. 4.18. Дисперсия признака равна 360 000, коэффициент вариации равен 50%. Чему равна средняя величина признака? 4.19. Дисперсия признака равна 25, средний квадрат индивидуальных значений равен 25. Чему равна средняя? 4.20. Определить дисперсию признака, если средняя величина признака равна 2600 единицам, а коэффициент вариации равен 30%. 4.21. Общая дисперсия равна 8,4. Средняя величина признака для всей совокупности равна 13. Средние по группам равны соответственно 10, 15 и 12. Численность единиц в каждой группе составляет 32, 53 и 45. Определить среднюю внутригрупповую дисперсию. 4.22. По группе промышленных предприятий имеются следующие данные:
Определить общую дисперсию объема продукции. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||