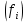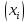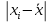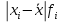Показатели вариации. Закон сложения дисперсий. Уметь выделять абсолютные и относительные показатели Применять закон сложения дисперсий
 Скачать 34.38 Kb. Скачать 34.38 Kb.
|
|
Показатели вариации. Понятие вариации и её виды. Абсолютные показатели вариации. Относительные показатели вариации. Виды дисперсий и закон их сложения. Знать: понятие вариации, её виды. Закон сложения дисперсий. Уметь: выделять абсолютные и относительные показатели Применять закон сложения дисперсий. Владеть: методикой расчета показателей вариации. 1. Понятие вариации и её виды. Рассматривая зарегистрированные в процессе статистического наблюдения величины того или иного признака у отдельных единиц совокупности, можно обнаружить между ними различия. Вариация - это различие в значениях какого- либо признака у разных единиц данной совокупности в один и тот же период или момент времени. Например, работники фирмы различаются по доходам, затратам времени на работу, росту, весу, любимому занятию в свободное время и т.д. Вариация возникает в результате того, что индивидуальные значения признака складываются под совокупным влиянием разнообразных факторов (условий), которые по-разному сочетаются в каждом отдельном случае. Исследование вариации в статистике имеет большое значение, помогает познать сущность изучаемого явления. Измерение вариации, выяснение ее причины, выявление влияния отдельных факторов дает важную информацию (например, о продолжительности жизни людей, доходах и расходах населения, финансовом положении предприятия и т.п.) для принятия научно обоснованных управленческих решений. Средняя величина дает обобщающую характеристику признака изучаемой совокупности, но она не раскрывает строения совокупности, которое весьма существенно для ее познания. Средняя не показывает, как располагаются около нее варианты усредняемого признака, сосредоточены ли они вблизи средней или значительно отклоняются от нее. Средняя величина признака в двух совокупностях может быть одинаковой, но в одном случае все индивидуальные значения отличаются от нее мало, а в другом - эти отличия велики, т.е. в одном случае вариация признака мала, а в другом - велика, это имеет весьма важное значение для характеристики надежности средней величины. Чем больше варианты отдельных единиц совокупности различаются между собой, тем больше они отличаются от своей средней, и наоборот, - чем меньше варианты отличаются друг от друга, тем меньше они отличаются от средней, которая в таком случае будет более реально представлять всю совокупность. Вот почему ограничиваться вычислением одной средней в ряде случаев нельзя. Нужны и показатели, характеризующие отклонения отдельных значений от общей средней. Термин "вариация" произошел от латинского variatio –“изменение, колеблемость, различие”. Однако не всякие различия принято называть вариацией. Под вариацией в статистике понимают такие количественные изменения величины исследуемого признака в пределах однородной совокупности, которые обусловлены перекрещивающимся влиянием действия различных факторов. Вариация существует во времени и пространстве. Под вариацией в пространстве понимается колеблемость значений признака по отдельным территориям. Под вариацией во времени подразумевают изменение значений признака в различные периоды (моменты) времени. Например, с течением времени изменяются средняя продолжительность жизни, цены на различные товары и т.п. Определение вариации необходимо при организации выборочного наблюдения, построении статистических моделей, разработке материалов экспертных опросов и во многих других случаях. Наличие вариации значений признаков изучаемых явлений ставит перед статистикой задачи ее исследования: ─ определение меры вариации, ─ выбор соответствующих измерителей или показателей, характеризующих ее размеры, ─ измерение влияния факторов, ее определяющих. Каким же образом статистика дает количественную оценку степени колеблемости признака в совокупности, измеряет вариацию? В чисто математической части решения этой проблемы общая теория статистики опирается на математическую статистику, в которой излагается математическая сторона таких показателей вариации, как размах вариации, среднее линейное определение, дисперсия, среднее квадратическое отклонение, коэффициент вариации. Однако эти показатели находят широкое применение и в социально-экономической статистике. Далее рассмотрим сущностную и логическую основы этих показателей. 2. Абсолютные показатели вариации. Показатели вариации делятся на две группы: абсолютные и относительные. К абсолютным показателям относятся: - размах вариации - среднее линейное отклонение - дисперсия - среднее квадратическое отклонение. Размах вариации (R) вычисляется как разность между наибольшим и наименьшим значениями варьирующего признака: 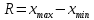 Он показывает, насколько велико различие между единицами совокупности, имеющими самое маленькое (хmin) и самое большое значение признака (хmax). Например, различие между максимальной и минимальной пенсией отдельных групп населения, уровнем дохода различных категорий работающих, стажем работы и т.п. Размах является важной характеристикой вариации, он дает первое общее представление о различии единиц внутри совокупности. Размах вариации выражается в тех именованных числах, в каких выражены значения признака. Особенность показателя размаха вариации заключается в том, что он зависит лишь от двух крайних значений признака. По этой причине его целесообразно применять в тех случаях, когда особое значение имеет либо минимальный, либо максимальный вариант, т. е. когда размах вариации имеет важное смысловое значение. Например, им определяются пределы, в которых могут колебаться размеры тех или иных параметров деталей; его используют при испытании стальных тросов на разрыв и т. п. Другая сторона этой особенности заключается в том, что на величину размаха вариации большое влияние оказывает случайность. Так как из статистического ряда берутся только два значения признака, причем крайние в ряду, на размах этих значений могут оказывать влияние причины случайного характера, то и размах вариации может быть зависимым от случайных причин. С отмеченной особенностью связано и то обстоятельство, что показатель размаха вариации не учитывает частот в вариационном ряду распределения. Показатель размаха вариации дает обобщающую характеристику только границам (амплитуде) значений признака, но не дает характеристики вариации распределению отклонений. Распределение отклонений можно уловить, вычислив отклонения всех вариант от средней. А для того, чтобы дать им обобщающую характеристику, необходимо далее вычислить среднюю из этих отклонений, т. е. разности между значением признака и средней арифметической в данной совокупности единиц. Для этого было предложено рассчитывать такой показатель, как среднее линейное отклонение. Для несгруппированных данных (если каждый вариант в ряду распределения повторяется один раз) среднее линейное отклонение определяется по формуле: 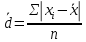 где 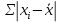 абсолютные значения отклонений отдельных вариантов от их средней величины; абсолютные значения отклонений отдельных вариантов от их средней величины;n — объем совокупности. Для сгруппированных данных формула имеет следующий вид: 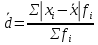 где 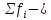 сумма частот вариационного ряда. сумма частот вариационного ряда.Среднее линейное отклонение обладает большим преимуществом перед размахом вариации в отношении полноты характеристики колеблемости признака. Однако при этом в некотором смысле нарушается элементарное правило математики, так как отклонение от среднего значения признака складывается без учета знаков. Это обстоятельство вынуждает искать такой показатель вариации, который был бы лишен и этого недостатка. Хотя в некоторых случаях суммирование показателей без учета знаков имеет экономический смысл. Например, в практической статистике оборот внешней торговли страны определяется как сумма экспорта и импорта, общий оборот рабочей силы — как сумма принятых и уволенных и т. д. Отмеченный выше недостаток среднего линейного отклонения может быть устранен путем возведения в квадрат отклонений вариантов от средней величины. В этом случае возникает понятие следующего показателя вариации – дисперсии. Дисперсия представляет собой средний квадрат отклонения значений признака от их средней величины. Порядок ее вычисления можно выразить следующими формулами. Если данные не сгруппированы, то дисперсия определяется по формуле: 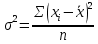 Для сгруппированных данных формула примет вид: 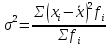 Квадратный корень из дисперсии носит название среднего квадратического отклонения от средней. Для его расчета используют следующие формулы: для несгруппированных данных 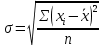 для сгруппированных данных 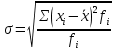 Среднее квадратическое отклонение так же, как и среднее линейное отклонение, показывает, на сколько в среднем отклоняются конкретные значения признака от среднего их значения. Среднее квадратическое отклонение всегда больше среднего линейного отклонения. Среднее квадратическое отклонение измеряет абсолютный размер колеблемости признака и выражается в тех же единицах измерения, что и значения признака (рублях, тоннах, процентах и т. д.). Оно является абсолютной мерой вариации. Дисперсия единицы измерения не имеет. Рассмотрим расчет абсолютных показателей вариации на примере. Имеются данные о распределении населения по уровню среднедушевых денежных доходов.
Величина среднедушевого дохода в среднем по всем группам составит: 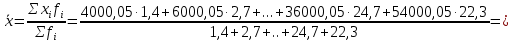 = 29435,55 (руб.). Среднее линейное отклонение составит: 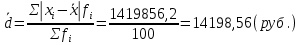 Среднее квадратическое отклонение составит: 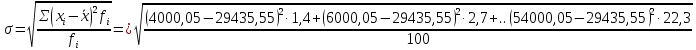 = 16102,95 (руб.). Таким образом, можно сделать вывод, что среднедушевой доход населения по каждой группе отличается от среднего дохода по всем группам (29435,55) в среднем на 16102,95 руб. 3. Относительные показатели вариации. Для целей сравнения колеблемости различных признаков в одной и той же совокупности или при сравнении колеблемости одного и того же признака в нескольких совокупностях, представляют интерес показатели вариации, приведенные в относительных величинах. Базой для сравнения служит средняя арифметическая. Эти показатели вычисляются как отношение размаха вариации, среднего линейного отклонения или среднего квадратического отклонения к средней арифметической. Чаще всего выражаются в процентах и определяют не только сравнительную оценку вариации, но и дают характеристику однородности совокупности. К относительным показателям вариации относятся: - коэффициент осцилляции, - относительное линейное отклонение - коэффициент вариации. Коэффициент осцилляции: 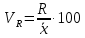 Линейный коэффициент вариации: 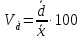 Коэффициент вариации: 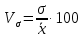 В коэффициентах вариации устраняются не только несопоставимость, связанная с различными единицами измерения изучаемого признака, но и несопоставимость, возникающая вследствие различий в величине средних арифметических. Кроме того, показатели вариации дают характеристику однородности совокупности. Так, чем больше значение коэффициента вариации, тем больше разброс значений признака вокруг средней, тем больше неоднородность совокупности. При этом вопрос о степени интенсивности вариации должен решаться для каждого изучаемого признака индивидуально, исходя из сравнения наблюдаемой вариации с некоторой её обычной интенсивностью, принимаемой за норму. Общепринятым является следующее утверждение: совокупность считается однородной, если коэффициент вариации не превышает 33%. Рассчитаем коэффициент вариации для данных нашего примера: 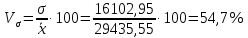 Поскольку полученное значение коэффициента вариации превышает 33%, то можно сделать вывод, что совокупность неоднородна. В нашем случае это означает, что среднедушевой доход по группам населения сильно варьирует. Также можно сказать, что доходы по отдельным группам населения сильно отличаются между собой, то есть, например, в первой группе максимальный доход составляет 5000 руб. (при этом доля населения с таким доходом составляет 1,4%), а в последней группе минимальный доход составляет 45000 руб., и численность населения с такими доходами достаточно велика (более 1/5, или 22,3%). Таким образом, разрыв между доходами этих двух групп в среднем составляет 9 раз. 4. Виды дисперсий и закон их сложения. Наряду с изучением вариации признака по всей совокупности в целом бывает необходимо проследить количественные изменения признака по группам, на которые разделяется совокупность, а также между группами. Такое изучение вариации достигается посредством вычисления и анализа различных видов дисперсии. При этом выделяют три вида дисперсии: общую, внутригрупповую и межгрупповую. Общая дисперсия (σ2) измеряет вариацию признака во всей совокупности под влиянием всех факторов, обусловивших эту вариацию, и рассчитывается по формуле: 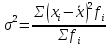 Внутригрупповая дисперсия 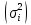 отражает случайную вариацию, то есть часть вариации, происходящую под влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Она вычисляется следующим образом: отражает случайную вариацию, то есть часть вариации, происходящую под влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Она вычисляется следующим образом: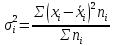 где ni— число единиц в каждой выделенной группе; 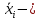 среднее значение признака в i-й группе. среднее значение признака в i-й группе.Средняя из внутригрупповых дисперсий 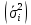 равна: равна: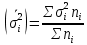 Межгрупповая дисперсия 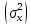 характеризует систематическую вариацию, т. е. различия в величине изучаемого признака, возникающие под влиянием признака-фактора, положенного в основание группировки. Она рассчитывается по формуле: характеризует систематическую вариацию, т. е. различия в величине изучаемого признака, возникающие под влиянием признака-фактора, положенного в основание группировки. Она рассчитывается по формуле: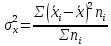 Существует закон, связывающий три вида дисперсий: Общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсий 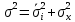 Данное соотношение называется правилом сложения дисперсий. Оно используется в ряде методов статистики, в частности при расчете ошибок выборочного наблюдения и при измерении тесноты связи между признаками. Теоретический и практический интерес этого правила заключается, во-первых, в том, что зная две величины, мы на основе приведенного равенства всегда можем определить третью величину. Второе важное значение этого правила состоит в том, что зная общую дисперсию и дисперсию групповых средних, мы имеем право (если группировка произведена правильно) судить о силе влияния группировочного признака с помощью эмпирического коэффициента детерминации и эмпирического корреляционного отношения. Эмпирический коэффициент детерминации (η2) представляет собой долю межгрупповой дисперсии в общей дисперсии и рассчитывается по формуле: 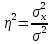 Этот коэффициент показывает долю (удельный вес) общей вариации изучаемого признака, обусловленного вариацией группировочного признака. Эмпирическое корреляционное отношение (η) представляет собой корень квадратный из эмпирического коэффициента детерминации и рассчитывается следующим образом: 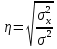 Оно характеризует влияние признака, положенного в основание группировки, на вариацию результативного признака. Эмпирическое корреляционное отношение изменяется в пределах от 0 до 1. Если η = 0, то признак не оказывает влияние на результативный. Если η = 1, то результативный признак изменяется только в зависимости от признака, положенного в основание группировки, а влияние прочих факторных признаков равно нулю. Промежуточные значения оцениваются в зависимости от их близости к предельным значениям. Например. Имеются данные о продолжительности работы малых предприятий и себестоимости единицы продукции, которую они производят:
Проведем оценку тесноты связи между продолжительностью работы малых предприятий, производящих аналогичную продукцию, на рынке и себестоимостью единицы этой продукции. Предваряя расчеты отметим, что для вычисления необходимых показателей будут использованы формулы простых средних и показателей вариации, поскольку частоты в каждой группе предприятий представлены в виде данных по отдельным единицам (т.е. не сгруппированы). 1. Определим среднюю себестоимость продукции по каждой группе предприятий: 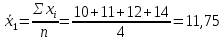 (руб.) (руб.)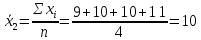 (руб.) (руб.)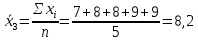 (руб.) (руб.)2. Определим среднюю себестоимость единицы продукции по всем предприятиям: 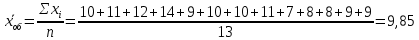 (руб.) (руб.)3. Определим внутригрупповые дисперсии: 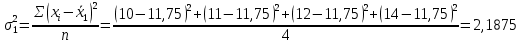 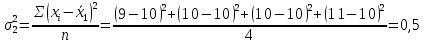 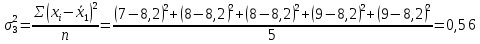 4. Определим среднюю из внутригрупповых дисперсий: 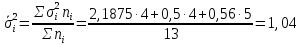 Определим межгрупповую дисперсию: 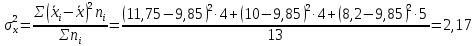 Определим общую дисперсию по общей формуле: 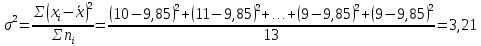 Проверим правило сложения дисперсий: общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсий 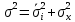 3,21 = 1,04 + 2,17 8. Рассчитаем эмпирический коэффициент детерминации: 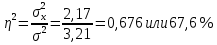 Чем больше доля межгрупповой дисперсии в общей дисперсии, тем сильнее влияние группировочного признака (продолжительности работы на рынке) на изучаемый признак (себестоимость единицы продукции). Таким образом, вариация себестоимости единицы продукции на 67,6% обусловлена продолжительностью работы предприятий на рынке и на 32,4% действием прочих факторов. 9. Рассчитаем эмпирическое корреляционное отношение (характеризующее тесноту связи между группировочным и результативным признаком): 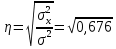 =0,822 =0,822Поскольку эмпирическое корреляционное отношение находится в пределах от 0 до 1, то можно сказать, что связь между группировочным признаком (продолжительность работы на рынке) и результативным признаком (себестоимостью единицы продукции) достаточно сильная. Дисперсия альтернативного (качественного) признака. В статистике наряду с показателями вариации количественного признака определяются показатели вариации альтернативного признака. Альтернативными являются признаки, которыми обладают одни единицы совокупности и не обладают другие. Например, работники предприятия по полу подразделяются на мужчин и женщин, т.е. в данном случае это два взаимоисключающих варианта. При статистическом выражении колеблемости альтернативных признаков наличие изучаемого признака обозначается 1, а его отсутствие – 0. Доля вариантов, обладающих изучаемым признаком, обозначается p, а доля вариантов, не обладающих признаком, обозначается q . Следовательно, p + q = 1 Найдем их среднее значение: 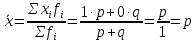 Найдем дисперсию альтернативного признака: 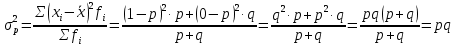 Например. Население района составляет 10 000 чел., в том числе 4 000 мужчины, 6 000 женщины. Доля мужчин составляет p = 4 000 / 10 000 = 0,4 Доля женщин = 6 000 / 10 000 = 0,6 Дисперсия составит = 0,4 · 0,6 = 0,24. При расчете показателей дисперсии по альтернативному признаку сумма p + q не может быть больше 1, а их произведение не может быть больше 0,25 (0,5 ·0,5). |