Тема 4 Стат распределение и их осн характеристики. Тема 4 Статистические распределения и их основные характеристики 1 Ряды распределения и группировки. Принципы построения статистических группировок
 Скачать 233.87 Kb. Скачать 233.87 Kb.
|
4.2 Графическое изображение вариационного рядаПервым этапом изучения вариационного ряда является его графическое изображение. Дискретный вариационный ряд изображается в виде так называемого полигона, или многоугольника, распределения частот, являющегося разновидностью статистических ломаных. Для изображения интервального ряда применяются полигон распределения частот и гистограмма частот. Строятся графики в прямоугольной системе координат. При построении полигона частот на оси абсцисс в одинаковом масштабе откладываются направо в порядке возрастания значения признака (для дискретного характера) или центральные значения интервалов (для интервальных рядов); по оси ординат наносится шкала для выражения величин частот. Из точек на оси абсцисс, соответствующих величине признака, восстанавливаются перпендикуляры высотой, соответствующей частоте; вершины перпендикуляров соединяются отрезками прямой. Крайние точки полученной ломаной соединяются с лежащими на оси абсцисс следующими (меньшими и большими) возможными, но фактически не наблюдающимися значениями признака, частота которых, очевидно, равна 0. Замкнутая с осью абсцисс ломаная линия представляет полигон распределения частот. Построим полигон частот по табл. 4.4. (рис.4.1) 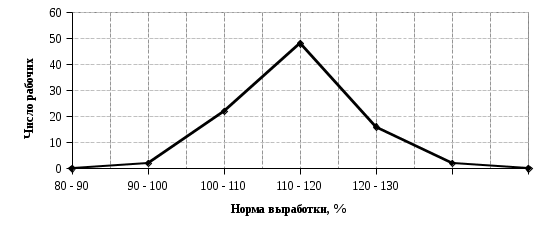 Рис. 4.1 – Полигон распределения рабочих по выполнению норм выработки Для построения гистограммы по оси абсцисс откладывают величины интервалов, а частоты изображаются прямоугольниками, построенными на интервалах с высотой в масштабе оси ординат (рис. 4.2). В случае неравенства интервалов гистограмма строится не по частотам или частостям, а по плотности распределения. 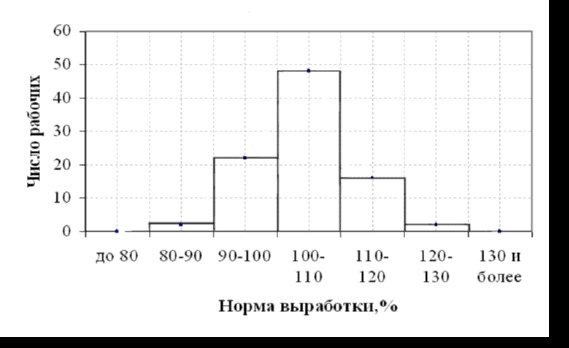 Рис. 4.2 – Гистограмма распределения рабочих по выполнению норм выработки В ряде случаев для изображения вариационных рядов используется кумулятивная кривая (кумулята (рис.4.3), она особенно удобна для сравнения вариационных рядов. Накопленные частоты наносятся на чертеж в виде ординат; соединяя вершины отдельных ординат прямыми, получают ломаную линию, которая, начиная с нуля, непрерывно поднимается над осью абсцисс, до тех пор пока не достигнет высоты, соответствующей общей сумме частот. 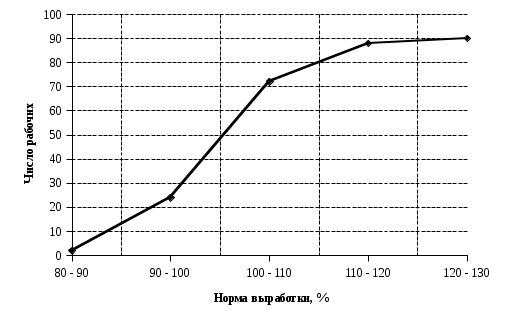 Рис. 4.3 – Кумулята распределения рабочих по выполнению норм выработки Если поменять местами оси координат в кумуляте, то получаем новый вид графического изображения - огиву. При построении графических изображений вариационного ряда большое значение имеет соотношение масштабов по оси абсцисс (х) и оси ординат (f). В этом случае следует руководствоваться так называемым «правилом золотого сечения», в соответствии с которым высота графика должна быть примерно в два раза меньше его основания. 4.3 Анализ вариационных рядовДля анализа вариационных рядов используются три группы показателей: показатели центра распределения; показатели степени вариации; показатели формы распределения. Показатели центра распределенияДля характеристики среднего значения признака в вариационном ряду применяются: средняя арифметическая, медиана, мода. Средняя арифметическая для дискретного ряда распределения исчисляется по формуле: 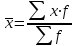 , ,где х - варианты значений признака; f - частота повторения данного варианта. Средняя арифметическая для интервального ряда распределения: 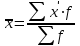 , ,где х' - середина соответствующего интервала значения признака. Медиана (Me) соответствует варианту, стоящему в середине ранжированного ряда. Положение медианы определяется ее номером: 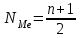 , ,где n — число единиц в совокупности. По накопленным частотам определяют ее численное значение в дискретном вариационном ряду. В интервальном ряду распределения сначала указывают интервал, в котором находится медиана. Медианным является первый интервал, в котором сумма накопленных частот превысит половину общего числа наблюдений. Численное значение медианы определяется по формуле: 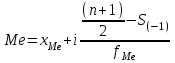 , ,где 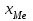 - нижняя граница медианного интервала; - нижняя граница медианного интервала;i - величина интервала; S(-1) - накопленная частота интервала, предшествующего медианному; f- частота медианного интервала. Мода (Мо) - наиболее часто встречающееся значение признака. В дискретном ряду - это варианта с наибольшей частотой. В интервальном ряду сначала определяется модальный интервал, т. е. тот интервал, который имеет наибольшую частоту. Конкретное значение моды определяется по формуле: 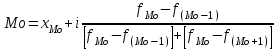 , ,где 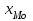 - нижняя граница модального интервала; - нижняя граница модального интервала;fMo- частота модального интервала; f(Mo-1) - частота интервала, предшествующего модальному; f(Mo+1) - частота интервала, следующего за модальным. Моду и медиану можно определить на основе графического изображения ряда. Медиана определяется по кумуляте. Для ее определения высоту наибольшей ординаты, которая соответствует общей численности, делят пополам. Через полученную точку проводят прямую, параллельную оси абсцисс, до пересечения ее с кумулятой. Абсцисса точки пересечения является медианной величиной. Мода определяется по гистограмме распределения. Для этого правую вершину модального прямоугольника соединяют с правым верхним углом предыдущего прямоугольника, а левую вершину модального прямоугольника - с левым верхним углом последующего прямоугольника. Абсцисса точки пересечения этих прямых и будет модой распределения. |
