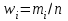Главная страница
Навигация по странице:

  • Технология решения задач на составление вариационного ряда, графическое изображение данных, нахождение характеристик вариационного ряда

    		•

    Задачи на составление вариационного ряда, графическое изображени. Алгоритм решения задач на первичную обработку статистических данных


    Скачать 84.79 Kb.
    НазваниеАлгоритм решения задач на первичную обработку статистических данных
    Дата31.05.2022
    Размер84.79 Kb.
    Формат файлаdocx
    Имя файлаЗадачи на составление вариационного ряда, графическое изображени.docx
    ТипДокументы
    #558661


    Алгоритм решения задач на первичную обработку статистических данных




    Найти размах R, моду M0, медиану Me, среднюю арифметическую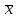





    Технология решения задач на составление вариационного ряда, графическое изображение данных, нахождение характеристик вариационного ряда


    Из генеральной совокупности с дискретным изменением признака X произведена выборка объема n=50, записанная в виде первоначальной таблицы. Произвести первичную статистическую обработку данных

    70
    80
    85
    95
    80
    85
    80
    95
    90
    80

    100
    90
    80
    70
    90
    75
    100
    85
    75
    95

    80
    70
    100
    85
    70
    85
    90
    75
    85
    75

    75
    95
    90
    80
    85
    80
    85
    85
    80
    100

    85
    90
    85
    95
    90
    95
    75
    85
    85
    85





    Решение

    1.Составим вариационный ряд. Вариационным рядом называется последовательность вариантов, записанных в порядке их возрастания (убывания), причем одинаковые варианты записываются столько раз, сколько раз они встречаются в статистической совокупности.

    70
    70
    70
    70
    75
    75
    75
    75
    75
    75

    80
    80
    80
    80
    80
    80
    80
    80
    80
    85

    85
    85
    85
    85
    85
    85
    85
    85
    85
    85

    85
    85
    85
    85
    90
    90
    90
    90
    90
    90

    90
    95
    95
    95
    95
    95
    100
    100
    100
    100




    1. Составим таблицу распределения частот и частостей. Частотой варианта называется число, показывающее, сколько раз встречается данный вариант в статистической совокупности. Частостью (относительной частотой) варианта называется отношение его частоты к объему выборки. В первой строке таблицы запишем различные варианты; во второй – соответствующие им частоты.


    xi
    70
    75
    80
    85
    90
    95
    100

    mi
    4
    6
    9
    15
    7
    5
    4



    4/50=0,08
    0,12
    0,18
    0,30
    0,14
    0,10
    0,08

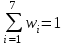    3. Построим полигон частостей. Полигоном частот (частостей) дискретного вариационного ряда называется ломаная, соединяющая последовательно точки (xi; mi) (или (xi; wi)).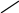


    0

    70 75 80 85 90 95 100

    xi

    0,30


    0,18

    0,14

    0,12

    0,10

    0,08


    wi



        1. Запишем эмпирическую функцию распределения и построим ее график.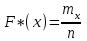

    ,где mx – число вариант, меньших x; n – объем выборки.


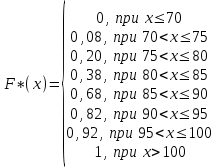    График функции F*(x) имеет вид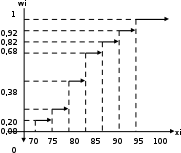



        1. .Размах – разность между наибольшим и наименьшим вариантами статистической совокупности R=xнаиб – xнаим ,

    где xнаим = 70; xнаиб = 100; R = 100 – 70 = 30; R = 30.

    Мода – вариант вариационного ряда с наибольшей частотой. Мода М0 = 85, т.к. m4=15 – наибольшая частота.

    Медиана – вариант, делящий вариационный ряд на две равные по числу вариант части.

    Если n=2k – четное число, то медиана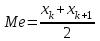

    .
    Если n=2k+1 – нечетное число, то медиана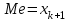

    .

    Для нашей задачи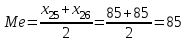

    .
    Средняя арифметическая находится по формуле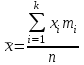

    .

    Для нашей задачи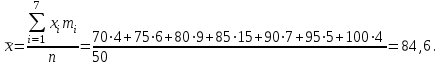

    написать администратору сайта