Линейная алгебра. Лин. алгебра 1. Решение а Решим систему методом Гаусса Запишем расширенную матрицу систему
 Скачать 210.32 Kb. Скачать 210.32 Kb.
|
|
Задача 1 Решить неоднородную систему линейных уравнений: а) методом Гаусса; б) методом Крамера; б) матричным методом. 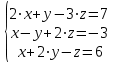 Решение: а) Решим систему методом Гаусса Запишем расширенную матрицу систему: 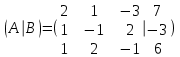 Приведем расширенную матрицу системы к треугольному виду: поменяем местами первую и вторую строки: 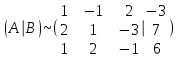 умножим первую строку на (-2) и сложим со второй, затем умножим первую строку на (-1) и сложим с третьей 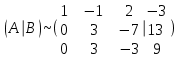 разделим третью строку на 3 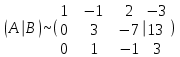 поменяем местами вторую и третью строки 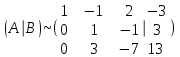 умножим вторую строку на (-3) и сложим с третьей 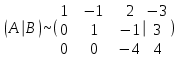 разделим третью строку на -4 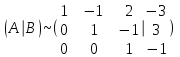 Система примет вид: 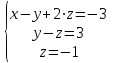 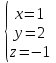 б) Решим систему методом Крамера. Запишем определитель системы и вычислим его разложением по первой строке: 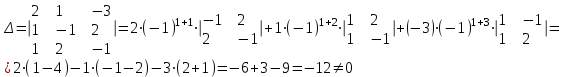 Следовательно, система имеет единственное решение. Вычислим вспомогательные определители, также воспользовавшись правилом разложения по первой строке: 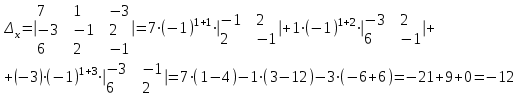 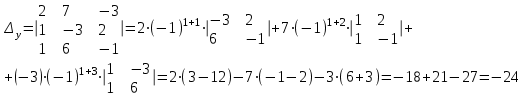 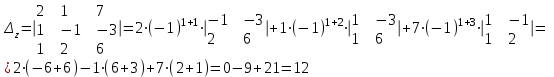 Найдем решение системы: 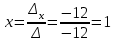 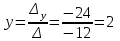 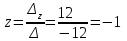 в) Найдем решение системы методом обратной матрицы Запишем систему в матричной форме: А·Х=В, где 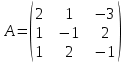 - матрица коэффициентов системы - матрица коэффициентов системы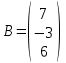 - столбец свободных членов - столбец свободных членов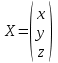 - решение системы - решение системыХ=А-1·В Найдем обратную матрицу А-1 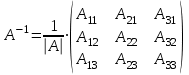 , где Аij - алгебраические дополнения элементов матрицы А , где Аij - алгебраические дополнения элементов матрицы АНайдем определитель матрицы А: 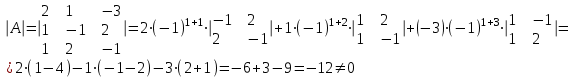 Найдем алгебраические дополнения: 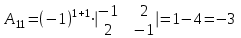 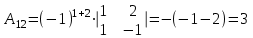 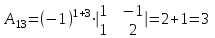 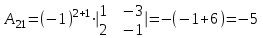 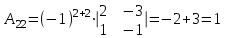 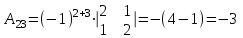 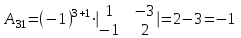 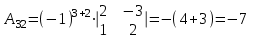 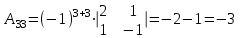 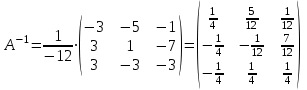 Найдем Х 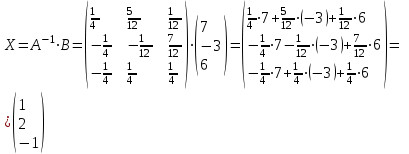 Задача 2 Даны координаты вершин пирамиды АВСD. Требуется: 1) скалярное произведение 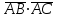 ; ;2) длины сторон 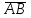 и и 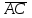 ; ;2) найти угол между этими сторонами 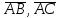 4) найти площадь грани АВС; 5) найти объем пирамиды АВСD А(1;1;1), В(6;3;1), С(3;6;1), D(2;3;5) Решение: 1) Найдем координаты векторов: 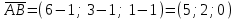 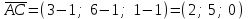 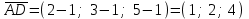 Найдем длины векторов: 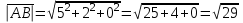 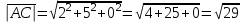 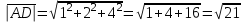 2) Найдем скалярное произведение векторов 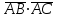 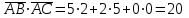 3) Найдем угол между векторами 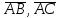 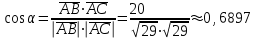 460 4) Найдем площадь грани АВС 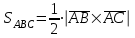 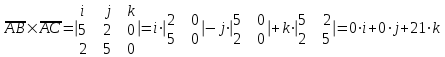 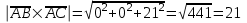 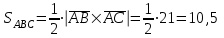 5) Найдем объем пирамиды АВСD 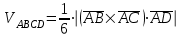 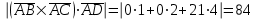 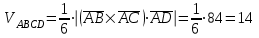 Задача 3 Даны координаты вершин треугольника АВС. Построить на плоскости ХОУ точки А, В,С по их координатам. Затем а) написать уравнения прямых АВ и АС; б) вычислить угол между этими прямыми через их угловые коэффициенты; в) написать уравнение высоты, опущенной из вершины В на сторону АС;; г) найти длину высоты, опущенной из вершины В на сторону АС А(11;-15), В(6;-3), С(-2;-9) Решение: Чертеж треугольника 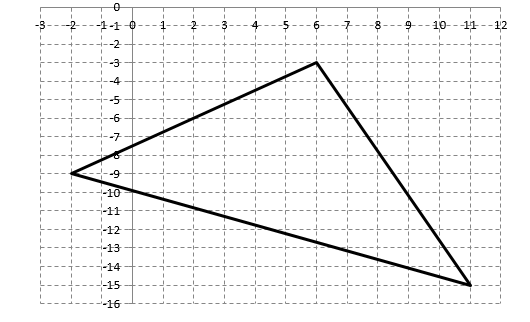 А В С а) Составим уравнение прямой АВ по точкам А(11;-15), В(6;-3) 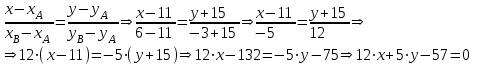 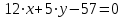 - общее уравнение прямой АВ - общее уравнение прямой АВЗапишем уравнение АВ в виде с угловым коэффициентом, т.е. в виде 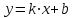 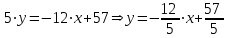 - уравнение АВ в виде с угловым коэффициентом, где - уравнение АВ в виде с угловым коэффициентом, где 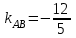 Составим уравнение прямой АC по точкам А(11;-15), С(-2;-9) 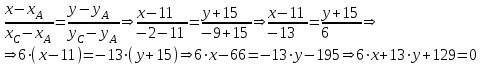 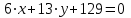 - общее уравнение прямой АC - общее уравнение прямой АCЗапишем уравнение ВC в виде с угловым коэффициентом 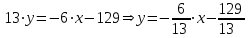 - уравнение АC в виде с угловым коэффициентом, где - уравнение АC в виде с угловым коэффициентом, где 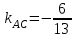 б) Найдем угол между прямыми АВ и АС 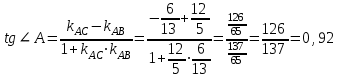 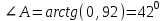 в) Составим уравнение высоты ВD по точке В(6;-3) и угловому коэффициенту 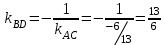 , т.к. , т.к. 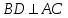 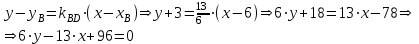 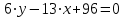 - общее уравнение высоты ВD - общее уравнение высоты ВDг) Длину высоты ВD найдем как расстояние от точки В(6;-3) до прямой АС 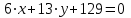 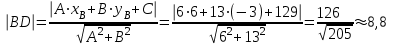 Задача 4 Используя данные задачи 2: а) написать уравнение плоскости, проходящей через точку А перпендикулярно стороне ВС; б) написать уравнение грани АВС; в) написать уравнение прямой, проходящей через точки С и D, перейти от канонического задания этой прямой к е параметрическому заданию; г) найти точку пересечения этой прямой с плоскостью 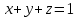 А(1;1;1), В(6;3;1), С(3;6;1), D(2;3;5) Решение: а) Составим уравнение плоскости по точке А(1;1;1) и нормальному вектору 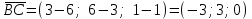 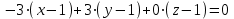 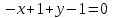 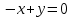 уравнение заданной плоскости уравнение заданной плоскостиб) Составим уравнение плоскости АВС по точке А(1;1;1) и нормальному вектору 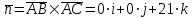 , , 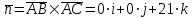 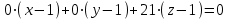 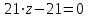 уравнение плоскости АВС уравнение плоскости АВСв) Составим уравнение прямой СD по точкам С(3;6;1) и D(2;3;5) 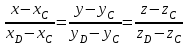 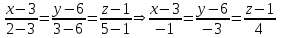 - уравнение прямой СD - уравнение прямой СD Запишем уравнение прямой СD в параметрической форме: 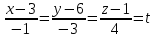 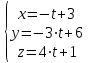 уравнение прямой в параметрической форме, где tR уравнение прямой в параметрической форме, где tRг) Найдем точку пересечения прямой СD с плоскостью 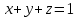 Подставим в уравнение плоскости 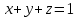 параметрическое задание прямой параметрическое задание прямой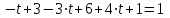 не выполняется при любых tR, т.е. нет точки пересечения заданной прямой и плоскости. не выполняется при любых tR, т.е. нет точки пересечения заданной прямой и плоскости.Задача 5 Найти собственные числа и собственные векторы матрицы 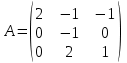 Решение: Составим характеристическое уравнение: 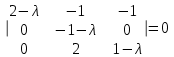 , найдем корни характеристического уравнения , найдем корни характеристического уравнения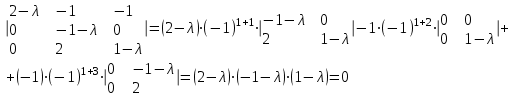 Корни 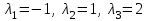 Получаем собственные числа матрицы 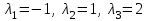 Найдем собственные векторы матрицы: 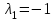 Составим систему уравнений: 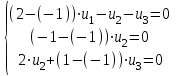 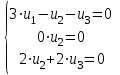 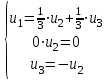 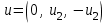 , где , где 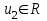 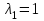 Составим систему уравнений: 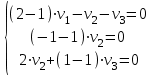 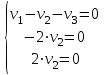 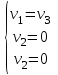 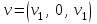 , где , где 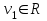 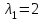 Составим систему уравнений: 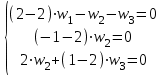 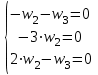 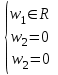 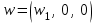 |
