контрольная работа по мат.анализу 1 курс 3 вариант. математика 3 вариант канашский универ. Контрольная работа 1 По математике Вариант 3 Студента 1 курса экономического факультета Шифр 04653033 Учебная группа 5306
 Скачать 0.57 Mb. Скачать 0.57 Mb.
|
|
Канашский филиал КОНТРОЛЬНАЯ РАБОТА № 1 По математике Вариант 3 Студента 1 курса экономического факультета Шифр: 04653033 Учебная группа: 53-06 Работа выслана в Чувашский госуниверситет «____» ____________2006 г. Передана на кафедру «Экономики и управления» Оценка___________ «___» _____________2006г. Преподаватель: Бычков Владимир Порфирьевич Возвращена в деканат______________________ Математика Вариант 3 Даны вершины А(х1;у1) ,В(х2;у2), С(х3;у3) треугольника. Требуется найти: 1)длину стороны ВС; 2)площадь треугольника; 3)уравнение стороны ВС; 4)уравнение высоты проведенной из вершины А; 5)длину высоты проведенной из вершины А; 6)уравнение биссектрисы внутреннего угла 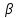 ; ; 7)угол 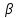 в радианах с точностью до 0,01; 8)систему неравенств определяющих множество точек треугольника. Сделать чертеж. в радианах с точностью до 0,01; 8)систему неравенств определяющих множество точек треугольника. Сделать чертеж.вариант 3: А(5;-1), В(1;-4), С(-4;8). Решение: 1)Длина стороны ВС: 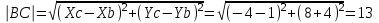  ; ;2)Длина стороны АВ: 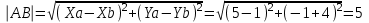 ; ;Скалярное произведение векторов 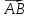 и и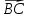 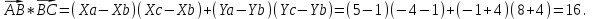 Угол 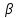 : : cos cos 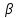 = =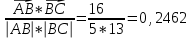 ; ; 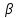 =arcos 0,2462=75,75 =arcos 0,2462=75,75 ; ;3) Уравнение стороны ВС: 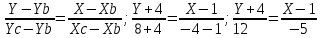 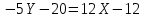 ; ; 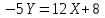 ; ; 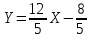 ; ; 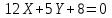 ; ; 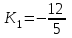 ; ;4) Уравнение высоты, проведенной из вершины А: 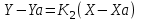 ; ; 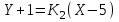 ; ;Условие перпендикулярности двух прямых: 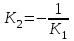 ; ; 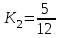 ; ;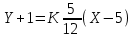 ; ; 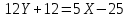 ; ; 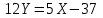 ; ; 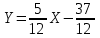 ; ;5) Длина высоты, проведенной из вершины А: 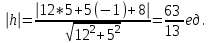 6) 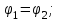 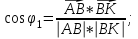 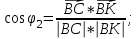 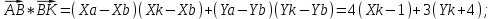 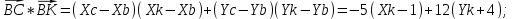 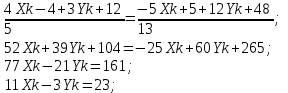 Уравнение прямой АС: 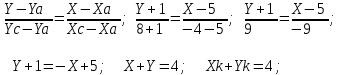 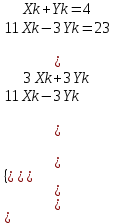 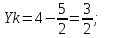 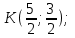 Уравнение биссектрисы внутреннего угла 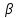 : :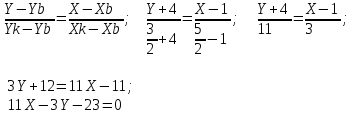 7) Угол 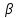 в радианах с точностью до 0,01: в радианах с точностью до 0,01: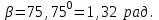 8) Уравнение стороны ВС: 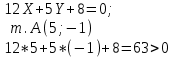 Уравнение стороны АС: 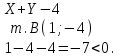 Уравнение стороны АВ: 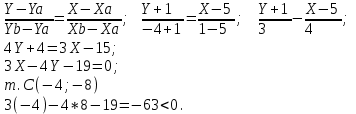 Система неравенств, определяющих множество внутренних точек треугольника. 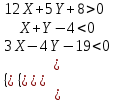 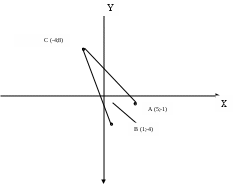  Задание 13. Задание 13.Составить уравнение прямой, проходящей через точку А(4;1) на расстоянии 4 единиц от точки В(-4;0). Решение: Уравнение пучка прямых, проходящих через точку А: 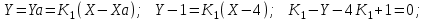 По условию задачи 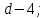 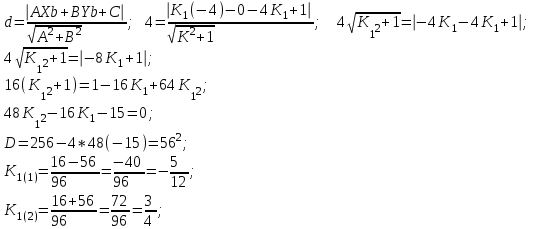 Искомые прямые: 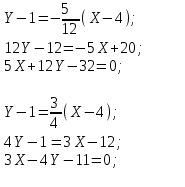 Задание 23. Составить уравнение линии, расстояние каждой точки которой от точки F(8;0) вдвое больше, чем от прямой Х-2=0. Сделать чертеж. Решение: 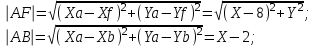 По условию задачи: 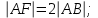 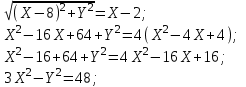 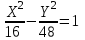 - уравнение гиперболы с центром в точке - уравнение гиперболы с центром в точке 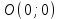 и полуосями и полуосями 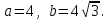  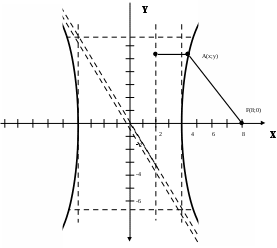 Задание 33. Составить уравнение параболы и ее директрисы, если известно что парабола проходит через точки пересечения прямой 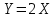 с окружностью с окружностью 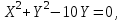 и ось и ось 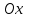 является осью симметрии параболы. Сделать чертеж. является осью симметрии параболы. Сделать чертеж.Решение. Рассмотрим уравнение окружности: 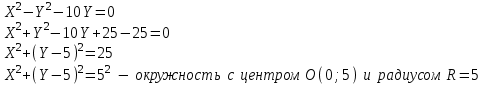 Найдем точки пересечения окружности и прямой. 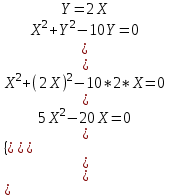 Координаты точек пересечения окружности и прямой 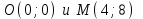 т.к. парабола симметрична относительно ОХ, то уравнение имеет вид т.к. парабола симметрична относительно ОХ, то уравнение имеет вид 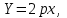 учитывая что учитывая что 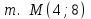 найдем параметр p найдем параметр p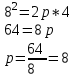 Таким образом, уравнение параболы 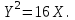 Уравнение директрисы параболы: 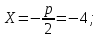 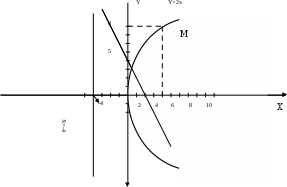 Задание 43. Дано уравнение параболы f(x;y)=0. Сделать параллельный перенос осей координат так, чтобы в новой системе координат XO1Yуравнение параболы приняло вид X2=aY или Y2=aX. Построить обе системы координат и параболу. 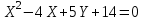 Решение: 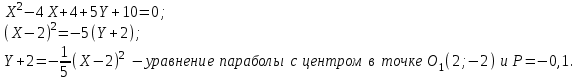 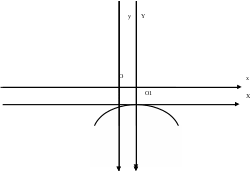 Задание 53 Даны вершины А1(Х1;Y1;Z1),. А2(Х2;Y2;Z2), А3(Х3;Y3;Z3), А4(Х4;Y4;Z4) пирамиды. Требуется найти: 1) длину ребра А1А2; 2)Угол между ребрами А1А2 и А1А4; 3)угол между ребром А1А2и гранью А1А2 А3; 4) площадь грани А1А2 А3; 5) объем пирамиды; 6) уравнение высоты, опущенной из вершины А4на грань А1А2 А3; 7) уравнение плоскости, проходящей через высоту пирамиды, опущенной из вершины А4 на грань А1А2 А3, и вершину А1пирамиды. A1(3;5;4), А2(5;8;3), А3(1;9;9), A4(6;4;8); Решение: 1) 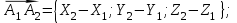 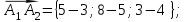 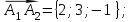 Длина ребра А1А2; 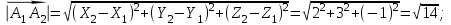 2) 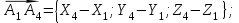 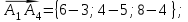 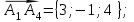 Длина ребра А1А4; 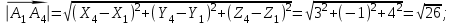 Скалярное произведение векторов А1А2 и А1А4: 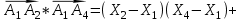 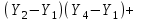 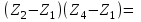 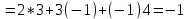 Угол между ребрами А1А2 и А1А4: 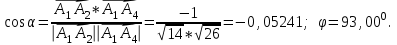 3) Уравнение грани А1А2 А3: 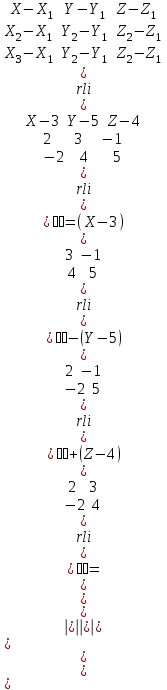 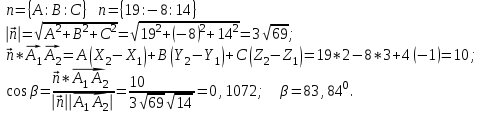 Угол между ребром А1А2и гранью А1А2 А3: 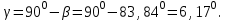 4)Площадь грани А1А2А3: 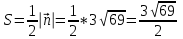 кв. ед. кв. ед.5) Объем пирамиды: 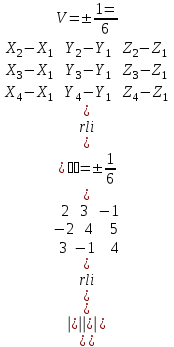 куб. ед. куб. ед.6) уравнение высоты, опущенной из вершины А4на грань А1А2 А3: 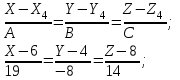 7) Уравнение плоскости, проходящей через высоту пирамиды, опущенной из вершины А4 на грань А1А2 А3, и вершину А1пирамиды. 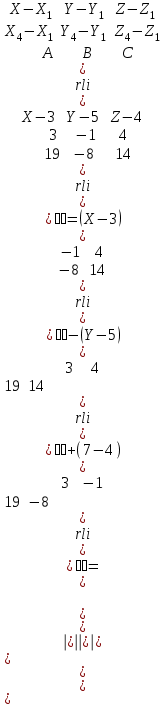 Задание 63. Определить вид поверхности, заданной уравнением f(x;y;z)=0, и показать её расположение относительно системы координат. 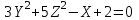 Решение: 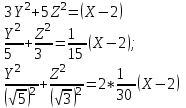 Эллиптический параболоид с вершиной О(z;o;o), направленный вдоль оси ОХ, и имеющий полуоси на оси 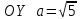 по оси по оси 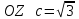 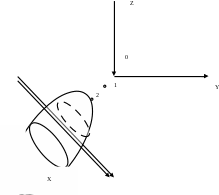 Задание 73. Применяя метод исключения неизвестных, решить систему уравнений. 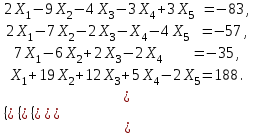 Решение:
Общее решение системы: 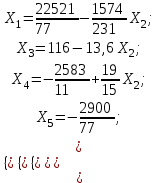 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
