контрольная работа по мат.анализу 1 курс 3 вариант. математика 3 вариант канашский универ. Контрольная работа 1 По математике Вариант 3 Студента 1 курса экономического факультета Шифр 04653033 Учебная группа 5306
 Скачать 0.57 Mb. Скачать 0.57 Mb.
|
|
Задание 83. Даны векторы 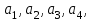 и и 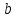 . Показать, что векторы . Показать, что векторы 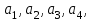 образуют базис четырехмерного пространства, и найти координаты вектора образуют базис четырехмерного пространства, и найти координаты вектора 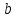 в этом базисе. в этом базисе.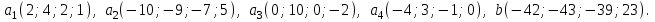 Решение: Составим определитель из координат векторов 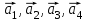 и вычислим его: и вычислим его: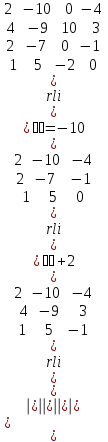 Так как 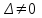 ,то векторы ,то векторы 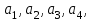 составляют базис. Найдем координаты вектора составляют базис. Найдем координаты вектора 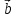 в этом базисе: в этом базисе: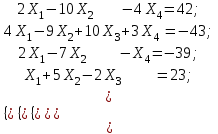
Итак 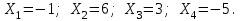 Проверка: 2(-1)-10*6 -4(-5)=-42; -42=-42; 4(-1)-9*6+10*3+3(-5)=-43; -43=-43; 2(-1)-7*6- -(-5)=-39; -39=-39; -1+5*6-2*3 =23; 23=23. 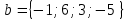 или или 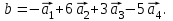 Задание 93. Дана матрица А . Требуется найти: 1) матрицу, обратную матрице А; 2) собственные значения и собственные векторы матрицы А. 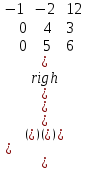 Решение:
Обратная матрица: 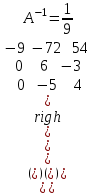 Корни характеристического уравнения: 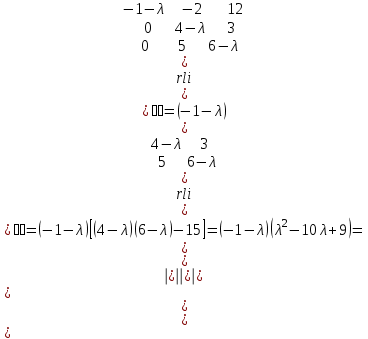 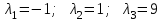 - собственные значения матрицы А . - собственные значения матрицы А .При 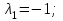 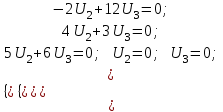 Собственный вектор: 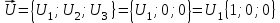 Задание 103. Построить график функции y=f(x) деформацией и сдвигом графика функции y=sinx. 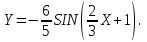 Решение: 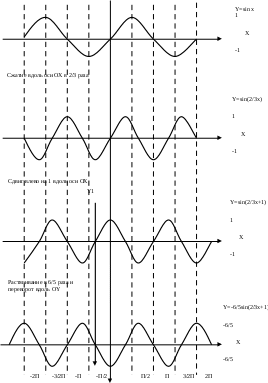 Задание 113. Найти указанные пределы (не пользуясь правилом Лопиталя). 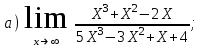 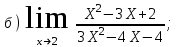 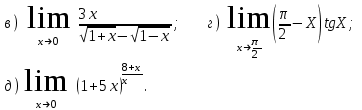 Решение: 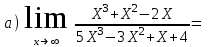 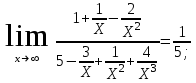 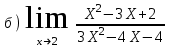 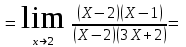 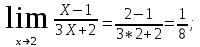 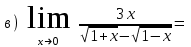 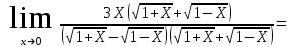 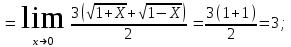 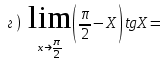 Подстановка: 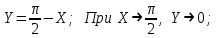 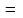 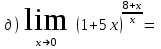 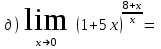 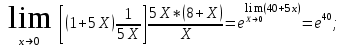 Задание 123. Дана функция y=f(x) и три значения аргумента x1,x2,x3. Установить, является ли эта данная функция непрерывной или разрывной для каждого из данных значений Х. Построить (приближенно) график функции в окрестностях каждой из данных точек. 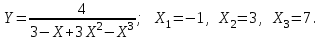 Решение: 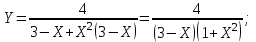 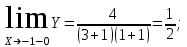 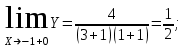 Так как 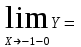 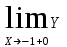 ,то функция в точке Х1=-1 непрерывна. ,то функция в точке Х1=-1 непрерывна.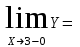 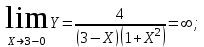 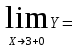 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
