Примерныйвариант экзаменационного (зачетного) билета
1. Вычислить  . Результат изобразить на комплексной плоскости. . Результат изобразить на комплексной плоскости.
2. Доказать, что векторы вида (a, b-a, 2a+b), a,b  R, образуют линейное подпространство в пространстве R, образуют линейное подпространство в пространстве  . Найти его базис и размерность. Дополнить базис подпространства до базиса всего пространства. . Найти его базис и размерность. Дополнить базис подпространства до базиса всего пространства.
3. В пространстве  линейный оператор линейный оператор  – оператор проектирования на ось OZ. Найти матрицу оператора – оператор проектирования на ось OZ. Найти матрицу оператора  в базисе (i, j, k). Найти образ вектора x= 2i – j + 3k. Найти ядро и образ оператора в базисе (i, j, k). Найти образ вектора x= 2i – j + 3k. Найти ядро и образ оператора  . Существует ли обратный оператор? . Существует ли обратный оператор?
4. Квадратичную форму  привести к каноническому виду методом Лагранжа. Найти положительный, отрицательный индексы и ранг формы. Исследовать на знакоопределенность по каноническому виду и по критерию Сильвестра. привести к каноническому виду методом Лагранжа. Найти положительный, отрицательный индексы и ранг формы. Исследовать на знакоопределенность по каноническому виду и по критерию Сильвестра.
5. Матрица Грама в базисе  имеет вид имеет вид  . Найти длины базисных векторов и угол между ними. Ортогонализировать базис . Найти длины базисных векторов и угол между ними. Ортогонализировать базис  . Сделать проверку с помощью матрицы перехода. . Сделать проверку с помощью матрицы перехода.
6. Теоретический вопрос (из списка теоретических вопросов).
7. Разложить многочлен 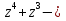 2 2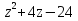 на линейные множители. на линейные множители.
8. В пространстве  многочленов степени не выше 2 оператор многочленов степени не выше 2 оператор  действует по правилу действует по правилу  (p(t)) =t (p(t)) =t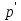 (t)-2p(t-1). Показать линейность оператора. Найти его матрицу в каноническом базисе и в базисе S=( (t)-2p(t-1). Показать линейность оператора. Найти его матрицу в каноническом базисе и в базисе S=( . . |
 Скачать 23.33 Kb.
Скачать 23.33 Kb.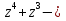 2
2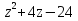 на линейные множители.
на линейные множители. (t)-2p(t-1). Показать линейность оператора. Найти его матрицу в каноническом базисе и в базисе S=(
(t)-2p(t-1). Показать линейность оператора. Найти его матрицу в каноническом базисе и в базисе S=(