математика. Семакин Дмитрий Геннадьевич МАТЕМАТИКА УК-19КЧ ИДО 3Б. Контрольная работа по дисциплине Математика Вариант 8 Исполнитель Семакин Дмитрий Генндьевич группа идо зб ук19 кч
 Скачать 59.81 Kb. Скачать 59.81 Kb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФГБОУ ВПО «Уральский государственный экономический университет» Центр дистанционного образования Контрольная работа по дисциплине: «Математика» Вариант 8 Исполнитель: Семакин Дмитрий Генндьевич группа ИДО ЗБ УК-19 КЧ Екатеринбург 2020 1. Найти матрицу СTАT, если    2. Вычислить определитель  3. Решить систему уравнений с помощью обратной матрицы  Матрица системы Матрица системы  Решить систему уравнений матричным методом Det(A)=1 значит обратная матрица существует Найдём A-1  где Aij-алгебраические дополнения матрицы 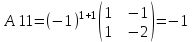 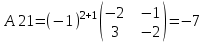  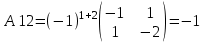   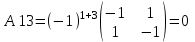  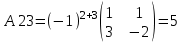  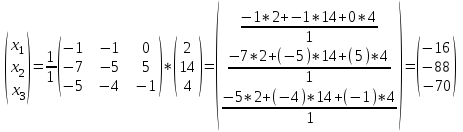 Ответ: x1=-16 x2=-88 x3=-70 4. Решить систему уравнений методом Гаусса  Применяем метод Гаусса для приведения системы к лестничному виду Умножим второе уравнение на (-5) и сложим со вторым уравнением, а результат запишем на место второго уравнения. Умножим второе уравнение на (5) сложим с третьим уравнением, а результат запишем на место третьего уравнения. 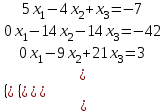 Умножим второе уравнение на (-9) сложим с третьим уравнением, умноженным на (14), а результат запишем на место третьего уравнения.  -420x3=-420 x3=1 -14x2 -14*1=-42 x2=2 5x1-4*2+1=-7 x1=0 Ответ: x1=0, x2=2 x3=0 5. Даны вершины треугольника ABC: A(-4,3) B(7,3) C(1,10) Найти Уравнение прямой АВ Уравнение прямой, проходящей через точки А и B  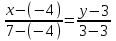 Уравнение стороны AB  Уравнение высоты CH Уравнение перпендикуляра, опущенного из точки C на прямую АВ Из условия перпендикулярности прямых (A1*A2+B1*B2=0) вытекает, что прямые Ax+By+C=0 Bx-Ay+C1=0 перпендикулярны. Уравнение нашей прямой АВ:  перпендикулярна прямая  C1 – найдём из условия, что прямая проходит через точку С(1,10)   Искомая прямая  Уравнение медианы АМ Найдём координаты точки М  Уравнение прямой, проходящей через точки А и М    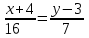 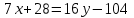  (1;5.18 ) (1;5.18 ) Точку пересечения прямых АМ и СН найдем из решения системы |
