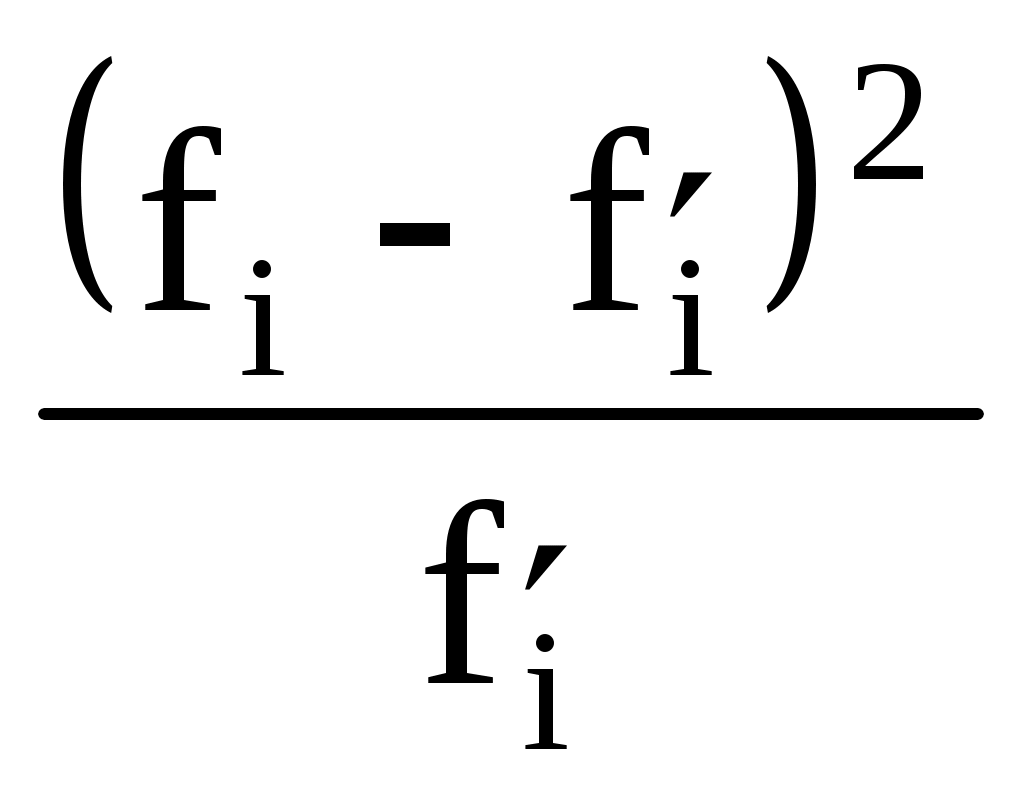В результате эксперимента получены данные, записанные в виде статистического ряда. Требуется

• Название: В результате эксперимента получены данные, записанные в виде статистического ряда. Требуется
• Дата: 10.11.2021
• Размер: 290.5 Kb.
• Имя файла: 10251_17v-IDZ19.1.doc
• Тип: Документы; #267930

ИДЗ 19.1 – Вариант 17.

В результате эксперимента получены данные, записанные в виде статистического ряда. Требуется:

а) записать значения результатов эксперимента в виде вариационного ряда;

б) найти размах варьирования и разбить его на 9 интервалов;

в) построить полигон частот, гистограмму относительных частот и график эмпирической функции распределения;

г) найти числовые характеристики выборки , D_B;

д) приняв в качестве нулевой гипотезу H₀: генеральная совокупность, из которой извлечена выборка, имеет нормальное распределение, проверить ее, пользуясь критерием Пирсона при уровне значимости α = 0,025;

е) найти доверительные интервалы для математического ожидания и среднего квадратичного отклонения при надежности γ = 0,9.

1.17

1,66	2,21	1,21	1,46	1,16	1,81	0,86	1,74	2,08	1,38
2,27	0,81	2,39	2,19	2,25	1,67	1,84	1,37	2,12	2,37
1,15	2,17	1,45	1,75	1,14	1,94	1,53	0,83	1,68	1,35
2,39	1,63	1,86	1,24	1,73	1,07	2,10	1,13	1,91	1,31
1,78	2,09	1,54	1,79	1,08	1,42	0,80	1,96	1,19	0,85
1,88	1,27	0,84	2,60	1,44	1,77	2,45	1,10	2,16	1,59
1,56	2,30	2,48	0,99	1,18	2,11	1,64	2,28	1,29	1,93
2,15	1,72	1,83	1,47	1,87	1,17	2,29	1,90	1,71	2,55
2,31	1,39	1,85	2,38	1,65	2,51	1,48	1,28	2,18	1,49
2,14	1,76	1,51	1,82	0,91	2,51	2,34	2,59	1,69	2,13

Решение:

а) Располагаем значения результатов эксперимента в порядке возрастания, т.е. записываем вариационный ряд:

0,8	0,81	0,83	0,84	0,85	0,86	0,91	0,99	1,07	1,08
1,1	1,13	1,14	1,15	1,16	1,17	1,18	1,19	1,21	1,24
1,27	1,28	1,29	1,31	1,35	1,37	1,38	1,39	1,42	1,44
1,45	1,46	1,47	1,48	1,49	1,51	1,53	1,54	1,56	1,59
1,63	1,64	1,65	1,66	1,67	1,68	1,69	1,71	1,72	1,73
1,74	1,75	1,76	1,77	1,78	1,79	1,81	1,82	1,83	1,84
1,85	1,86	1,87	1,88	1,9	1,91	1,93	1,94	1,96	2,08
2,09	2,1	2,11	2,12	2,13	2,14	2,15	2,16	2,17	2,18
2,19	2,21	2,25	2,27	2,28	2,29	2,3	2,31	2,34	2,37
2,38	2,39	2,39	2,45	2,48	2,51	2,51	2,55	2,59	2,6

б) По статистическим данным находим:

Находим размах варьирования:

Составим интервальный статистический ряд распределения случайной величины, разбив размах варьирования на l = 9 интервалов.

По формуле вычисляем длину частотного интервала



В качестве границы первого интервала можно выбрать значение x_min. (Например у нас x_min = 0,8)

Тогда границы следующих частичных интервалов вычисляем по формуле

Первый интервал [0,8; 0,8+0,2] = [0,8; 1,0]

Второй интервал [1,0; 1,0+0,2] = [1,0; 1,2]

Третий интервал [1,2; 1,2+0,2] = [1,2; 1,4]

Четвертый интервал [1,4; 1,4+0,2] = [1,4; 1,6] и т.д.

Находим середины интервалов:

Подсчитываем число значений результатов эксперимента, попавших в каждый интервал, т.е. находим частоты интервалов f_i.

Далее вычисляем относительные частоты , где n = 100

И их плотности

Полученные результаты помещаем в таблицу

Номер частичного интервала li	Границы интервала		Середина интервала	Частота интервала fi	Относительная частота	Плотность относительной частоты	Накопленная частота
	xi	xi+1
1	0,8	1,0	0,9	8	0,08	0,4	0,08
2	1,0	1,2	1,1	10	0,10	0,5	0,18
3	1,2	1,4	1,3	10	0,10	0,5	0,28
4	1,4	1,6	1,5	12	0,12	0,6	0,40
5	1,6	1,8	1,7	16	0,16	0,8	0,56
6	1,8	2,0	1,9	13	0,13	0,65	0,69
7	2,0	2,2	2,1	12	0,12	0,6	0,81
8	2,2	2,4	2,3	12	0,12	0,6	0,93
9	2,4	2,6	2,5	7	0,07	0,35	1
	−	−	−	100	−	−	−

в) Построим полигон частот

По горизонтальной оси отложим середины интервалов, а по вертикальной – частоты интервалов.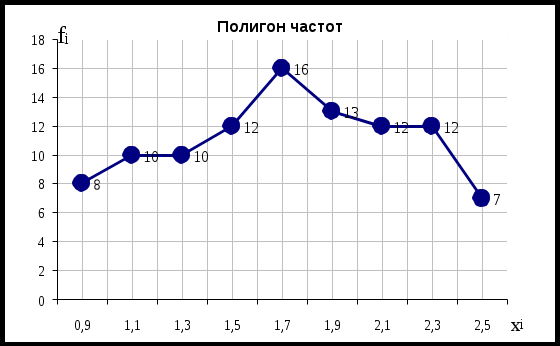



Построим гистограмму относительных частот:

По горизонтальной оси отложим интервалы изменения признака, а по вертикальной – относительные частоты интервала.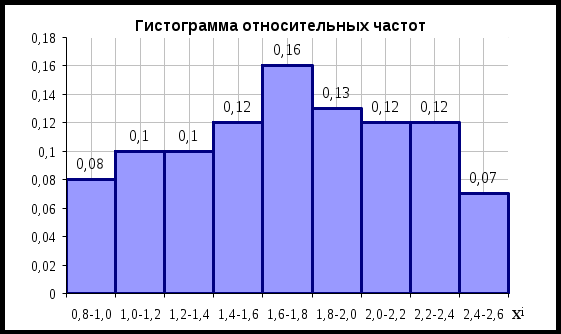


Находим значения эмпирической функции распределения


Построим эмпирическую функцию распределения: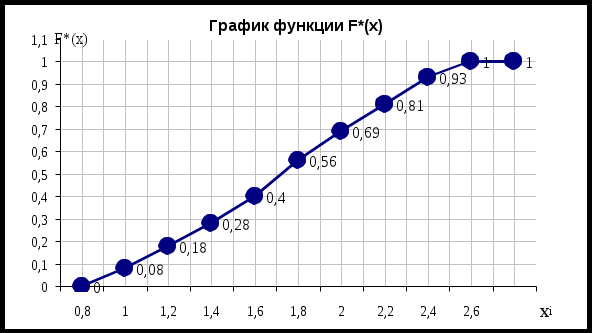




г) найти числовые характеристики выборки , D_B;

Для этого составляем расчетную таблицу, из нее получаем:

mi	Границы интервала		Середина интервала	Частота интервала fi
	xi	xi+1
1	0,8	1,0	0,9	8	7,2	0,81	6,48
2	1,0	1,2	1,1	10	11	1,21	12,1
3	1,2	1,4	1,3	10	13	1,69	16,9
4	1,4	1,6	1,5	12	18	2,25	27
5	1,6	1,8	1,7	16	27,2	2,89	46,24
6	1,8	2,0	1,9	13	24,7	3,61	46,93
7	2,0	2,2	2,1	12	25,2	4,41	52,92
8	2,2	2,4	2,3	12	27,6	5,29	63,48
9	2,4	2,6	2,5	7	17,5	6,25	43,75
	−	−	−	100	171,4	−	315,8

Найдем выборочную среднюю, выборочную дисперсию и выборочное среднее квадратическое отклонение. Выборочную среднюю найдем по формуле:





где n - количество интервалов, x´_i – середина интервала.

Выборочную дисперсию найдем по формуле:





Выборочная дисперсия является смещенной оценкой генеральной дисперсии, а исправленная дисперсия – несмещенной оценкой:

;

д) приняв в качестве нулевой гипотезу H₀: генеральная совокупность, из которой извлечена выборка, имеет нормальное распределение, проверить ее, пользуясь критерием Пирсона при уровне значимости α = 0,025;

Согласно критерию Пирсона необходимо сравнить эмпирические и теоретические частоты. Эмпирические частоты даны. Найдём теоретические частоты. Для этого пронумеруем Х, т.е. перейдём к случайной величине и вычислим концы интервалов: , причём наименьшее значение z, точнее z₁ положим стремящимся к −∞, а наибольшее, точнее z_i+1 - стремящемся к +∞.

Строим расчётную таблицу:

i	Границы интервала				Границы интервала (zi, zi+1)
	xi	xi+1
1	0,8	1,0	−	−0,714	−	−1,51
2	1,0	1,2	−0,714	−0,514	−1,51	−1,09
3	1,2	1,4	−0,514	−0,314	−1,09	−0,67
4	1,4	1,6	−0,314	−0,114	−0,67	−0,24
5	1,6	1,8	−0,114	0,086	−0,24	0,18
6	1,8	2,0	0,086	0,286	0,18	0,61
7	2,0	2,2	0,286	0,486	0,61	1,03
8	2,2	2,4	0,486	0,686	1,03	1,45
9	2,4	2,6	0,686	−	1,45	−

Находим теоретические вероятности P_i и теоретические частоты: .

Значения Ф(z_i) и Ф(z_i+1) находим по таблице Лапласа.

Составляем расчётную таблицу.

i	Границы интервала		Ф(zi)	Ф(zi+1)	Pi = Ф(zi+1)−Ф(zi)	f'i = 100Pi
	zi	zi+1
1	−	−1,51	−0,5000	−0,4345	0,0655	6,55
2	−1,51	−1,09	−0,4345	−0,3621	0,0724	7,24
3	−1,09	−0,67	−0,3621	−0,2486	0,1135	11,35
4	−0,67	−0,24	−0,2486	−0,0948	0,1538	15,38
5	−0,24	0,18	−0,0948	0,0714	0,1662	16,62
6	0,18	0,61	0,0714	0,2291	0,1577	15,77
7	0,61	1,03	0,2291	0,3485	0,1194	11,94
8	1,03	1,45	0,3485	0,4265	0,078	7,8
9	1,45	−	0,4265	0,5000	0,0735	7,35
	−	−	−	−	1	100

Вычислим наблюдаемое значение критерия Пирсона.

Для этого составляем расчётную таблицу.

Последние два столбца служат для контроля вычислений по формуле:

i	fi	f´i	fi − f´i
1	8	6,55	1,45	0,321	64	9,771
2	10	7,24	2,76	1,0522	100	13,8122
3	10	11,35	−1,35	0,1606	100	8,8106
4	12	15,38	−3,38	0,7428	144	9,3628
5	16	16,62	−0,62	0,0231	256	15,4031
6	13	15,77	−2,77	0,4866	169	10,7166
7	12	11,94	0,06	0,0003	144	12,0603
8	12	7,8	4,2	2,2615	144	18,4615
9	7	7,35	−0,35	0,0167	49	6,6667
	100	100	−		−	105,0648

Контроль: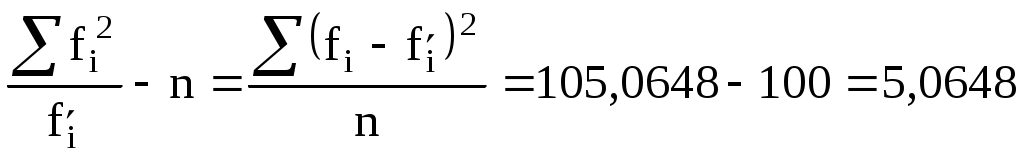

По таблице критических значений при уровне значимости α = 0,025 и числе степеней

свободы k = l – s – 1 = 9 – 2 – 1 = 6 найдем

Так как

Таким образом , то есть на уровне значимости α = 0,025 принимаем нулевую гипотезу H₀ о том, что генеральная совокупность, из которой извлечена выборка имеет нормальное распределение.
е) найти доверительные интервалы для математического ожидания и среднего квадратичного отклонения при надежности γ = 0,9.

= 1,714, n = 100, σ_В = 0,4716.

Если случайная величина (СВ) X генеральной совокупности распределена нормально, то с надежностью γ можно утверждать, что математическое ожидание M(X) СВ X покрывается доверительным интервалом





По таблице функции Лапласа приложения 4 находим



Получим


Доверительный интервал для среднего квадратического отклонения при большом объеме выборки n > 30, определяется выражением



Ввиду достаточно большого количества наблюдений смещенностью найденного значения σ пренебрегаем.

Таким образом, искомый доверительный интервал: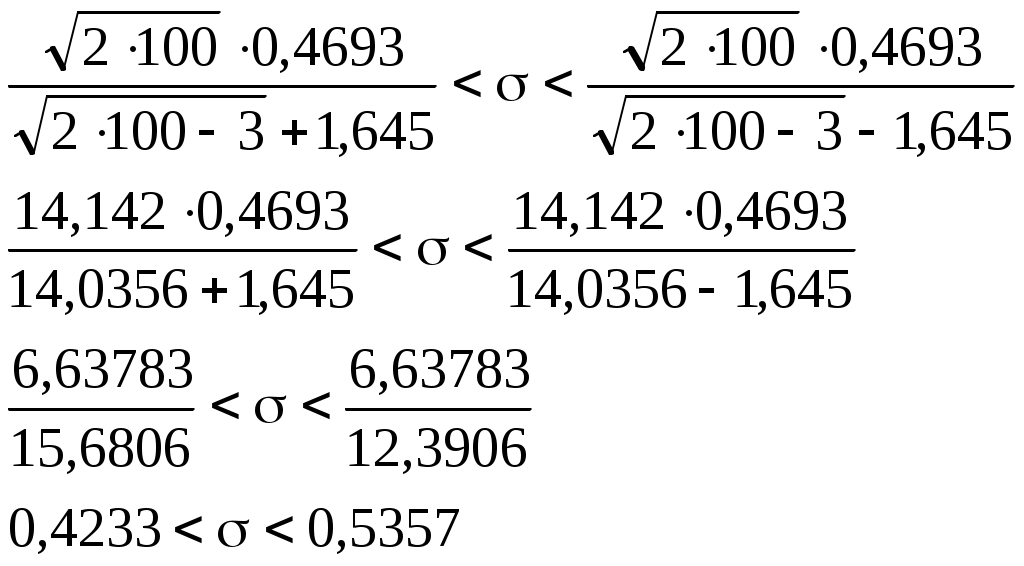