Математическая статистика в психологии. Волгоград.(9 задач).. Решение 1) Представим данные в табличной форме. Запишем в таблицу частоты, частости (в долях единицы и в процентах), накопленные частоты, накопленные частости

Название	Решение 1) Представим данные в табличной форме. Запишем в таблицу частоты, частости (в долях единицы и в процентах), накопленные частоты, накопленные частости
Дата	22.02.2023
Размер	0.6 Mb.
Формат файла
Имя файла	Математическая статистика в психологии. Волгоград.(9 задач)..doc
Тип	Задача #950196
страница	1 из 3

1 2 3

Задача №1
Изучалась стрессоустойчивость у учащихся 10-11 классов. В исследовании принимали 50 человек. Были получены следующие результаты:

133; 132; 134; 134; 135; 128; 125; 126; 124; 129; 123; 125; 122; 127; 129; 125; 127; 130; 136; 136; 130; 123; 125; 125; 128; 129; 126; 133; 131; 124; 125; 129; 126; 131; 130; 133; 128; 126; 133; 132; 129; 131; 130; 127; 129; 128; 132; 133; 135; 128.

Представить данные в табличной форме. Построить таблицы частот, частостей (в долях единицы и в процентах), накопленных частот, накопленных частостей.

Представить данные в графическом виде: полигон частот, кривая распределения, диаграмма, кумулята.
Решение:
1) Представим данные в табличной форме. Запишем в таблицу частоты, частости (в долях единицы и в процентах), накопленные частоты, накопленные частости.

Результаты расчетов представим в табл. 1.1.

Таблица 1.1

Распределение учащихся 10-11 классов по стрессоустойчивости

Стрессоустой-чивость, балл	Число учащихся, чел.	Частость		Накопленные частоты, чел.	Накопленные частости
Стрессоустой-чивость, балл	Число учащихся, чел.	в долях	в %	Накопленные частоты, чел.	Накопленные частости
1	2	3	4	5	6
122	1	0,02	2	1	0,02
123	2	0,04	4	3	0,06

Таблица 1.1 (продолжение)

1	2	3	4	5	6
124	2	0,04	4	5	0,10
125	6	0,12	12	11	0,22
126	4	0,08	8	15	0,30
127	3	0,06	6	18	0,36
128	5	0,10	10	23	0,46
129	6	0,12	12	29	0,58
130	4	0,08	8	33	0,66
131	3	0,06	6	36	0,72
132	3	0,06	6	39	0,78
133	5	0,10	10	44	0,88
134	2	0,04	4	46	0,92
135	2	0,04	4	48	0,96
136	2	0,04	4	50	1,00
	50	1,00	100	–	–

2) Представить данные в графическом виде.

а) эмпирическая функция распределения.

б) полигон частот.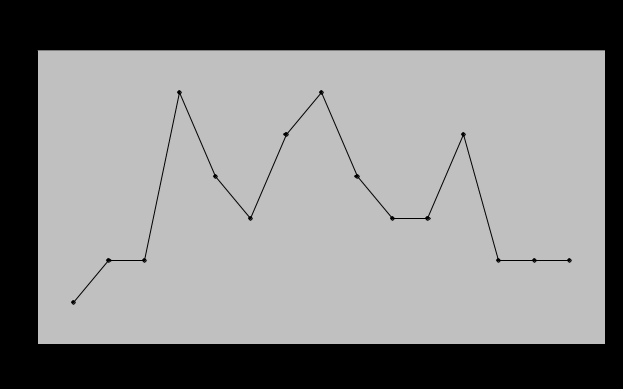

в) кумулята распределения.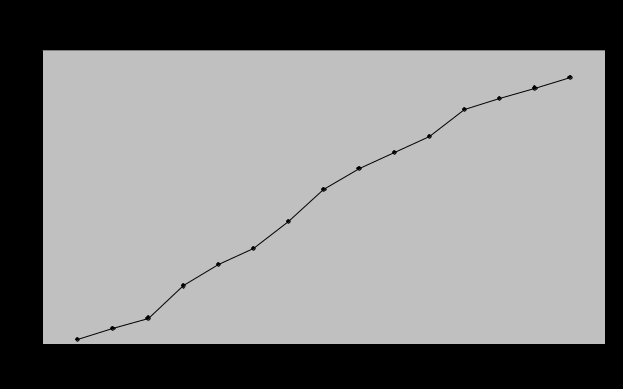

Задача №2
При проведении тестового задания студентами были получены следующие результаты (в баллах):

139, 180, 131, 145, 169, 172, 158, 162, 156, 174, 166, 170, 170, 195, 178, 153, 138, 130, 142, 155, 164, 187, 180, 161, 166, 177, 145, 158, 157, 148, 171, 128, 135, 148, 127, 146, 158, 169, 159, 166, 160, 147, 179, 176, 168, 124, 188, 192, 166, 137.

Представить данные в табличной форме, при этом группировать данные так, чтобы получилось 8 разрядов. Построить таблицу частот, частостей, накопленных частот, накопленных частостей.
Решение:
Проведем группировку студентов по результатам проведения тестового задания, образовав 8 групп с равными интервалами.

Определим длину интервала.

баллов

Таблица 2.1

Распределение студентов по результатам тестового задания

Группы по результатам, балл	Число студентов, чел.	Частость	Накопленные частоты, чел.	Накопленные частости
1	2	3	4	5
124,0 – 132,9	5	0,10	5	0,10
132,9 – 141,8	4	0,08	9	0,18

Таблица 2.1 (продолжение)

1	2	3	4	5
141,8 – 150,7	7	0,14	16	0,32
150,7 – 159,6	8	0,16	24	0,48
159,6 – 168,5	9	0,18	33	0,66
168,5 – 177,4	9	0,18	42	0,84
177,4 – 186,3	4	0,08	46	0,92
186,3 – 195,0	4	0,08	50	1,00
	50	1,00	–	–

Запишем в табл. 2.1 частоты, частости, накопленные частоты, накопленные частости.

Задача №3
При проведении исследования индивидуальных особенностей памяти были получены следующие результаты (в баллах):

18; 17; 16; 15; 14; 13; 17; 13; 14; 15; 16; 17; 12; 17; 16; 15; 14; 15; 12: 12; 14; 15; 17; 17; 11; 15; 14; 13; 18; 15; 12; 13; 19; 15; 14; 13; 14; 11; 17; 13; 14; 15; 16; 17; 13; 19; 18; 17; 17; 16; 11; 14; 15; 11; 12; 13; 14; 15; 16; 17; 18; 19; 13; 19; 16; 12; 14; 16; 15; 16; 15; 16; 17; 16; 15; 14; 13; 14; 15; 16; 17; 16; 18; 19; 18; 11; 16; 15; 16; 13; 18; 17; 15; 14; 13; 18; 15; 19; 17; 16.

Посчитать среднее арифметическое полученных результатов, определить моду, медиану, посчитать размах данных, дисперсию, стандартное отклонение.
Решение:
1) Составим дискретный вариационный ряд.

Таблица 3.1

Распределение по индивидуальным особенностям памяти

Индивидуальные особенности памяти, балл	Число опытов	Накопленные частоты
1	2	3
11	5	5
12	6	11
13	12	23
14	14	37
15	18	55
16	16	71
17	15	86

Таблица 3.1 (продолжение)

1	2	3
18	8	94
19	6	100
	100	–

2) Определим:

а) среднее арифметическое.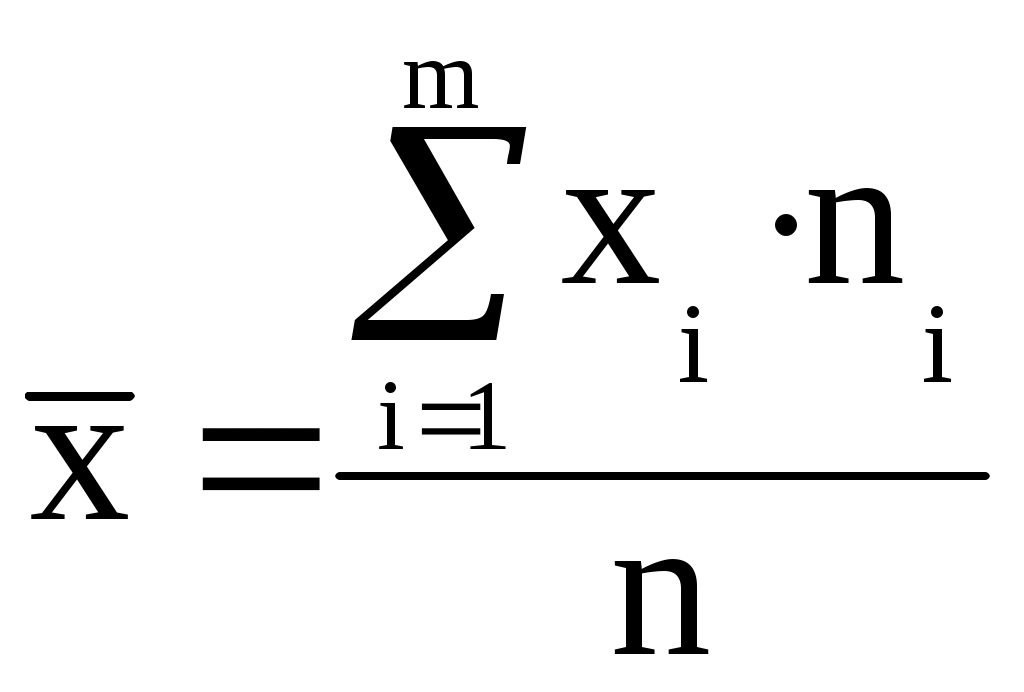

Промежуточные расчеты представим в табл. 3.2.

Таблица 3.2


1	2	3	4	5	6
11	5	55	-4,18	17,4724	87,3620
12	6	72	-3,18	10,1124	60,6744
13	12	156	-2,18	4,7524	57,0288
14	14	196	-1,18	1,3924	19,4936
15	18	270	-0,18	0,0324	0,5832
16	16	256	0,82	0,6724	10,7584
17	15	255	1,82	3,3124	49,6860
18	8	144	2,82	7,9524	63,6192
19	6	114	3,82	14,5924	87,5544
	100	1518	–	–	436,7600

балла

Таким образом, средний балл индивидуальных особенностей памяти при проведении исследования составит 15,18 балла.

б) моду.

Мо = 15 баллов

Таким образом, в исследуемой совокупности преобладают опыты, в которых индивидуальные особенности памяти составили 15 баллов.

в) медиану.

Ме = 15 баллов

Таким образом, в исследуемой совокупности в 50% опытах, индивидуальные особенности памяти составили менее 15 баллов, а в 50% опытах – более 15 баллов.

г) размах.

R = 19 – 11 = 8 баллов

Индивидуальные особенности памяти в исследуемой совокупности колеблются от 11 до 19 баллов.

д) дисперсию и среднее квадратическое отклонение.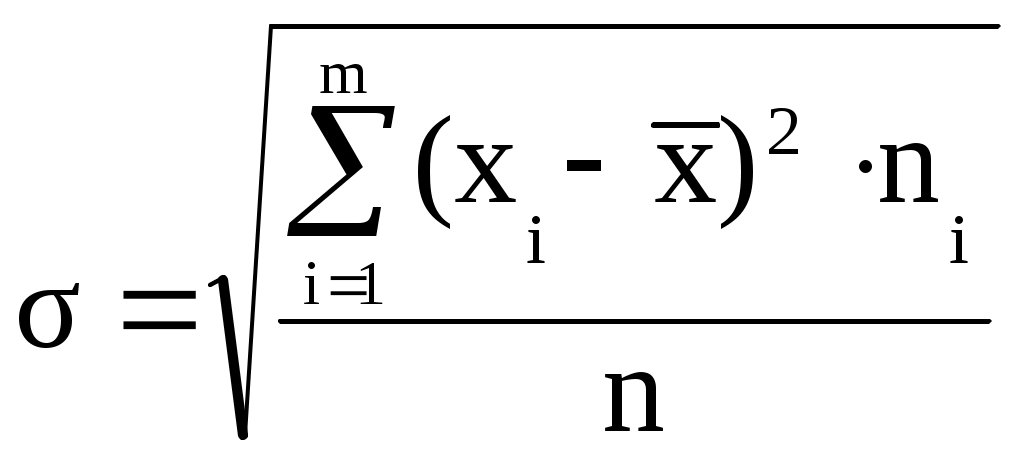

= 2,09 балла

= 4,3676

1 2 3