Главная страница
Навигация по странице:

  • Список литературы

    		•

    Математическая статистика в психологии. Волгоград.(9 задач).. Решение 1) Представим данные в табличной форме. Запишем в таблицу частоты, частости (в долях единицы и в процентах), накопленные частоты, накопленные частости


    Скачать 0.6 Mb.
    НазваниеРешение 1) Представим данные в табличной форме. Запишем в таблицу частоты, частости (в долях единицы и в процентах), накопленные частоты, накопленные частости
    Дата22.02.2023
    Размер0.6 Mb.
    Формат файлаdoc
    Имя файлаМатематическая статистика в психологии. Волгоград.(9 задач)..doc
    ТипЗадача
    #950196
    страница3 из 3
    1   2   3

    Задача №10
        В начале и в конце учебного года проводилось изучение мотивационной сферы  студентов. Полученные результаты приведены в таблице:

    номер испытуемого
    1
    2
    3
    4
    5
    6
    7
    8
    9

    начало уч.г.
    37
    23
    36
    19
    24
    23
    21
    31
    22

    конец уч.г.
    28
    28
    34
    23
    29
    30
    28
    28
    28


    С помощью Т-критерия Вилкоксона определить, являются ли изменения в эмоциональной сфере студентов в течение года статистически достоверными.
    Решение:
    С помощью Т-критерия Вилкоксона определим, являются ли изменения в эмоциональной сфере студентов в течение года статистически достоверными.

    : преобладание положительного сдвига в эмоциональной сфере студентов является случайным.

    : преобладание положительного сдвига в эмоциональной сфере студентов не является случайным.

    Запишем значения в таблицу (табл. 10.1).

    Таблица 10,1

    № испытуемого
    начало у.г.
    конец у.г.
    разность (после-до)
    значение разности по модулю
    ранг разности

    1
    2
    3
    4
    5
    6

    1
    37
    28
    -9
    9
    9

    2
    23
    28
    5
    5
    4,5

    3
    36
    34
    -2
    2
    1

    Таблица 10.1 (продолжение)

    1
    2
    3
    4
    5
    6

    4
    19
    23
    4
    4
    3

    5
    24
    29
    5
    5
    4,5

    6
    23
    30
    7
    7
    7,5

    7
    21
    28
    7
    7
    7,5

    8
    31
    28
    -3
    3
    2

    9
    22
    28
    6
    6
    6


    Рассчитаем разность значений. Для данного случая типичным сдвигом будет считаться сдвиг в положительную сторону, а не типичным сдвиг в отрицательную сторону.

    Найдем Т эмпирическое вычислив сумму рангов в нетипичном направлении.

    Т = 9 + 1 + 2 = 12

    Критические значения: , .

    Так как Т > , T > то отвергаем. Другими словами, изменения в эмоциональной сфере студентов в течение года являются статистически недостоверными.

    Задача №15
    Девять испытуемых (А, Б, В и т.д.) в экспериментах по запоминанию в ситуациях с помехами и без них  имели следующие результаты (в баллах):

    испытуемый
    А
    Б
    В
    Г
    Д
    Е
    Ж
    З
    И

    без помех
    6
    7
    6
    8
    7
    6
    5
    6
    4

    с помехами
    3
    4
    5
    6
    6
    5
    4
    5
    2


    Определить, используя коэффициент корреляции Пирсона, существует ли значимая корреляционная связь между показателями. При этом считать, что оба распределения являются нормальными.
    Решение:
    Определим коэффициент корреляции Пирсона.



    Промежуточные расчеты представим в табл. 15.1.

    Таблица 15.1

    № п/п










    1
    2
    3
    4
    5
    6

    1
    6
    3
    36
    18
    9

    2
    7
    4
    49
    28
    16

    3
    6
    5
    36
    30
    25

    4
    8
    6
    64
    48
    36

    5
    7
    6
    49
    42
    36

    6
    6
    5
    36
    30
    25

    7
    5
    4
    25
    20
    16



    Таблица 15.1 (продолжение)

    1
    2
    3
    4
    5
    6

    8
    6
    5
    36
    30
    25

    9
    4
    2
    16
    8
    4



    55
    40
    347
    254
    192

    Средняя
    6,11
    4,44
    38,56
    28,22
    21,33




    Оценим значимость вычисленного коэффициента.

    : = 0.

    : ≠ 0.

    Критические значения:

    = 0,67 для р ≤ 0,05, = 0,80 для р ≤ 0,01

    Так как > , отвергаем. Другими словами, на 5%-ом уровне значимости между результатами экспериментов по запоминанию в ситуациях с помехами и без помех присутствует прямая и тесная связь. (0,05 < р < 0,01).

    Задача №17
    Проводится исследование формирования моторного навыка. Записать уравнение регрессии для «независимой переменной» Х и «зависимой переменной» Y. В качестве переменной Х выступает номер пробы,

    Y – количество верно выполненных заданий (берется среднее арифметическое значений для группы испытуемых). Полученные результаты:

    № пробы


    1
    2
    3
    4
    5
    6
    7

    кол-во заданий


    14
    15
    18
    20
    20
    21
    23


    Решение:
    Построим уравнение парной регрессии зависимости Y от Х.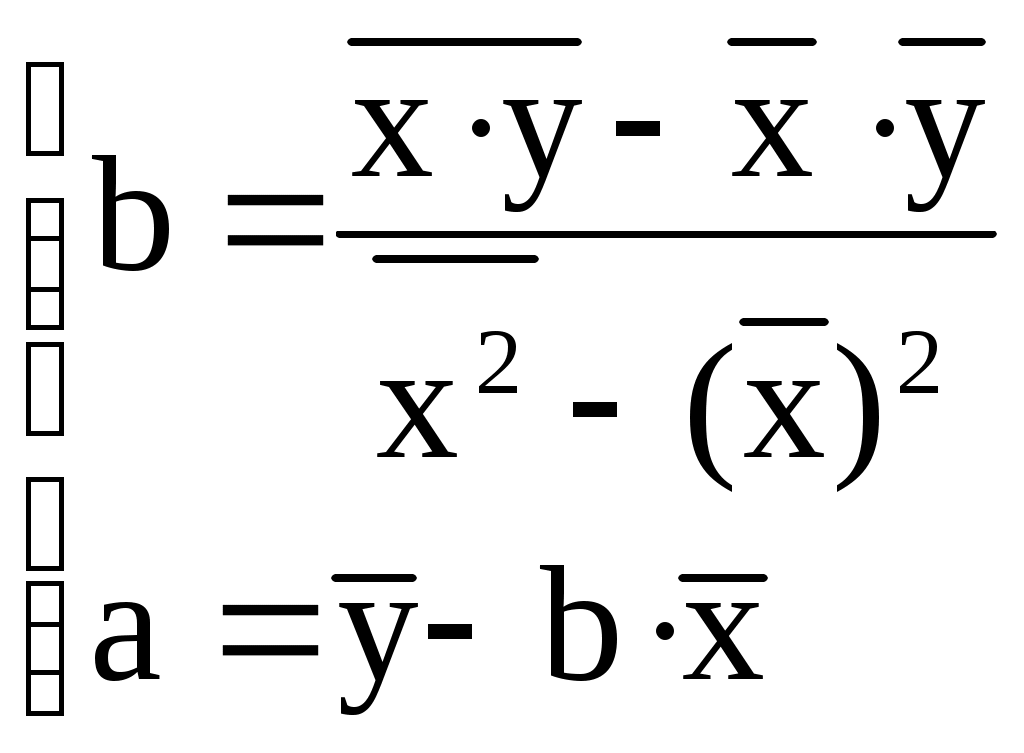

    = a + b∙x, где



    Промежуточные расчеты представим в табл. 17.1.

    Таблица 17.1

    № п/п










    1
    2
    3
    4
    5
    6

    1
    1
    14
    1
    14
    14,3

    2
    2
    15
    4
    30
    15,8

    3
    3
    18
    9
    54
    17,3

    4
    4
    20
    16
    80
    18,7



    Таблица 17.1 (продолжение)

    1
    2
    3
    4
    5
    6

    5
    5
    20
    25
    100
    20,2

    6
    6
    21
    36
    126
    21,6

    7
    7
    23
    49
    161
    23,1



    28
    131
    140
    565
    131

    Средняя
    4
    18,71
    20
    80,71
    –




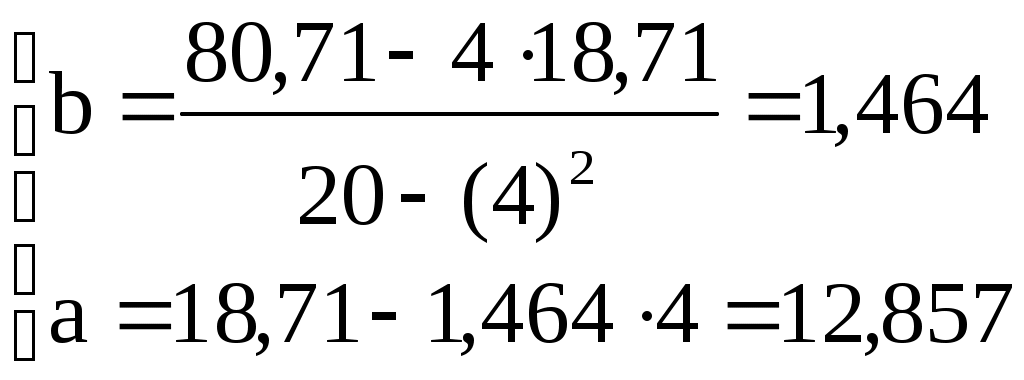    Отсюда уравнение имеет вид:

    = 12,857 + 1,464х

    С увеличением номера пробы на 1 количество верно выполненных заданий увеличится на 1,464.


    Список литературы
    1. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: Учеб. пособие для студентов вузов. Изд. 5-е, стер. – М.: Высш. шк., 2001. – 400с.

    2. Математические методы в психологии и педагогике: учебное пособие /

    О.Г. Берестнева, Е.А. Муратова, И. Л. Шелехов, О.С. Жаркова, А.М.

    Уразаев. – Томск: Издательство Томского государственного педагогического

    университета, 2011. – 282с.



    1   2   3

    написать администратору сайта