Технологии статистических расчетов в MS EXCEL. Лабораторная_работа_25. Лабораторная работа 25. Технологии статистических расчетов в ms excel
 Скачать 249 Kb.
|
Лабораторная работа №25. Технологии статистических расчетов в MS EXCEL.Цель: научиться использовать возможности MS Excel для проведения статистических расчетов. Задачи: Расчет коэффициента корреляции Пирсона и t-статистики Стьюдента. Построение модели регрессии различными способами. Выбор наиболее точной модели связи между двумя величинами. 1. Параметрический корреляционный анализ.Одна из наиболее распространенных задач статистического исследования состоит в изучении связи между выборками. Обычно связь между выборками носит не функциональный, а вероятностный (или стохастический) характер. В этом случае нет строгой, однозначной зависимости между величинами. При изучении стохастических зависимостей различают корреляцию и регрессию. Корреляционный анализ состоит в определении степени связи между двумя случайными величинами Xи Y. В качестве меры такой связи используется коэффициент корреляции. Коэффициент корреляции оценивается по выборке объема п связанных пар наблюдений (xi, yi) из совместной генеральной совокупности Xи Y. Существует несколько типов коэффициентов корреляции, применение которых зависит от измерения (способа шкалирования) величин Xи Y. Для оценки степени взаимосвязи величин Xи Y, измеренных в количественных шкалах, используется коэффициент линейной корреляции (коэффициент Пирсона), предполагающий, что выборки Xи Y распределены по нормальному закону. 1. Линейный коэффициент корреляции — параметр, который характеризует степень линейной взаимосвязи между двумя выборками, рассчитывается по формуле: 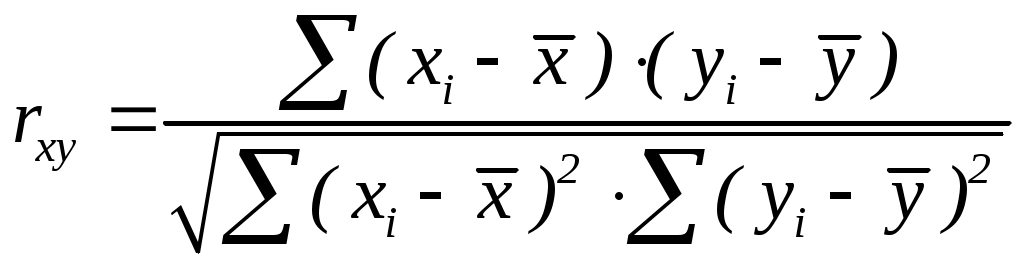 где хi — значения, принимаемые в выборке X, yi — значения, принимаемые в выборке Y;  — средняя по X,  — средняя по Y. Коэффициент корреляции изменяется от -1 до 1. Когда при расчете получается величина большая +1 или меньшая -1 — следовательно, произошла ошибка в вычислениях. При значении 0 линейной зависимости между двумя выборками нет. Знак коэффициента корреляции очень важен для интерпретации полученной связи. Если знак коэффициента линейной корреляции — плюс, то связь между коррелирующими признаками такова, что большей величине одного признака (переменной) соответствует большая величина другого признака (другой переменной). Иными словами, если один показатель (переменная) увеличивается, то соответственно увеличивается и другой показатель (переменная). Такая зависимость носит название прямо пропорциональной зависимости. Если же получен знак минус, то большей величине одного признака соответствует меньшая величина другого. Иначе говоря, при наличии знака минус, увеличению одной переменной (признака, значения) соответствует уменьшение другой переменной. Такая зависимость носит название обратно пропорциональной зависимости. Теснота связи и величина коэффициента корреляции.
2. t-статистика Стьюдента.Для того чтобы оценить наличие связи между двумя переменными, также можно использовать t-статистику Стьюдента, которая оценивает отношение величины линейного коэффициента корреляции к среднему квадратическому отклонению и рассчитывается по формуле 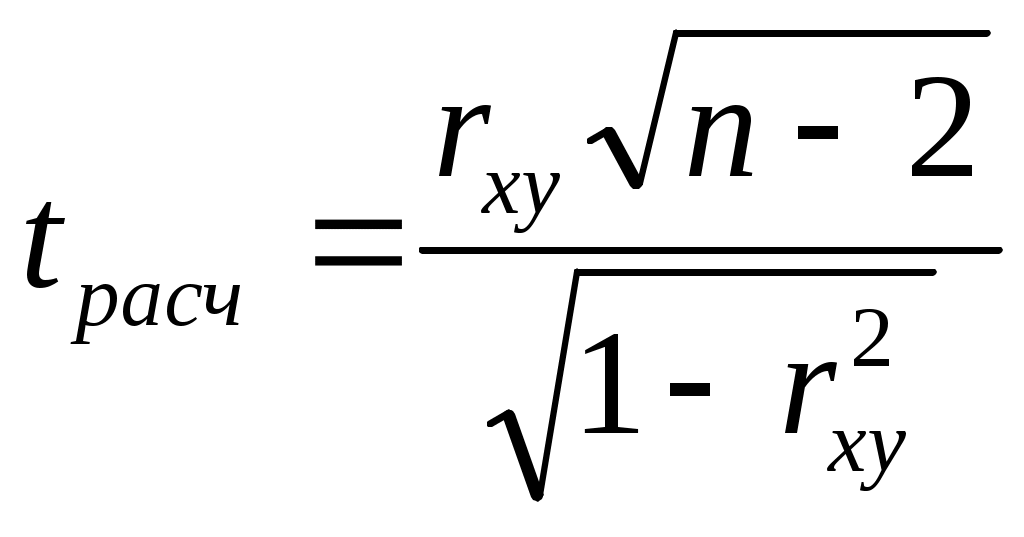 Полученную величину tрасч сравнивают с табличным значением t-критерия Стьюдента с n-2 степенями свободы. Если tрасч > tтабл, то практически невероятно, что найденное значение обусловлено только случайными совпадениями величин X и Y d в выборке из генеральной совокупности, т.е. существует зависимость между X и Y. И наоборот, если tрасч < tтабл , то величины X и Y независимы. 3. Регрессионный анализ.Цель регрессионного анализа – определить количественные связи между зависимыми случайными величинами. Одна из этих величин полагается зависимой и называется откликом, другие – независимые, называются факторами. Для установления степени зависимости между откликом и факторами используются вычисляемые величины ковариации и коэффициент корреляции. Если коэффициент корреляции по абсолютной величине близок к единице, то для построения зависимости используется линейная модель. Для других случаев используются более сложные нелинейные модели. Уравнение линейной регрессии имеет вид: Y=a1X1 + a2X2 + …+ akXk, где а1, а2… аk – параметры, подлежащие определению методом наименьших квадратов (МНК). В среде MS Excel для этого используется встроенная функция ЛИНЕЙН и инструмент Регрессия из Пакета анализа. Задание 1. Исследование связей между двумя исследуемыми признаками. Условие задачи: По 20 туристическим фирмам были установлены затраты на рекламную кампанию и количество туристов, воспользовавшихся после ее проведения услугами каждой фирмы. Определить коэффициент корреляции между исследуемыми признаками. Ход выполнения: Откройте новую книгу MS Excel и создайте таблицу согласно рис. 1: 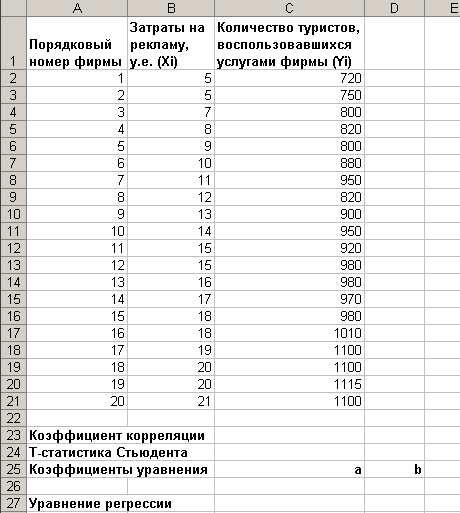 Рис.1. Рассчитайте в ячейке С23 коэффициент корреляции, используя функцию КОРРЕЛ из категории Статистические. Синтаксис функции: КОРРЕЛ (массив1 ; массив 2): где массив1 – ссылка на диапазон ячеек первой выборки (X); массив2 – ссылка на диапазон ячеек второй выборки (Y). В нашей задаче формула будет иметь вид: =КОРРЕЛ(B2:B21;C2:C21) Сделайте вывод о тесноте связи между затратами на рекламу и количеством привлеченных туристов.  Оцените значимость коэффициента корреляции. С этой целью рассматриваются две гипотезы. Основная Н0: xy=0 и альтернативная Н1: xy≠0. Для проверки гипотезы Н0 рассчитайте t-статистику Стьюдента по формуле, указанной выше в ячейке С24. В нашем случае число степеней свободы ν = n-2=20-2 = 18 и формула будет следующей: =C23*КОРЕНЬ(20-2)/КОРЕНЬ(1-(C23*C23)) Сравните полученное значение с критическим значением tν,α распределения Стьюдента. (При ν =18 и доверительной вероятности α = 0,05, tν,α,табл = 1,734). Сделайте вывод о наличии связи между исследуемыми величинами.  Задание 2. Построение регрессионной модели. 1-й способ. Функция ЛИНЕЙН. В первом способе для получения коэффициентов а и b линейного уравнения регрессии Y=а*X+b, описывающего зависимость количества привлеченных туристов от затрат на рекламу воспользуемся статистической функцией ЛИНЕЙН. Для этого выделите две ячейки C26:D26 и выполните вставку функции ЛИНЕЙН с аргументами согласно рис.2. Здесь Известные_значения_y – диапазон значений Количество туристов, Известные_значения_x – диапазон значений Затраты на рекламу. Нажмите комбинацию клавиш SHIFT+CTRL+ENTER. 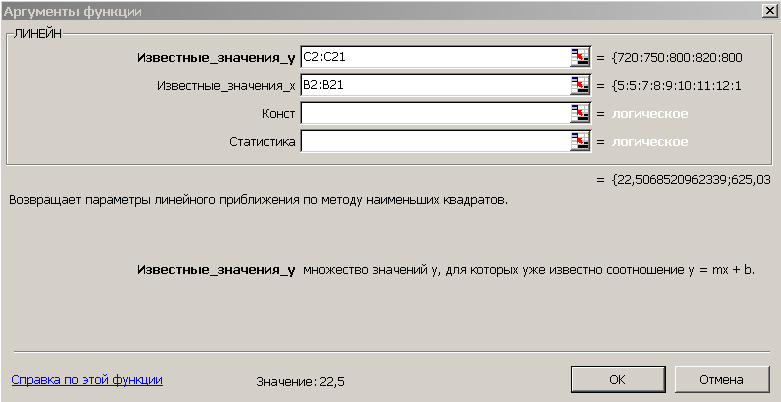 Рис. 2. Аргументы функции ЛИНЕЙН. В ячейку D27 введите уравнение Y= a*X+b (вместо a и b подставьте полученные коэффициенты линейной регрессии).  2-й способ (графический). Построение линии тренда. Для получения уравнения регрессии построим корреляционное поле переменных X (затраты на рекламу) и Y (количество туристов). Выделите диапазон ячеек В2:С21, запустите мастера диаграмм и выберите тип диаграммы – Точечная. Задайте для диаграммы имя – Корреляционное поле, ось Х – Затраты на рекламу, ось Y – Количество туристов. На последнем шаге мастера укажите место расположения – отдельный лист. Добавьте линию тренда на точечный график. Для этого необходимо выделить диаграмму и выполнить команду меню Диаграмма /Добавить линию тренда, либо выполнить данную команду из контекстного меню, щелкнув по любой точке графика. Линия тренда – графическое представление направления изменения ряда данных Выберите тип тренда Линейный, который используется для аппроксимации данных по методу наименьших квадратов в соответствии с уравнением: y = ax +b, где a — угол наклона и b — координата пересечения оси абсцисс. На вкладке Параметры установите флажки Показать уравнение на диаграмме и Поместить на диаграмму величину достоверности аппроксимации  . Щелкните по кнопке ОК. - это число от 0 до 1, которое отражает близость линии тренда к фактическим данным. Линия тренда наиболее соответствует действительности, когда значение близко к 1. Сравните уравнение регрессии, полученное графическим методом (рис. 3), с уравнением, рассчитанным с помощью функции ЛИНЕЙН. 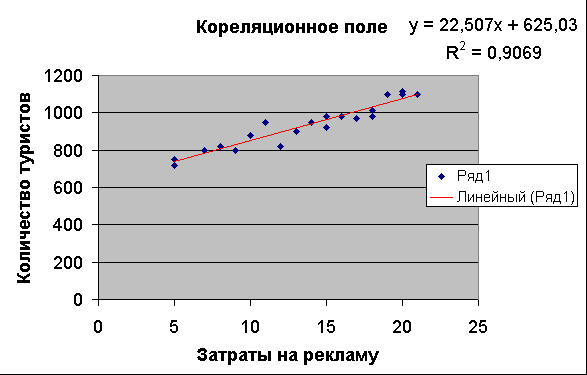 Рис.3. 3-й способ. Инструмент анализа Регрессия. Сначала убедитесь, что был активизирован Пакет анализа, т.е. в меню Сервис есть команда Анализ данных. Если нет, то выполните команду Сервис/Надстройки. В диалоговом окне Надстройки установите флажок Пакет анализа и щелкните по кнопке ОК. Далее выполните команду Сервис/Анализ данных. Выберите инструмент анализа Регрессия из списка Инструменты анализа. Щелкните по кнопке ОК. На экране появится диалоговое окно Регрессия (рис.4). в текстовом поле ВХОДНОЙ ИНТЕРВАЛ Y введите диапазон со значениями зависимой переменной $C$2:$C$21. в текстовом поле ВХОДНОЙ ИНТЕРВАЛ Х введите диапазон со значениями независимых переменных $В$2:$В$21. Убедитесь, что в поле Уровень надежности введено 95 % и переключатель Параметры вывода установлен в положении Новый рабочий лист. Щелкните по кнопке ОК. 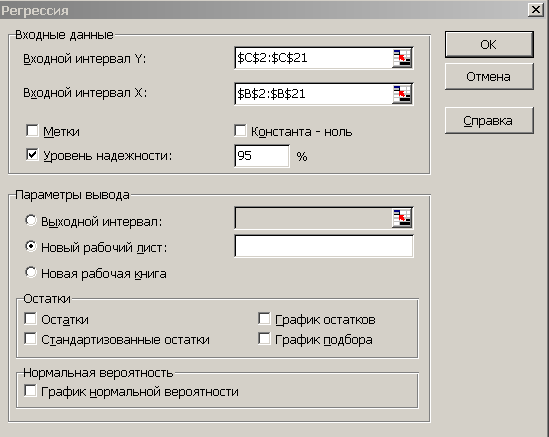 Рис. 4 Диалоговое окно инструмента анализа Регрессия. В результате на новом листе будет отображены результаты использования инструмента Регрессия (рис.5). 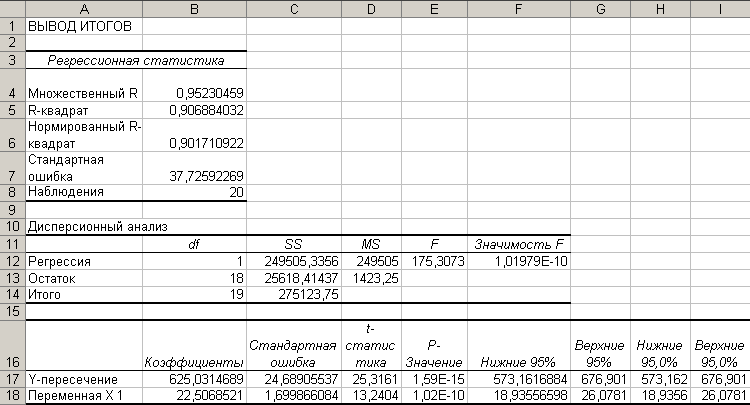 Рис. 5. Вывод итогов инструмента Регрессия. Среди полученных результатов после применения инструмента Регрессия есть столбец «Коэффициенты», содержащий значение b в строке «Y-пересечение», а – в строке «Переменная Х1». Сравните полученные результаты с ранее рассчитанными коэффициентами a и b. Обратите также внимание на следующие показатели: Столбец df - число степеней свободы (используется при проверке адекватности модели по статистическим таблицам): в строке Регрессия находится  – количество коэффициентов уравнения, не считая свободного члена b; в строке Остаток находится  =n- -1, где n – количество исходных данных.Столбец SS (сумма квадратов): в строке Регрессия: SS   = ,где  - модельные значения Y, полученные путем подстановки значений Х в построенную модель;  - среднее значение Y;в строке Остаток:  .Столбец MS - вспомогательные величины: в строке Регрессия:  ; в строке Остаток:  .Столбец F - критерий Фишера. Используется для проверки адекватности модели: 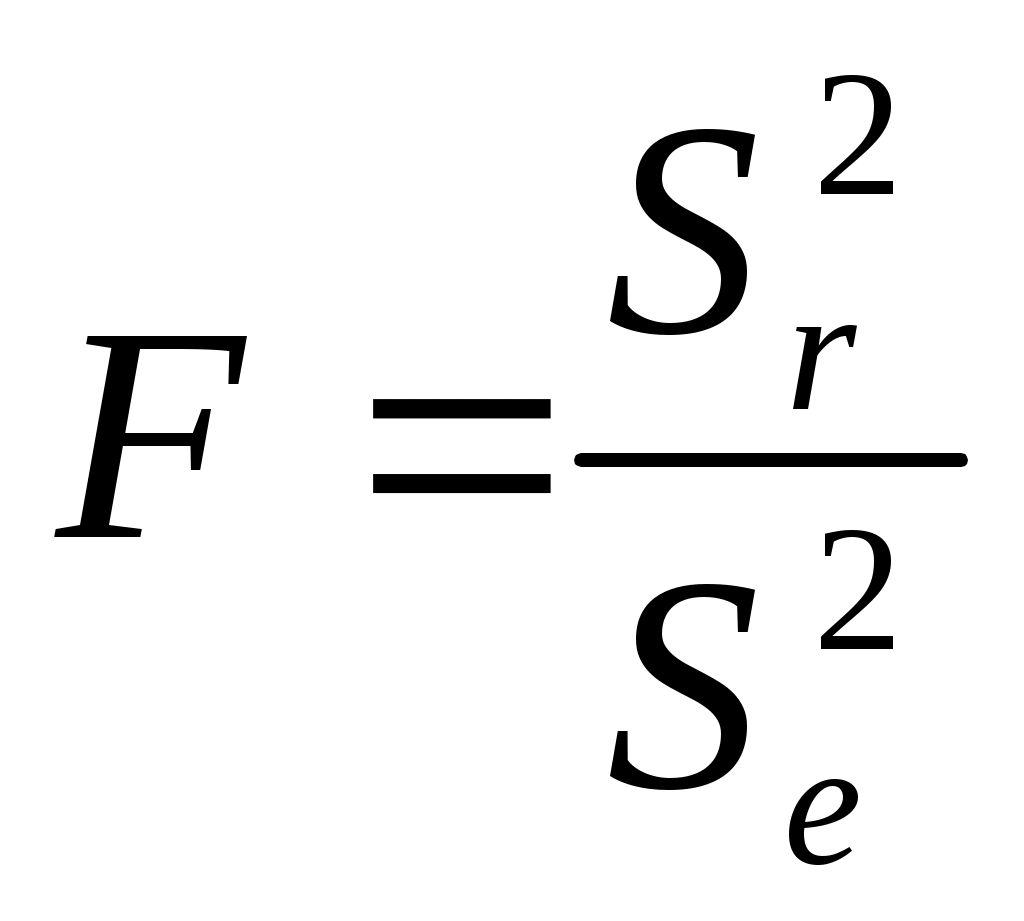 .Столбец Значимость F - оценка адекватности построенной модели. Находится по значениям F, и с помощью функции FРАСП. Если Значимость F меньше 0,05, то модель может считаться адекватной с вероятностью 0,95.Стандартная ошибка, t-статистика - это вспомогательные величины, используемые для проверки значимости коэффициентов модели. Р - величина - оценка значимости коэффициентов модели. Если Р - величина меньше 0,05, то с вероятностью 0,95 можно считать, что соответствующий коэффициент модели значим (т.е. его нельзя считать равным нулю и Y значимо зависит от соответствующего Х). Нижние и верхние 95 - доверительные интервалы для коэффициентов модели. Задание 3. Выбор наиболее точной модели связи. Условие задачи. Исследуется зависимость дозы облучения от толщины слоя защитного материала. Имеются результаты 10 экспериментов (см. рис.6). Имеются основания предполагать, что зависимость дозы (функция) от толщины слоя материала (аргумент) может выражаться одним из следующих уравнений: Y=A0 + A1*X (линейная модель); Y=A0*  (степенная модель);Y=A0+A1/X (гиперболическая модель). Выберите наиболее точную модель и определите ее коэффициенты. 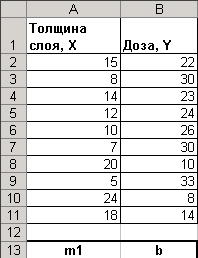 Рис.6 Исходные данные. Создайте на новом листе таблицу согласно рис. 6. Постройте на этом же листе точечную диаграмму зависимости Y=f(X). Нанесите на нее линейный и степенной тренды с уравнениями и величиной достоверности аппроксимации ( ).Для построения гиперболической модели преобразуйте модель в линейную, получив в ячейках С2:С11 величину 1/Х. А в ячейку С1 введите заглавие: «Величина U=1/X». Используя функцию ЛИНЕЙН, получите в ячейках А14:В14 коэффициенты уравнения m1 и b (т.е. уравнение Y= b+m1*U). В ячейку A16 введите заголовок «Гиперболическая модель». В ячейку A17 введите уравнение Y= b+m*x (вместо b и m укажите конкретные числа). Для построенной гиперболической модели найдите величину достоверности аппроксимации. Для этого найдите сначала среднее значение c помощью функции СРЗНАЧ в ячейке D2. В ячейку D1 введите заглавие «Ср. знач. Y».В столбце E2:E11 получите модельные значения  путем подстановки значений U из блока ячеек С2:С11 в построенную модель. Для этого в ячейку E2 введите формулу =$B$14+$A$14*C2. Скопируйте формулу вниз в смежные ячейки. В ячейку E1 введите заголовок: «Модельные значения Y».Найдите сумму квадратов  , скорректированную на среднее: . Для этого в столбце F2:F11 получите разность  . В ячейку F1 введите заголовок: «Yi-Ycp.».В столбце G2:G11 получите квадраты разностей, а в ячейку G1 введите заголовок: «(  ».В ячейке Н2 получите итоговую сумму, а в ячейку Н1 введите заголовок: «SSy». Аналогичным образом найдите сумму квадратов прогнозируемых (модельных) значений, скорректированную на среднее  . Для этого используйте столбцы I, J, K.Найдите величину достоверности аппроксимации:  в ячейке L2.По значениям коэффициентов достоверности аппроксимации выберите наиболее точную модель, которая соответствует максимальному коэффициенту достоверности. Копия экрана Задания 3. приведена на рис. 7. 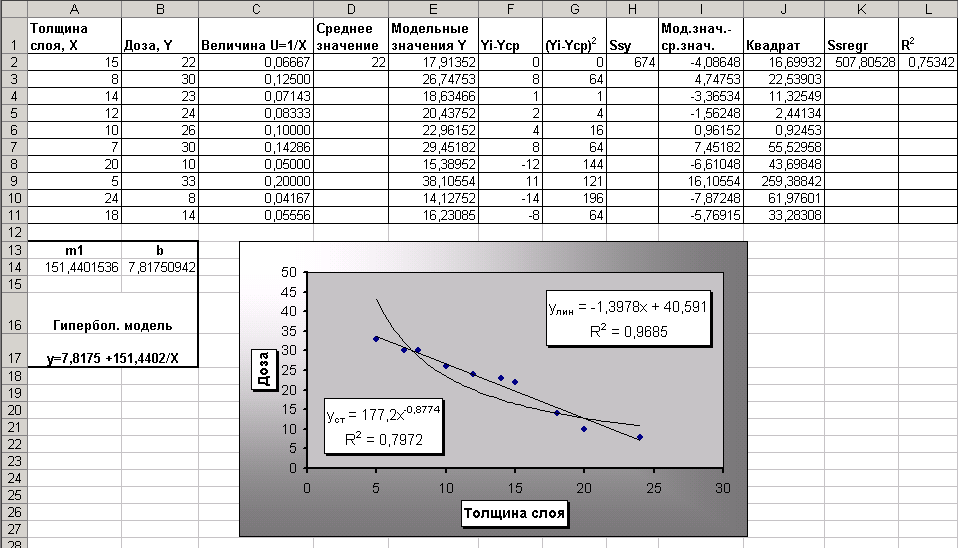 Рис. 7. Расчеты гиперболической модели. Проверьте правильность вычислений, воспользовавшись инструментом анализа Регрессия. Задания для самостоятельной работы. 1. Имеются данные по двум экономическим показателям X и Y. Необходимо: Вычислить коэффициент корреляции. Построить корреляционное поле. Построить регрессионную модель (с использованием функции ЛИНЕЙН).
2. Установить, зависит ли количество посетителей музея и посетителей парка от числа ясных дней за определенный период. Для этого: Вычислить коэффициенты корреляции. Построить корреляционное поле. Построить регрессионную модель (графическим способом и с помощью инструмента Регрессия).
|