Лабрадора 89. лабораторная 27 1996. Лабораторная работа 27. Printed by Shtin Alex sass inc. Tel 284858. Уральский Государственный Технический Университет
 Скачать 159 Kb.
|
|
Лабораторная работа № 27. Printed by Shtin Alex SASS IncÓ. Tel 28-48-58. Уральский Государственный Технический Университет УГТУ - УПИ им. С.М.Кирова ОТЧЁТ По лабораторной работе № 27. “ Изучение явления поляризации света.” Студент: Косяков Иван Группа:Р- 160 Дата:. ã Екатеринбург 1996 г. Свет естественный и поляризованный. 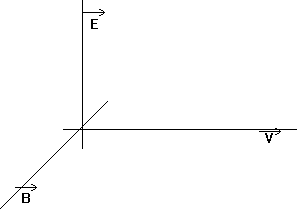 Рис. 1 Правовинтовая система трех векторов. Свет имеет электромагнитную природу. Световые волны поперечны : электрический вектор  и магнитный вектор  располагаются в плоскости, перпендикулярной к направлению распространения  волны, образуя правую тройку (Рис. 1).Оптические явления обусловлены действием, главным образом, вектора 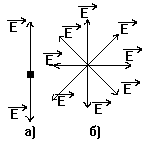, который обычно в таких случаях называют световым вектором, и при графическом описании световой волны изображают закон изменения только вектора . Рис. 2 Направление колебаний вектора Е. а)линейно-поляризованный б)неполяризованной волне Согласно теории Максвелла электромагнитные волны в общем случае должны быть эллиптически поляризованными, т.е. конец вектора 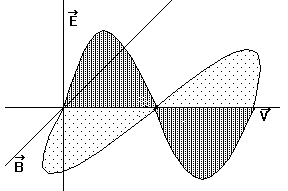(и соответственно ) описывает эллипс, вырождающийся в частных случаях в окружность (круговая поляризация) или в прямую (линейная поляризация). В случае линейно поляризованного света в данной точке колебание вектора происходит вдоль прямой, положение которой в пространстве фиксировано, с течением времени не изменяется (Рис. 2,а ). Рис. 3 Схема распространения плоскополяризованной волны. В случае так называемого естественного света, испускаемого всеми реальными источниками, кроме ЛАЗЕРов, вектор колеблется вдоль прямой, положение которой с течением времени хаотически меняется, оставаясь, однако, перпендикулярным вектору (Рис. 2,б ); вектор в каждый данный момент перпендикулярен к .Схематически картину распространения плоскополяризованной волны иллюстрирует Рис. 3. Из него видно, что во всех точках вдоль луча колебания электрического вектора происходит в одной и той же плоскости, проходящей через луч и не меняющей своего положения в пространстве. Эта плоскость называется плоскостью поляризации.Поляризованные лучи можно получить, например, пропуская естественный свет через оптически анизотропные cреды. Так называют вещества, у которых показатель преломления по разным направлениям имеет различные значения, например, некоторые виды кристаллов. Оптические cреды, в которых показатель преломления имеет одно и то же значение по всем направлениям, являются изотропными. К ним относятся кубические кристаллы. Линейно поляризованные лучи можно получить также при отражении или преломлении света на границе двух диэлектриков. Получение света, поляризованного по эллипсу и кругу. 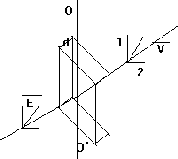 Рис. 4 Угол между обыкновенным и необыкновенным лучами, образовавшимися в результате двойного лучепреломления, может быть равным нулю. Так бывает в том случае, когда падающий луч перпендикулярен кристаллической пластинке, вырезанной из одноосного кристалла параллельно оптической оси ОО’ (Рис. 4). Здесь явление двойного лучепреломления сводится к распространению с различной скоростью вдоль одного направления, являющегося продолжением падающего луча, двух волн. Если падающий луч был линейно поляризован, то обыкновенный и необыкновенный лучи будут когерентны, и на выходе из кристалла они будут иметь разность хода D = (no- ne)d и соответсвующую разность фаз dj =  (no- ne)d .Поскольку у обыкновенного и необыкновенного лучей колебания вектора происходят во взаимно перпендикулярных направлениях с одной и той же частотой. а после выхода из кристалла и с постоянной разностью фаз dj, то, как известно из теории колебаний, конец результирующего вектора , в общем случае, будет описывать эллипс, т.е. линейно поляризованный свет после прохождения такой кристаллической пластинки становится эллиптически поляризованным.В том случае, когда амплитуды складываемых колебаний равны (это будет, когда вектор падающего луча составляет угол 45° с осью ОО’), а толщина пластинки такова, что разность фаз складываемых колебаний равна  +2pm , эллипс вырождается в окружность.Толщина d пластинки, удовлетворяющая этому, находится из условия (n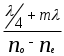o- ne)d = +2pm ,d =  , где m - любое целое число. Такие пластинки называются “пластинками в четверть волны”. Пластинка в  , естественно, рассчитывается на определённую длину волны.Таким образом, для получения света, поляризованного по кругу, необходима пластинка “в четверть волны” и линейно поляризованный монохроматический свет ; эта же пластинка может быть использована для получения эллиптически поляризованного света. Экспериментальная часть работы. 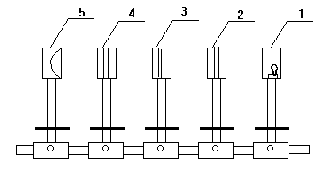 Рис. 5 Данная работа заключается в ознакомлении с некоторыми способами получения света с заданным состоянием поляризации (линейно поляризованного, поляризованного по кругу и эллиптически поляризованного) и методами анализа поляризованного света. Она представляет собой оптическую скамью, на которой смонтирован источник света (фонарь с проекционной лампой, конденсором и светофильтром), ползунки с установленными на них поляроидами (поляризатор 2 и анализатор 4), между которыми помещается пластинка “в четверть волны”. Поляроид, анализатор и пластинка установлены во вращающихся оправах с лимбом. Фотоэлемент 5 служит для измерения интенсивности света (Рис. 5). Приборы и материалы:
Проверка закона Малюса. Закон Малюса: I=I0cos2j Проводим измерения по плану, результаты заносим в таблицу:
По данны таблицы строим график (см. вкладку). Получение и анализ света, поляризованного по кругу. Скрестить поляризатор и анализатор (т.е. вращением анализатора добиться минимума фототока). Между скрещёнными поляризатором и анализатором установить пластинку .Вращая пластинку на один полный оборот, можно найти четыре ориентации пластинки, при которых интенсивность света, прошедшего через систему, имеет максимальное значение. Об этом можно судить по максимуму тока на микроамперметре. Каждая из этих ориентаций даёт возможность получить свет, поляризованный по кругу.Затем поворачивают анализатор и через каждые 20° измеряют величину фототока на протяжении одного полного оборота анализатора. Строят в полярных координатах график распределения интенсивности света (по величине фототока) и сравнивают его форму с теоретической (окружностью). Проведём измерения результаты которых занесём в таблицу:
По данным таблицы построим график. В идеале это должна быть окружность (см. вкладку). Получение и анализ эллиптически поляризованного света. Изменяют найденную для получения круговой поляризации ориентацию пластинки , лучше всего, на +20° или -20°. Вращая анализатор на полный оборот, измеряют, как и в предыдущем случае, величину фототока и строят график распределения интенсивности света в зависимости от угла a между осями пропускания поляризатора и анализатора.Максимумы и минимумы этой кривой распределения интенсивности всегда промеряются многократно, т.к. именно они используются для перехода от кривой распределения интенсивности к эллипсу распределения амплитуды. Поскольку для получения эллиптически поляризованного света в работе используется пластинка в четверть волны, создающая разность фаз складываемых колебаний, равную +2pm , то эллипс, описываемый концом вектора , будет ориентирован в осях, одной из которых будет направление оптической оси ОО’. На графике, изображающем результаты измерений, оси этого эллипса направлены по максимальной и минимальной хордам полученного графика. Отношение полуосей эллипса можно найти, извлекая квадратный корень из соотношения этих длин, т.к. интенсивность пропорциональна квадрату амплитуды вектора . Зная отношение полуосей эллипса и их ориентацию, в произвольном масштабе строят эллипс.Проведя измерения, составим таблицу:
По данным этой таблицы можно построить кривую (см.вклаку). Вывод: В данной лабораторной работе Я изучал явление поляризации света. При этом Я провёл три эксперемента выявляющие осносвные свойства и особенности поляризованного сваета. Результаты моих измерения Я предтавил в двух видах: таблице и графически. Первый способ удобен для работы с ЭВМ, а второй нагляден для человека. В результае работы получились некоторые отклонения от теоретических расчётов (закон Малюса). Это отклонения, Я думаю, можно объяснить неполной совершенностью аппаратуры нашей Лаборатории по сравнению с аналогичной лабораторией Малюса. |