14_15_Лабораторная работа 3-4_МОДЕЛИРОВАНИЕ РАВНОВЕСИЯ ПОТРЕБИТЕ. Лабораторная работа 34 моделирование равновесия потребителя в рамках ординалистского подхода в ms excel
 Скачать 47.96 Kb. Скачать 47.96 Kb.
|
|
Лабораторная работа 3-4 МОДЕЛИРОВАНИЕ РАВНОВЕСИЯ ПОТРЕБИТЕЛЯ В РАМКАХ ОРДИ-НАЛИСТСКОГО ПОДХОДА В MS EXCEL 1 Задание Доход потребителя Петрова составляет I руб. в неделю. Он максимизирует полезность, покупая некоторые количества благ X и Y по рыночным ценам PX руб./шт. и PY руб./шт., соответственно. Функция полезности потребителя имеет вид TU (X,Y)=AXαYβ (функция Кобба-Дугласа). Определите набор благ, при котором потребитель максимизирует свою полезность (аналитически и графически) Для функции Кобба-Дугласа, используя возможности программного продукта Ecxel, постройте: – карту кривых безразличия; - линию бюджетного ограничения; – Кривую «цена-потребление»; – Кривую «доход-потребление». Дайте экономическую интерпретацию полученным результатам В соответствии с порядковым номером журнала выберите значения параметров функции полезности Кобба-Дугласа TU (X,Y)=AXαYβ для двух товаров, доход, цены товаров X и Y (преподаватель может изменить и дополнить параметры): Численные значения параметров задачи
2 Требования к оформлению отчета Отчет по лабораторной работе должен содержать: – Лист задания, утвержденной формы – Лист отчета, утвержденной формы – Основную часть, в которой необходимо отразить: тему работы, цель работы, основные теоретические положения по теме, практическую часть с пошаговым описанием работы, таблицами и графиками, отражающими результаты работы – Выводы по работе 3 Методические рекомендации по выполнению работы 3.1 Определение оптимального набора потребителя аналитическим способом Пример задания: Определить оптимальный набор потребителя с доходом 600 руб. в неделю, который он полностью тратит на некоторые количества благ X и Y по рыночной цене 80 руб./шт. и 50 руб./шт., соответственно. Предпочтения потребителя описываются функцией Кобба-Дугласа со следующими параметрами А=2, α=1, β=0.5, таким образом, TU (X,Y)= 2X1Y0.5 Для решения данной задачи необходимо определить основные условия положения равновесия: 1 Цель: TU(X,Y)=2XY0.5=>max (1) 2 Ограничение: 80X+50Y=600 (2) 3 Условие оптимума: 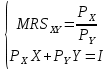 (3) (3)Первое уравнение в системе (3) представляет собой равенство желаний (MRSXY) и возможностей (PX/ PY) потребителя в точке оптимума. С геометрической точки зрения – это равенство углов наклона кривой безразличия и кривой бюджетного ограничения. Кривая безразличия – линия, объединяющая ряд наборов, одинаково предпочтительных для потребителей Второе уравнение в системе (3) – уравнение бюджетного ограничения. Бюджетное ограничение – ряд всех возможных наборов, доступных при данных ценах и доходах. Учитывая, что 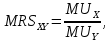 а предельная полезность каждого из благ – частные производные функции полезности 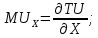 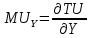 систему (3) можно записать в виде: 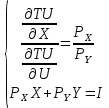 (4) (4)Решение системы уравнений (4) даст искомый результат в виде товарного набора(X*,Y*), обеспечивающего максимум полезности при данных предпочтениях, ценах на товары и доходе потребителя. Решим задачу максимизации полезности для функции Кобба-Дугласа в общем виде. Вычислим частные производные функции полезности: 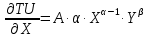 ( 6 ) ( 6 )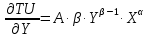 (5 ) (5 )Разделив выражение (5) на выражение (6) и приравняв отношение предельных полезностей товаров X и Y к отношению их цен (4), получим следующую систему уравнений(7) в виде: 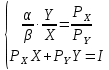 → → 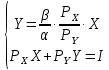 (7) (7)Подставив полученное выражение для блага Y в уравнение бюджетного ограничения, получим оптимальное количество блага X: 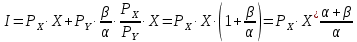 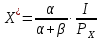 (8) (8)подставляя найденный X* в выражение для Y в системе (7), находимY* 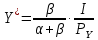 (9) (9)Найденные в общем виде X* и Y* представляют собой функции спроса на товары X и Y в зависимости от цены товара и дохода потребителя. Для функции Кобба-Дугласа при решении задачи максимизации полезности можно использовать метод доли от дохода, т.е.: 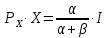 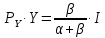 Где 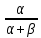 и и 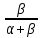 - доли дохода I, которые тратятся на блага X и Y соответственно. - доли дохода I, которые тратятся на блага X и Y соответственно.Для нашей задачи оптимальные количества благ X и Y равны: 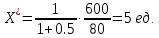 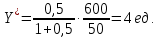 Полезность данного набора определим. Подставив данные в функцию полезности TU (X,Y)= 2X1Y0.5 TU (X,Y)= 2X1Y0.5 = 2×5×40,5 = 20 (ют.) 3.2 Определение оптимального набора потребителя графическим способом Для решения задачи графическим способом необходимо построить карту кривых безразличия и бюджетное ограничение в одной системе координат. Для того чтобы построить кривую безразличия, соответствующую уровню полезности U0, надо выразить из функции полезности Y через X и TU и придать TU значение U0: 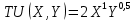 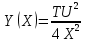 → → 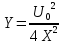 Далее задавая область определения для блага X, например, от 3 до 8 с шагом 0,5 единиц, построим кривые безразличия для разных значений TU. Построим кривые безразличия, для которых значение общей полезности потребления двух благ равняется 8, 16, 20, 32, 40. Обозначим их как U1, U2, U3, U4 и U5. Для этого создадим таблицу в программе Ecxel и рассчитаем значения Y для разных значений полезности.
Используя функцию «Вставка» построим точечную диаграмму (карту кривых безразличия). 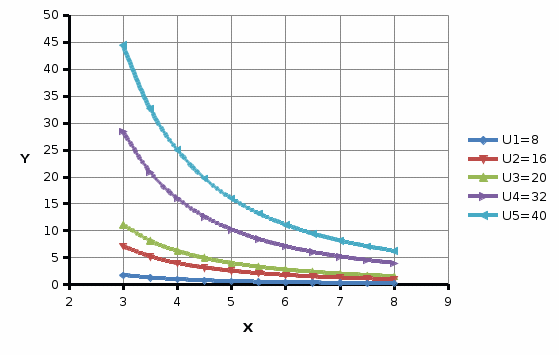 Для построения бюджетного ограничения найдем две крайние точки: на оси Х – I/Px; на оси Y – I/Py
Используя функцию «Выбор источника данных» добавим расчетные данные для отображения бюджетной линии на карте кривых безразличия. 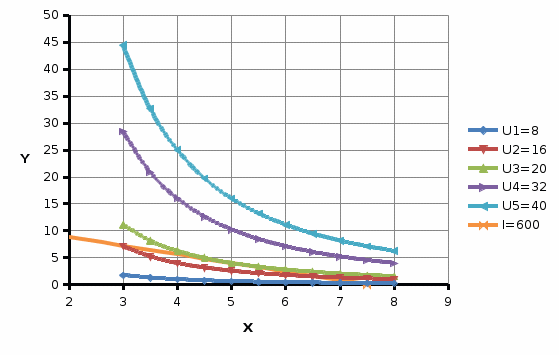 Е Точка касания E кривой безразличия с бюджетным ограничением представляет собой оптимальный потребительский набор, максимизирующий полезность потребителя. На рисунке показаны несколько кривых безразличия – U1, U2, U3, U4 и U5. Товарные наборы на кривых U1 и U2 являются доступными, но не являются оптимальными для потребителя, поскольку при том же уровне дохода потребитель может получить большую полезность, потребляя товарные наборы, соответствующие более высоким кривым безразличия. Кривые безразличия U4 и U5 выходят за пределы бюджета и поэтому недостижимы. Двигаясь вдоль бюджетного ограничения, мы находим (определяем) точку Е как точку касания кривой бюджетного ограничения с кривой безразличия наиболее высокого порядка из числа доступных - U3, в которой максимизируется полезность потребителя при данном бюджетном ограничении и предпочтениях. Полезность потребителя максимальна при потреблении 5 ед. товара Х и 4 ед. товара Y. 3.3 Построение кривой «доход-потребление» Кривая «доход-потребление» - кривая, показывающая товарные наборы, на которые предъявляется спрос при постоянных ценах на товары и различных уровнях дохода. Геометрически это линия, проходящая через оптимальные наборы благ при различных вариантах бюджетных ограничений. Уравнение кривой «доход-потребление» выводится из системы (4). Для предпочтений типа Кобба-Дугласа уравнение принимает вид: 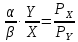 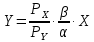 Кривая «доход-потребление» для предпочтений типа Кобба-Дугласа – луч из начала координат с углом наклона 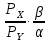 В нашей задаче уравнение для кривой «доход-потребление» имеет вид: 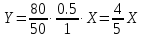 Предположим, что происходит изменение дохода потребителя, при этом цены на товар X и Y остаются неизменными. Используя формулы (8) и (9) рассчитаем оптимальные значения X и Y при доходе от 400 до 1000 с шагом 200 ден. ед.
Используя функцию «Выбор источника данных» добавим расчетные данные для отображения линии «доход-потребление» на карте кривых безразличия. 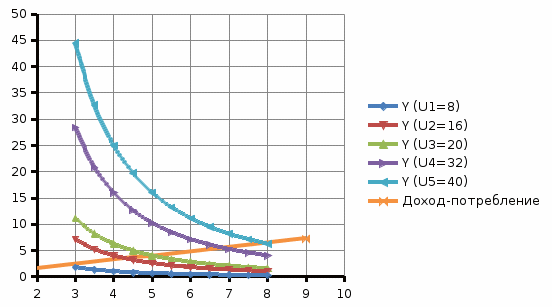 3.4 Построение кривой «цена-потребление» Кривая «цена-потребление- это множество всех оптимальных комбинаций благ X и Y при неизменном доходе и изменении цены одного из них. Геометрически это линия, соединяющая оптимумы потребителя при различных вариантах уравнения бюджетного ограничения. Так как для функции Кобба-Дугласа функции спроса X*=X*(I, PX), Y*=Y*(I, PY) зависят только от своих цен, то изменение цены одного блага не отражается на объеме потребления другого, следовательно, кривая «цена-потребление» для предпочтений типа Кобба-Дугласа параллельна оси OX и имеет уравнение Y=Y*. В нашей задаче уравнение для кривой «цена-потребление» - Y=4. Построим график с теми же кривыми безразличия, но уже с линией цена-потребление, при этом цену меняем в диапазоне от 40-120 с шагом 20.
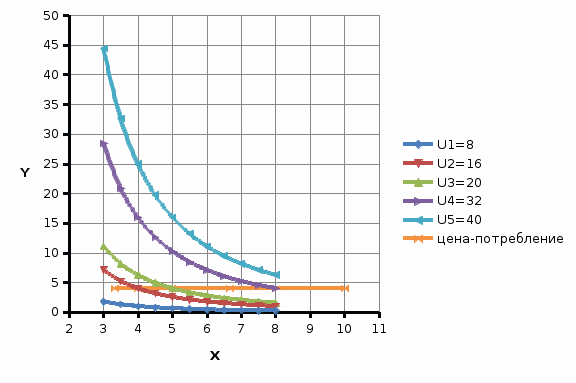 Итак, в результате выполнения работы создана модель потребительского поведения в рамках ординалисткого подхода. |
