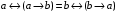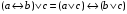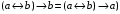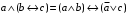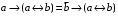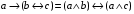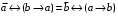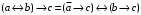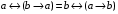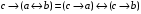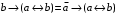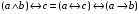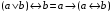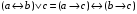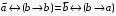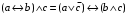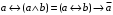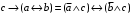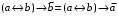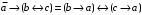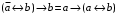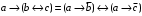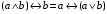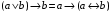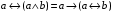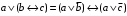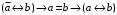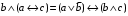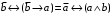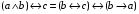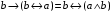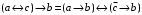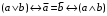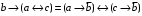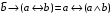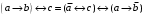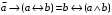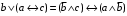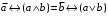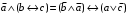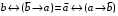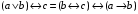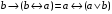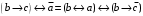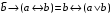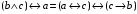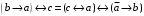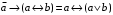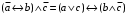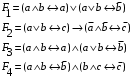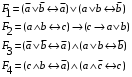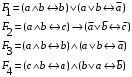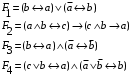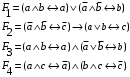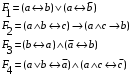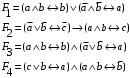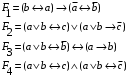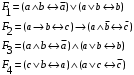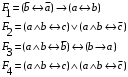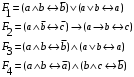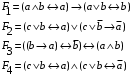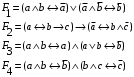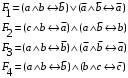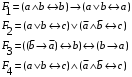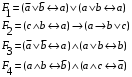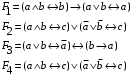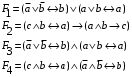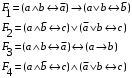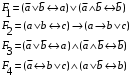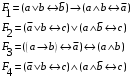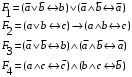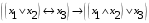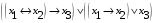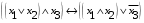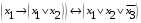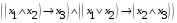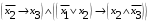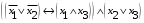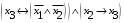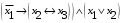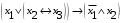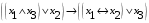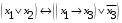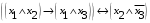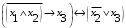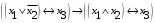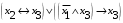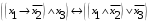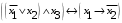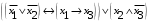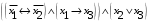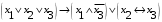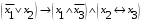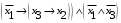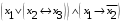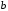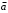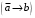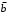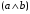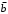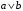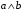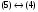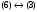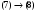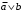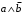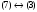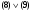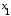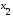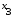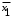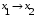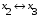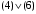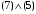Лабораторная работа №3-5. Лабораторная работа 3 алгебра логики и эквивалентные преобразования в ней. Задание 1
 Скачать 290.75 Kb. Скачать 290.75 Kb.
|
|
Лабораторная работа №3 АЛГЕБРА ЛОГИКИ И ЭКВИВАЛЕНТНЫЕ ПРЕОБРАЗОВАНИЯ В НЕЙ. Задание 1. Проверить равносильность формул алгебры высказываний: а) при помощи таблиц истинности; б) при помощи эквивалентных преобразований.
Задание 2. Для заданных функций построить таблицу истинности. Выяснить для каждой из них, является ли она тавтологией или противоречием. В иных случаях, указать для каких значений функция является выполнимой, а для каких опровержимой.
Задание 3.Построить таблицу истинности, по таблице истинности найти СДНФ, СКНФ.
Пример оформления лабораторной работы №3 Задание 1. Проверить равносильность формул алгебры высказываний: а) при помощи таблиц истинности; б) при помощи эквивалентных преобразований. 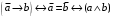 (1) (1)Решение. а) Для левой и правой части равенства составим таблицы истинности и сравним их итоговые значения на одинаковых наборах переменных: 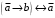 Таблица 1
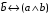 Таблица 2
По последним столбцам таблицы замечаем, что на одинаковых наборах переменных функции левой и правой частей равенства (1) принимают одинаковые значения. Следовательно, формулы эквивалентны. б) Докажем равенство (1) при помощи эквивалентных преобразований. Воспользуемся равенствами 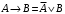 и и 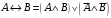 . .Преобразуем левую часть равенства (1): 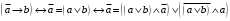 Воспользуемся правилом Де Моргана 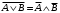 : : 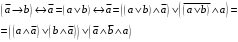 Воспользуемся законом противоречия 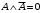 : :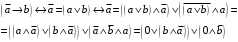 По свойству констант 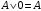 и и 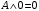 : :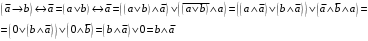 В результате получили преобразованную левую часть: 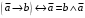 Преобразуем правую часть равенства (1): 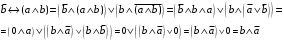 Получили: 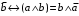 Правая и левая части равенств совпадают. Следовательно, равенства эквивалентны. Задание 2. Для заданных функций построить таблицу истинности. Выяснить для каждой из них, является ли она тавтологией или противоречием. В иных случаях, указать для каких значений функция является выполнимой, а для каких опровержимой. 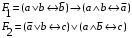 Решение. Составим таблицы истинности для функций 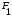 и и 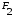 . .Для функции 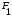 : :Таблица 1
Из последнего столбца Таблицы 1 видно, что для всех значений переменных a и b функция является опровержимой. Следовательно, функция 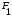 является противоречием. является противоречием.Для функции 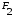 : :Таблица 2
Из последнего столбца Таблицы 2 видно, что для всех значений переменных a и b функция является выполнимой. Следовательно, функция 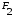 является тавтологией. является тавтологией.Задание 3.Построить таблицу истинности, по таблице истинности найти СДНФ, СКНФ. 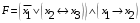 Решение. Составим таблицу истинности:
Составим совершенную дизъюнктивную нормальную форму (СДНФ) для функции 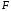 : :1. Рассмотрим все те наборы переменных, на которых функция принимает значение 1; 2. Для каждого из отобранных наборов составляют совершенную элементарную конъюнкцию (ЭК) из переменных, если 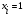 или их отрицаний, если или их отрицаний, если 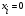 ; ;3. Из полученных ЭК составляем СДНФ. Получим: 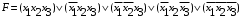 Аналогично, чтобы записать формулу логической функции в СКНФ поступим следующим образом: 1. Рассмотрим все те наборы переменных, при которых функция принимает значение 0. 2. Для каждого из отобранных наборов составляем элементарную дизъюнкцию (ЭД) из переменных если 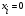 или их отрицаний, если или их отрицаний, если 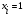 . .3. Из полученных ЭД составляем СКНФ. Получим: 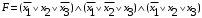 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||