Лабораторная работа 3. Лабораторная работа 3 Исследование линейных корректирующих кодов Студент группы 14в2 Носов А. В. Проверил

• Название: Лабораторная работа 3 Исследование линейных корректирующих кодов Студент группы 14в2 Носов А. В. Проверил
• Анкор: Лабораторная работа 3
• Дата: 19.04.2021
• Размер: 62 Kb.
• Имя файла: Laboratornaya_rabota_3_Nosov.doc
• Тип: Лабораторная работа; #196357

Нижегородский Государственный Технический Университет


Лабораторная работа №3
«Исследование линейных корректирующих кодов»


Выполнил:

Студент группы 14-В-2

Носов А.В.

Проверил:

Ломакин Д.В.


Нижний Новгород

2017г.

Цель работы

Исследовать построение и возможности корректирования линейных систематических кодов.

Теоретическая часть.

По теореме Шеннона существует возможность вести передачу данных по каналу с помехами со сколь угодно малой вероятностью ошибки при подходящих процедурах кодирования и декодирования.



Надежность передачи сообщений повышается за счет введения избыточности – слов, при этом каждому сообщению ставится в соответствие кодовое слово.

Корректирующие свойства кода обычно описываются расстояниями между кодовыми словами. Вес Хемминга кодового слова определяется как число ненулевых компонентов данного кодового слова при использовании линейных кодов. Для обнаружения производимых искажений, которые изменяют в передаваемых кодовых блоках не более t символов, необходимо, чтобы никакие t-кратные искажения не переводили одно кодовое слово в другое, то есть необходимо, чтобы все кодовые слова находились друг от друга на расстоянии, большем t. Для исправления t-кратных ошибок необходимо, чтобы все кодовые слова находились на расстоянии, большем, чем (2*t+1). Задача построения кода сводится к выбору из множества всех кодовых слов подмножества разрешенных кодовых слов с заданным минимальным расстоянием Хемминга между ними.

Построение проверочной матрицы.

Пусть задана последовательность чисел {7,6,3,4,2,1,5}.

На ее основе требуется построить проверочную матрицу H и уравнения кодирования.

Элемент	7	6	3	4	2	1	5
	1	1	0	1	0	0	1
Код	1	1	1	0	1	0	0
	1	0	1	0	0	1	1

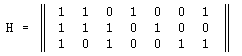Приведем матрицу H к каноническому виду: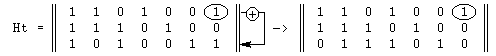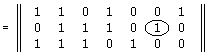




Исходя из полученной проверочной матрицы Н составляем систему уравнений:

x₁  x₂  x₄  x₇ = 0

x₂  x₃  x₄  x₆ = 0

x₁  x₂  x₃  x₅ = 0 следовательно,
x₅ = x₁  x₂  x₃

x₆ = x₂  x₃  x₄

x₇ = x₁  x₂  x₄

Информационные символы: x₁, x₂, x₃, x₄, защитные символы: x₅, x₆, x₇
Информационные символы и соответствующие им защитные:

	информационные символы	защитные символы
0	0000	000
1	0001	011
2	0010	110
3	0011	101
4	0100	111
5	0101	100
6	0110	001
7	0111	010
8	1000	101
9	1001	110
10	1010	011
11	1011	000
12	1100	010
13	1101	001
14	1110	100
15	1111	111

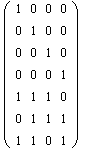Порождающая матрица G =

Проверка (декодирование по синдрому):

_ _

H y = S

1) Передаётся кодовое слово Х = | 1 1 0 1 0 0 1 |

Принятое кодовое слово Y = | 1 1 0 1 0 0 1 |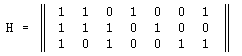



Умножаем вектор Y на проверочную матрицу
Вычисления:
1*1 + 1*1 + 0*0 + 1*1 + 0*0 + 0*0 + 1*1 = 1 + 1 + 0 + 1 + 0 + 0 + 1 = 0

1*1 + 1*1 + 0*1 + 1*0 + 0*1 + 0*0 + 1*0 = 1 + 1 + 0 + 0 + 0 + 0 + 0 = 0

1*1 + 1*0 + 0*1 + 1*0 + 0*0 + 0*1 + 1*1 = 1 + 0 + 0 + 0 + 0 + 0 + 1 = 0
|0|

Вывод: синдром S = |0|

|0|
вектор ошибки E = | 0 0 0 0 0 0 0 0 |

ошибка не обнаружена
2) Передаётся кодовое слово Х = | 1 1 0 1 0 0 1 |

Принятое кодовое слово Y = | 1 1 1 1 0 0 1 |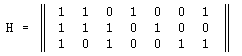



Умножаем вектор Y на проверочную матрицу

Вычисления:
1*1 + 1*1 + 1*0 + 1*1 + 0*0 + 0*0 + 0*1 = 1 + 1 + 0 + 1 + 0 + 0 + 1 = 0

1*1 + 1*1 + 1*1 + 1*0 + 0*1 + 0*0 + 1*0 = 1 + 1 + 1 + 0 + 0 + 0 + 0 = 1

1*1 + 1*0 + 1*1 + 1*0 + 0*0 + 0*1 + 1*1 = 1 + 0 + 1 + 0 + 0 + 0 + 1 = 1
|0|

Вывод: синдром S = |1|

|1|

вектор ошибки E = | 0 0 1 0 0 0 0 0 |, указывает на ошибку в третьем

разряде (обнаружена ошибка в позиции x₃)