Лабораторная работа 3 Оценка устойчивости дискретных систем управления (алгебраический и частотный критерии Михайлова) вариант 1 по дисциплине Методы анализа и синтеза систем

• Название: Лабораторная работа 3 Оценка устойчивости дискретных систем управления (алгебраический и частотный критерии Михайлова) вариант 1 по дисциплине Методы анализа и синтеза систем
• Дата: 11.01.2022
• Размер: 77.27 Kb.
• Имя файла: LR_3_Yakovlev_Sergey.docx
• Тип: Лабораторная работа; #328021

_{Высшая школа печати и медиаиндустрии}

Кафедра «Полиграфические системы»


Лабораторная работа № 3

Оценка устойчивости дискретных систем управления (алгебраический и частотный критерии Михайлова)


вариант №1
по дисциплине «Методы анализа и синтеза систем»

Выполнил(а):	Яковлев Сергей
	Артемьевич
Номер зачетной книжки	Пр1-18И-388
Группа	191-731
Институт (факультет)	принтмедиа и информационных технологий (ИПИТ)
Проверил(а):	Винокурова О.А.

2021 г.

1. 
   Расчет передаточной функции замкнутой системы.
   

1. 
   По варианту задана передаточная функция, которая, имеет следующий вид: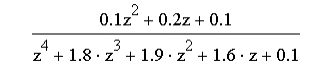
   

2. 
   Расчет дискретной передаточной функции замкнутой системы: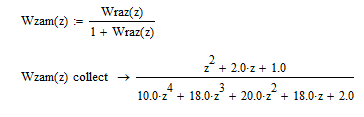
   
3. 
   Разделим знаменатель на 50 и получим характеристическое уравнение: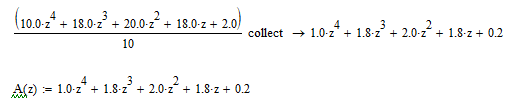
   

2. 
   Алгебраический метод оценки устойчивости системы (критерий Гурвица).
   

1. 
   Произведем замену в характеристическом уравнении на .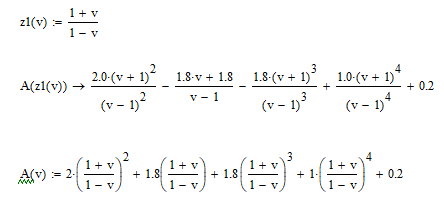
   
2. 
   Далее приводим выражение к общему знаменателю и выделяем числитель.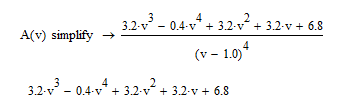
   
3. 
   Применяем критерий Гурвица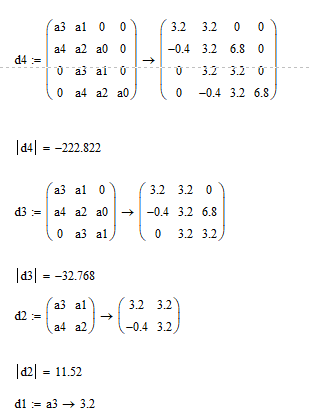
   

Так какне все коэффициенты больше нуля, следовательно, система является неустойчивой

3. 
   Частотный метод оценки устойчивости системы (критерий Михайлова).
   

1. 
   Характеристический многочлен имеет вид: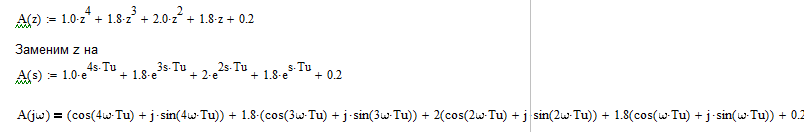
   

2. 
   Группируем по j=√-1: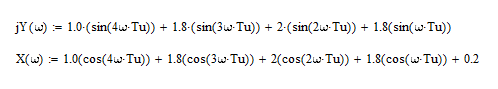
   

3. 
   Построим годограф: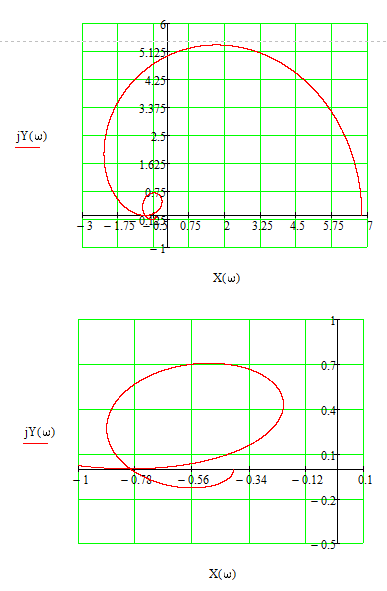
   

Вывод:по критериям Гурвица и Михайлова система является неустойчивой