Лабораторная работа 3 по Основам математического моделирования при бурении Нигс преподаватель В. А. Жигарев подпись, дата инициалы, фамилия
 Скачать 0.68 Mb.
|
|
Федеральное государственное автономное образовательное учреждение высшего образования «СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ» Институт нефти и газа институт Бурение нефтяных и газовых скважин кафедра ЛАБОРАТОРНАЯ РАБОТА №3 по Основам математического моделирования при бурении НиГС Преподаватель В.А. Жигарев подпись, дата инициалы, фамилия Студент ГБ18-01Б Е.А. Корниенко номер группы, зачетной книжки подпись, дата инициалы, фамилия Студент ГБ18-01Б И.Л. Люблинский номер группы, зачетной книжки подпись, дата инициалы, фамилия Красноярск 2021 Метод половинного деления. Цель работы: Получить базовые знания вычисления корня методом хорд. Краткие теоретические сведения: Пусть на отрезке  функция непрерывна, принимает на концах отрезка значение разных знаков, а производная  сохраняет знак. В зависимости от знака второй производной возможны следующие случаи расположения кривых (рис. 6, рис. 7).Случай 1. Функция возрастает (f(a) <0, f(b) >0, f '(x)>0).  b) Рис. 1. Расположение кривых при возрастающей функции. Кривая выпукла вниз f ''(x) > 0; Кривая выпукла вверх f ''(x) < 0; Случай 2. Функция убывает (f(a)>0, f(b)<0, f '(x)<0). 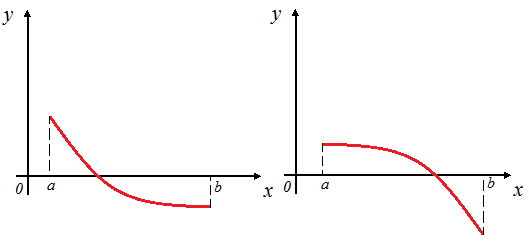 b) Рис. 2. Расположение кривых при возрастающей функции. a)Кривая выпукла вниз f ''(x) > 0; b) Кривая выпукла вверх f ''(x) < 0; Алгоритм приближенного вычисления корня методом хорд. Исходные данные: f (x) – функция; ε – требуемая точность; x0 – начальное приближение. Результат: xпр – приближенный корень уравнения f (x) = 0. Метод решения: Случай 1: и  имеют одинаковые знаки (рис. 8). Рис. 3. Геометрическая интерпретация метода хорд для случая  .График функции проходит через точк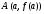и  и  . Искомый корень уравнения (точка x*) нам неизвестен, вместо него возьмет точку х1 пересечения хорды АВ с осью абсцисс. Это и будет приближенное значение корня.В аналитической геометрии выводится формула, задающая уравнение прямой, проходящей через две точки с координатами (х1; у1) и (х2; у2):  .Тогда уравнение хорды АВ запишется в виде:  .Найдем значение х = х1, для которого у = 0:  .Теперь корень находится на отрезке  . Применим метод хорд к этому отрезку. 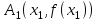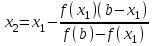Проведем хорду, соединяющую точки  и , и найдем х2 - точку пересечения хорды А1В0 с осью Ох:  .Продолжая этот процесс, находим:  .Получаем рекуррентную формулу вычисления приближений к корню  .В этом случае конец b отрезка остается неподвижным, а конец a перемещается.Таким образом, получаем расчетную формулу метода хорд: ;  .Вычисления очередных приближений к точному корню уравнения продолжается до тех пор, пока не достигнем заданной точности, т.е. должно выполняться условие:  , где  - заданная точность.Случай 2: 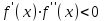 первая и вторая производные имеют разные знаки (рис. 9). Рис. 4. Геометрическая интерпретация метода хорд для случая 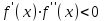.Соединим точки  и хордой АВ. Точку пересечения хорды с осью Ох будем считать первым приближение корня. В этом случае неподвижным концом отрезка будет являться конец а.Уравнение хорды АВ:  .Отсюда найдем  , полагая y = 0:  .Теперь корень уравнения  . Применяя метод хорд к этому отрезку, получим  .Продолжая и т.д., получим  .Расчетные формулы метода: ,  .Условие окончания вычислений: . Тогда хпр = xn+1с точностью .Тестовое задание: f(x)=cos(2x) +x -5  Рис.5. Пример задания Решение нашего варианта 2: f(x)=cos(πx)-x  Рис.6. Решение варианта 2  Рис.7. Решение варианта 2 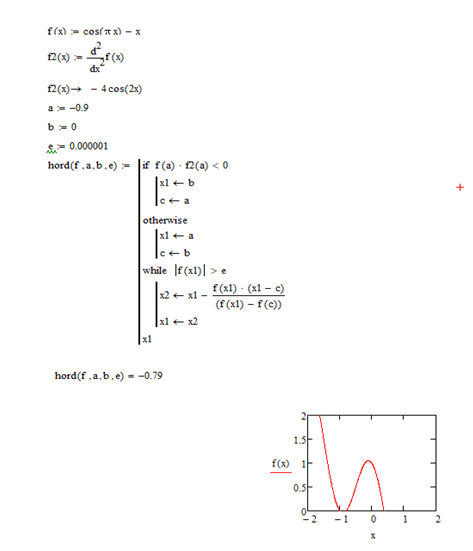 Вывод: Получил базовые знания вычисления корня методом хорд. |