Лаба номер 3. Лабораторная работа 3. Прямая геодезическая засечка
 Скачать 23.55 Kb. Скачать 23.55 Kb.
|
Лабораторная работа №3.Прямая геодезическая засечка.В лабораторных условиях прямую геодезическую засечку решают двумя способами: графоаналитическим и непосредственным. Для решения прямой геодезической засечки графоаналитическим способом на план поверхности в масштабе 1:2000 по известным координатам ХI, YI, ХII, YII, ХIII, YIII нанесем пункты опорной сети. Координаты пунктов опорной сети.
Для расчета координат точки Р1 необходимо на исходных пунктах I, II, III измерить углы r1 и r2 в одном треугольнике и r3 и r4 во втором. Дополнительно, для повышения точности расчета, берутся значения углов 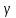 1, 1, 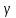 2. Сумма углов в треугольнике уравнивается к 180. 2. Сумма углов в треугольнике уравнивается к 180.Из треугольника I-II-P1. Исходные данные для вычисления координат пункта Р1 из треугольника II-III-P1.
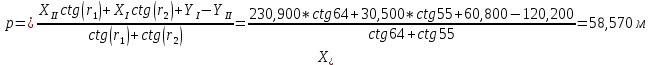 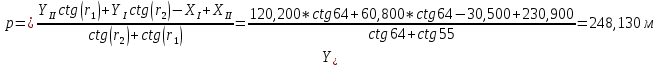 Контроль: 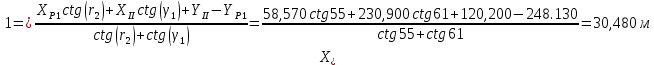 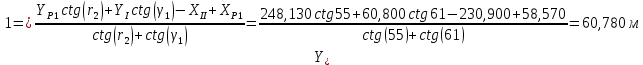 Из треугольника III-IV-P1. Исходные данные для вычисления координат пункта Р1 из треугольника II-III-P1.
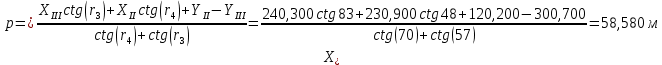 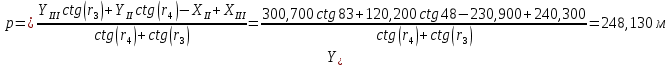 Из решения двух треугольников разница в координатах точки Р1 составляет 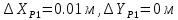 , ,которая не превышает 0,6 мм на плане в масштабе съёмки (0,12м) Среднее значение координат точки Р1 из двух треугольников: XP1=58,575 м, YP1=248,130 м. Оценка точности планового положения пункта Р1 характеризуется среднеквадратической погрешностью относительно пунктов опорной сети, величина которой не должна превышать 0,4 мм на плане в масштабе съемки /1/ (для масштаба 1:2000 Мр<=0,8м): Для треугольника II-III-P1 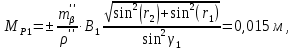 Для треугольника III-IV-P1. 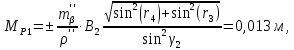 Где 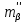 - средняя квадратическая ошибка измерения углов, принимаем - средняя квадратическая ошибка измерения углов, принимаем 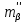 =15. =15.В1=140,500, В2=90,000 – базис прямой засечки (расстояние между пунктами опорной сети) определяется решением обратной геодезической засечки. В результате средняя квадратическая погрешность положения пункта Р1 относительно пунктов опорной сети из двух треугольников составила 0,014 м, и не превышает допустимой величины (0,8 м). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||