Лабораторная работа 3. Лабораторная работа 3 Сложение двоичных чисел. Сумматор

• Название: Лабораторная работа 3 Сложение двоичных чисел. Сумматор
• Дата: 23.11.2020
• Размер: 198.5 Kb.
• Имя файла: Лабораторная работа 3.doc
• Тип: Лабораторная работа; #153149

Лабораторная работа № 3 Сложение двоичных чисел. Сумматор

Цель: Рассмотреть основные принципы построения сумматоров. Знать сложение многоразрядных чисел. Реализация на логических элементах и в виде готовых микросхем.

План:

1. 
   Изучение теоретической части
   
2. 
   Построение схемы в программе WorkBench
   

Ход выполнения работы
Ответы на контрольные вопросы

1. 
   Дайте определение полусумматора, сумматора.
   

Полусумматор – это узел ЭВМ, выполняющий суммирование двух одноразрядных двоичных чисел. Эти числа являются разрядами двух многоразрядных двоичных кодов.

Полусумма́тор — комбинационная логическая схема, имеющая два входа и два выхода (двухразрядный сумматор, бинарный сумматор). Полусумматор позволяет вычислять сумму A+B, где A и B — это разряды (биты) обычно двоичного числа, при этом результатом будут два бита S и C, где S — это бит суммы по модулю 2, а C — бит переноса.

Существуют сумматоры и полусумматоры работающие не в двоичной логике.

Отличается от полного сумматора тем, что не имеет входа переноса из предыдущего разряда. Для построения полного сумматора необходимо иметь дополнительный вход переноса из предыдущего разряда, таким образом, полный сумматор имеет 3 входа.

Двоичный полный сумматор строится из двух полусумматоров и логического элемента 2ИЛИ, именно поэтому рассматриваемая схема называется полусумматором.

Полусумматоры используется для построения полных сумматоров.

Сумма́тор - в кибернетике - устройство, преобразующее информационные сигналы (аналоговые или цифровые) в сигнал, эквивалентный сумме этих сигналов; устройство, производящее операцию сложения.

2. 
   Покажите таблицу истинности для полусумматора, сумматора, покажите уравнения для этих схем, покажите реализацию этих уравнений с помощью логических элементов.
   

Таблица истинности полусумматора

Слагаемые		Сумма S	Перенос Р
А	В
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

Из этой таблицы сразу видно, что перенос можно реализовать с помощью операции логического умножения:

P = A & B

Для определения суммы можно применить следующее логическое выражение:

S = (A v B) & ¬(A & B)
Таблица истинности полного одноразрядного сумматора

Входы			Выходы
Слагаемые		Перенос из предыдущего разряда С	Сумма S	Перенос в следующий разряд Р
А	В
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

Формула переноса получает следующий вид:

S = (A v B v С) & ¬С v (A & B &С)


Эксперимент 1

Создадим схему в программе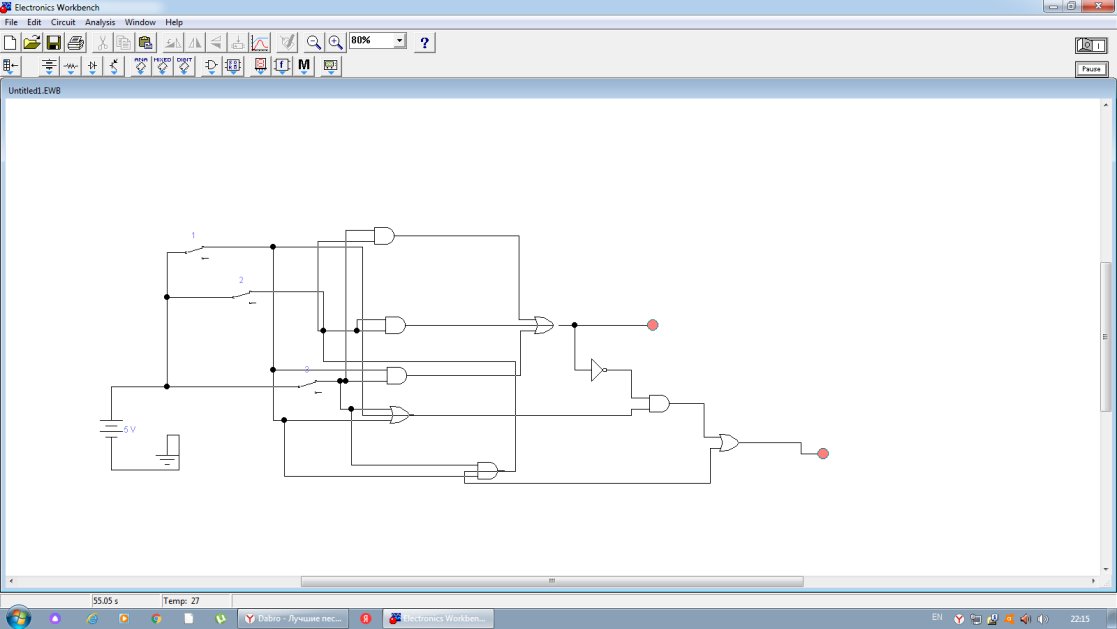



Включая и отключая ключи, если ключ замкнут, пишем в таблицу 1, иначе ставим 0. Запишем полученные результаты эксперимента в таблицу истинности сумматора.

ai	bi	pi	Si	Pi+1
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1

Эксперимент 2.

Расположим на рабочем столе программы ElectronicsWorkBench микросхему 4008 и другие компоненты для исследования сумматора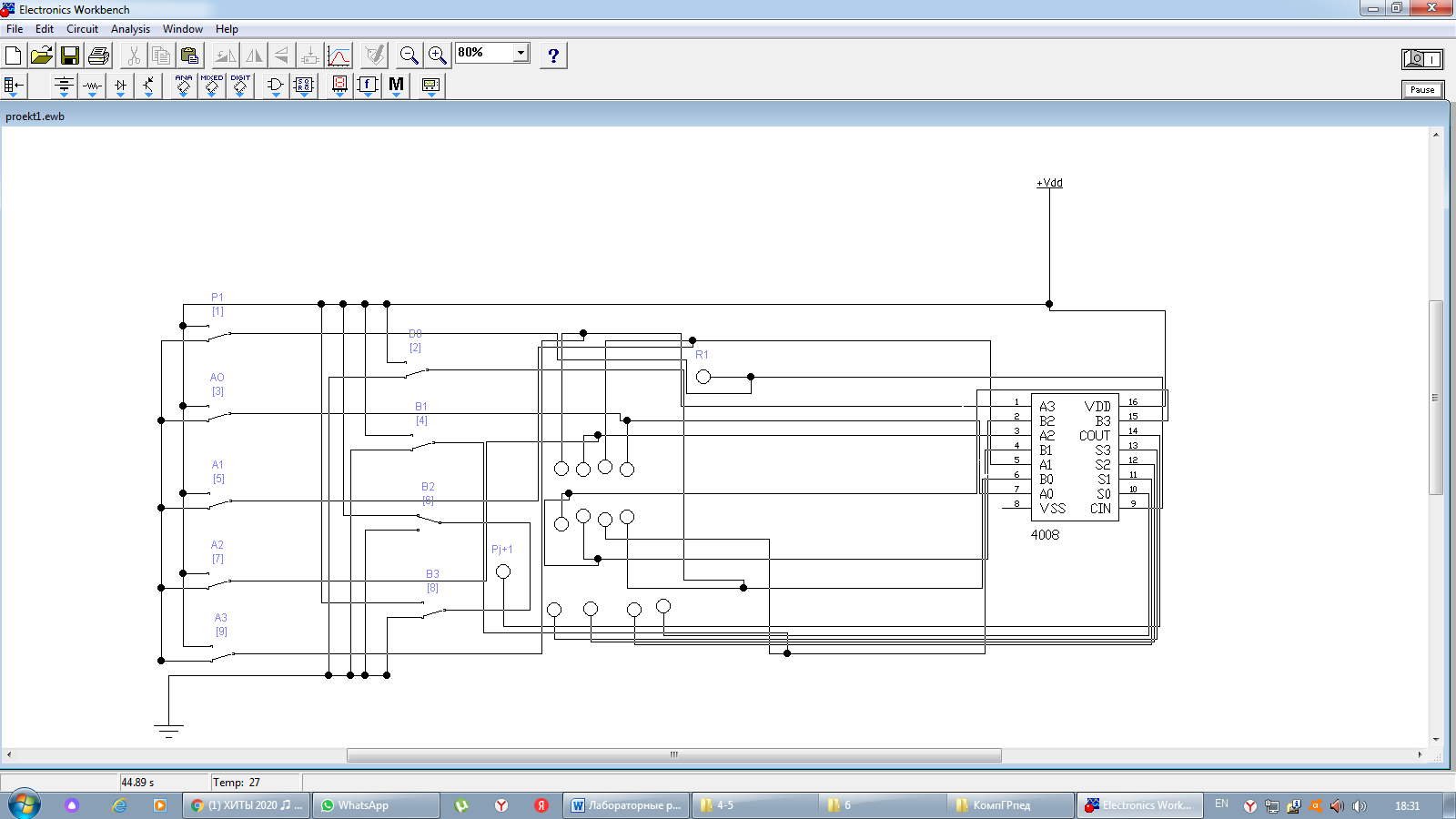


Составим для полученных результатов таблицу истинности, в последнюю колонку запишем расчетный результат:

№	Исходные данные									Результаты					Расчетный результат (двоичное 4-х или 5-ти разрядное число).
	P i СIN	А0	В0	А1	В1	А2	В2	А3	В3	S0	S1	S2	S3	Pi+1 Cout
1	0	0	1	1	1	0	1	1	0	1	0	0	0	1	10001
2	0	0	1	0	0	1	0	1	1	1	0	1	0	1	10101
3	0	1	1	0	1	1	1	0	0	0	0	1	1	0	1100

Выводы: В ходе рассмотрены основные принципы построения сумматоров. Изучен метод сложение многоразрядных чисел по средствам сумматоров, реализованных на логических элементах и в виде готовых микросхем. Произведены расчеты согласно заданным значениям. Результаты которые мы получили опытным и расчетным путем совпадают.