Технологии решения задач. Лабораторная_работа_3_Технология_решения_оптимизационных_задач (. Лабораторная работа 3 Тема Технология решения оптимизационных задач с помощью инструментария ms excel Поиск решения
 Скачать 333.5 Kb. Скачать 333.5 Kb.
|
|
Лабораторная работа № 3 Тема: Технология решения оптимизационных задач с помощью инструментария MS Excel Поиск решения. Цель: освоение инструментария Поиск решения для решения оптимизационных задач в MS Excel. Краткие теоретические сведения. Типы задач оптимизации: Задачи о перевозках: например, минимизация расходов по доставке товаров с нескольких фабрик в несколько магазинов с учетом спроса; Задачи распределения рабочих мест: например, минимизация расходов на содержание штата с соблюдением требований, определенных законодательством; Управление ассортиментом товаров: извлечение максимальной прибыли с помощью варьирования ассортиментным набором товаров (при соблюдении требований клиентов). Аналогичная задача возникает при продаже товаров с разной структурой затрат, рентабельностью и показателями спроса. Замена или смешивание материалов: например. Манипуляция материалами с целью снижения себестоимости, поддержания необходимого уровня качества и соблюдения требований потребителей. Задачи линейной алгебры: решение линейных уравнений. Мощный инструмент «Поиск решения» (Оптимизатор) предназначен для высококвалифицированного менеджера, владеющего математическими методами поиска оптимального решения сложной специальной проблемы. Процедуру поиска решения можно использовать для определения значения влияющей ячейки, которое соответствует экстремуму зависимой ячейки — например, расходы на рекламу, обеспечивающие максимальную прибыль. Влияющая и целевая ячейки должны быть связаны формулой листа, иначе при изменении значения одной не будет изменяться другая. В технологическом процессе решения линейной оптимизационной задачи с помощью Excel выделяются три типовых этапа: подготовительный (подготовка табличной модели до обращения к диалоговому окну оптимизатора, ввод данных и формул); основной (диалог с оптимизатором для определения целевой ячейки, экстремума, изменяемых ячеек, а также ограничений); заключительный (сохранение результатов текущего решения и сохранение созданной модели для возможных будущих решений). Задачи, решаемые с помощью оптимизатора, имеют три характерных признака: Имеется единственная целевая ячейка. В нее пользователь должен ввести формулу, указав позднее в программном диалоге какой экстремум необходим (максимум или минимум). После завершения построения модели и инициализации расчета программа автоматически должна добиться для этой ячейки экстремального результата. В формуле целевой ячейки должны быть сделаны ссылки на одну или более изменяемых ячеек, от значений которых зависит результат. Они могут быть названы также неизвестными или переменными для решения. Поиск решения устанавливает значения изменяемых ячеек так, чтобы найти для формулы целевой ячейки оптимальное решение. Ограничивающих ячеек может быть не менее одной на каждую изменяемую ячейку. Может существовать и некоторое количество дополнительных ячеек ограничений, например, ограничение по объему ресурса и ограничения по спросу (минимальный спрос, максимальный спрос). Элементы диалогового окна Поиск решения. 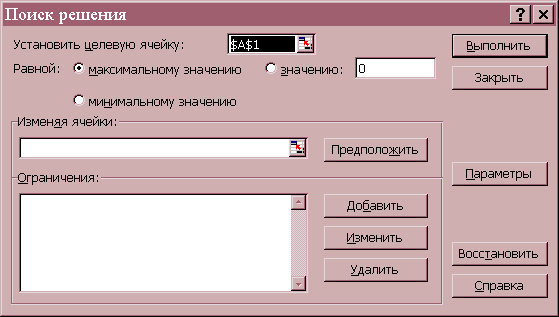 Рис. 1. Диалоговое окно Поиск решения Средство поиска решений является одной из надстроек Excel. Если в меню Сервис отсутствует команда Поиск решения, то для установки необходимо выполнить команду Сервис, Надстройки, Поиск решения. Средство поиска решений запускается командой Сервис, Поиск решения. В диалоговом окне Поиск решения в поле Установить целевую ячейку дается ссылка на ячейку с функцией, для которой будет находится максимум, минимум или заданное значение (целевую функцию). Тип взаимосвязи между решением и целевой ячейкой задается путем установки переключателя в группе Равной. Для нахождения максимального или минимального значения целевой функции этот переключатель ставится в положении Максимальному значению или Минимальному значению, соответственно. Для нахождения значения целевой функции, заданного в поле группы Равной, переключатель ставится в положение Значению. В поле Изменяя ячейки указываются ячейки, которые должны изменяться в процессе поиска решения задачи, т.е. ячейки отведенные под переменные задачи. Ограничения, налагаемые на переменные задачи, отображаются в поле Ограничения. Средство поиска решений допускает ограничения в виде равенств, неравенств, а также позволяет ввести требования целочисленности переменных. Ограничения добавляются по одному. Для ввода ограничений нажмите кнопку Добавить в диалоговом окне Поиск решения и в открывшемся диалоговом окне Добавления ограничения заполните поля. Далее нажав кнопку Добавить в диалоговом окне Добавление ограничения, введите вторую группу ограничений, налагаемых на переменные, если это необходимо. Нажатие кнопки OK завершает ввод ограничений. Обратите внимание на то, что ограничения удобнее задавать в виде диапазонов. Для задания параметров поиска решения нажмите кнопку Параметры в диалоговом окне Поиск решения. В открывшемся диалоговом окне Параметры поиска решения можно изменять условия и варианты поиска решения исследуемой задачи, а также загружать и сохранять, используемые по умолчанию.  Рис. 2. Диалоговое окно Параметры поиска решения Поле Максимальное время служит для ограничения времени, отпускаемого на поиск решения задачи. Поле Предельное число итераций служит для ограничения числа промежуточных вычислений. Поля Относительная погрешность и Допустимое отклонение служит для задания точности, с которой ищется решение. Рекомендуется после нахождения решения с величинами данных параметров, заданными по умолчанию, повторить вычисления с большей точностью и меньшим допустимым отклонением и сравнить с первоначальным решением. Использование подобной проверки особенно рекомендуется для задач с требованием целочисленности переменных. Флажок Линейная модель служит для поиска решения линейной задачи оптимизации или линейной аппроксимации нелинейной задачи. В случае нелинейной задачи этот флажок должен быть сброшен, в случае линейной задачи – установлен, т.к. в противном случае возможно получение неверного результата. Флажок Показывать результаты итерации служит для приостановки поиска решения и просмотра результатов отдельных итераций Флажок Неотрицательные значения служит для вывода и просмотра только положительных значений. Флажок Автоматическое масштабирование служит для включения автоматической нормализации входных и выходных значений, качественно различающихся по величине, например, при максимизации прибыли в процентах по отношению к вложениям, исчисляемым в миллионах рублей. Группа Оценки служит для выбора метода экстраполяции. Группа Разности служит для выбора метода численного дифференцирования. Группа Метод поиска служит для выбора алгоритма оптимизации Для того чтобы вывести отчет о результатах решения задачи выберите в диалоговом окне Результаты поиска решения требуемый тип отчета: Результаты, Устойчивость, Пределы. Задание Разработать математическую модель задачи линейного программирования по оптимизации выпуска продукции, построить компьютерную модель в среде табличного процессора, произвести расчет и всесторонний анализ исследуемой модели. Сделать выводы по проделанной работе. Технология работы Рассмотрим на примере, как с помощью средства поиска решений решаются линейные оптимизационные задачи. 1.1 Постановка задачи и построение математической модели Требуется определить план выпуска четырех видов продукции, обеспечивающий максимальную прибыль от ее реализации. На изготовление этой продукции расходуются трудовые ресурсы, сырье и финансы. С учетом рыночного спроса и производственно-технологических возможностей заданы предельные границы выпуска каждого вида продукции. Эти границы, наличие и нормы расхода ресурсов, а также маржинальная прибыль (разность между выручкой и переменными издержками) на единицу продукции приведены в таблице:
Обозначив количество выпускаемых изделий через Х1, Х2, Х3,Х4, а целевую функцию (валовую маржинальную прибыль)— через F, построим математическую модель задачи:  Левые три неравенства будем в дальнейшем называть ограничениями, а правые четыре — граничными условиями (они показывают, в каких пределах могут изменяться значения переменных). 1.2. Решение с помощью программы Excel 1.2.1 Ввод числовых данных Решим задачу, сформулированную в разделе 1.1. Для этого на рабочем листе введем ее числовые данные (рис. 1). В первой строке таблицы находится заголовок, во второй — наименования продуктов. Третья строка отведена для оптимального решения, которое после вычислений появится в ячейках ВЗ:ЕЗ (в жирной рамке). В четвертой строке в ячейках В4:Е4 заданы коэффициенты целевой функции, а ячейка F4, в рамке, зарезервирована для вычисления значения целевой функции. Строки с 6-й по 15-ю содержат коэффициенты, знаки и правые части ограничений. В столбце Лев. часть после вычислений появятся левые части ограничений, а в столбце Разница — разность правых и левых частей. Предложенная форма таблицы удобна не только для выполнения расчетов, но и для документирования результатов моделирования, а также обмена идеями и улучшения взаимопонимания при работе «в команде» — группе лиц, ответственных за принятие решений. Наглядность таблицы обеспечивается использованием заголовков, полужирного шрифта, подчеркивания текста и центрирования. Денежные величины следует представлять в денежном или финансовом формате (с указанием символа используемой валюты). 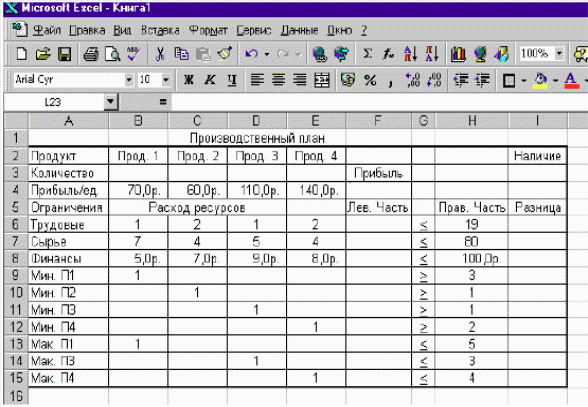 Рис. 1. Ввод данных для решения задачи линейного программирования Оформление таблицы облегчают кнопки панели форматирования, в частности: Объединить и поместить в центре (для центрирования заголовка, занимающего несколько ячеек), Денежный формат (для задания финансового формата), Увеличить разрядность или Уменьшить разрядность (для задания нужного числа дробных знаков). Чтобы отобразить знак > или <, наберите знак > или < и затем подчеркните его. После составления таблицы подберите ширину ее столбцов в соответствии с содержимым ячеек. Для этого выделите весь лист, щелкнув прямоугольник в левом верхнем углу листа (на пересечении заголовков строк и столбцов). Затем дважды щелкните правую границу заголовка любого из столбцов. 1.2.2 Ввод формул Формулы и ячейки, в которые их следует ввести, указаны в таблице:
Чтобы ввести, например, формулу для вычисления целевой функции: 1. Укажите ячейку F4. 2. В строке формул щелкните кнопку Изменить формулу (со знаком равенства). Раскроется панель формул. 3. В левой части строки формул раскройте список функций и щелк- ните имя функции СУММПРОИЗВ. Если его там нет, выберите в списке пункт Другие функции. В открывшемся окне в категории Математические найдите функцию СУММПРОИЗВ и дважды щелкните ее имя. Панель формул примет вид, позволяющий задать аргументы этой функции (рис. 2). 4. Введите аргументы функции СУММПРОИЗВ. 5. Щелкните кнопку ОК. Сразу после ввода формулы в ячейке F4 появится 0, так как формула вычисляется с нулевыми значениями переменных (ячейки ВЗ:ЕЗ пока пусты).  Рис. 2. Ввод формулы целевой функции задачи линейного программирования Функций СУММПРОИЗВ позволяет вычислить сумму произведений двух массивов, первый из которых содержит значения переменных, а второй — коэффициенты целевой функции. Чтобы указать соответствующие диапазоны, можно воспользоваться кнопками свертывания, расположенными справа от полей ввода. Они позволяют временно убрать панель формул с экрана, чтобы удобнее было выделять диапазон на листе. Закончив выделение, щелкните кнопку снова для восстановления панели. Ссылка на первый диапазон должна быть абсолютной, со знаками доллара перед каждой буквой и цифрой: $В$3:$Е$3 (чтобы изменить относительную ссылку на абсолютную, нажмите клавишу F4 непосредственно после ввода этой ссылки; если это не сделать сразу, то в дальнейшем ссылку сначала понадобится выделить и лишь затем нажать клавишу F4). Ссылка на второй диапазон В4:Е4, напротив, должна быть относительной: что понадобится в дальнейшем при копировании формулы. После ввода формулы для вычисления целевой функции необходимо задать формулы левых частей ограничений. С этой целью скопируйте формулу из ячейки F4 в ячейки F6:F15. Чтобы копировалась только сама формула (без формата ячейки, к которому относятся, например, рамка и символ используемой валюты) можно воспользоваться специальной вставкой. Для этого щелкните ячейку F4 правой кнопкой мыши и в контекстном меню выберите команду Копировать, затем выделите диапазон F6:F15, щелкните его правой кнопкой мыши и в контекстном меню выберите команду Специальная вставка. В группе Вставить открывшегося окна выберите параметр формулы и щелкните кнопку ОК. Чтобы отменить движущуюся границу ячейки F4, нажмите клавишу Esc. При копировании относительная ссылка В4:Е4 будет меняться, указывая на массивы коэффициентов соответствующих ограничений, а абсолютная — $В$3:$Е$3 — останется неизменной. Для проверки формулы вячейке достаточно дважды щелкнуть эту ячейку. Формула будет отображена на экране, ссылки на ячейки — выделены цветом, а сами ячейки — обведены рамками соответствующих цветов (после просмотра нажмите клавишу Esc). Чтобы отображались все введенные формулы, выберите вменю Сервис команду Параметры и в открывшемся окне на вкладке Вид в группе Параметры окна установите флажок Формулы. Если таблицу с формулами необходимо напечатать, подберите ширину ее столбцов в соответствии с содержимым ячеек, как это было описано ранее. Аналогично, с помощью копирования, вводятся формулы в ячейки I6:I15 для вычисления разницы правых и левых частей ограничений. Для ограничений со знаком < из правой части ограничения вычитается левая, а для ограничений со знаком > — наоборот. Таким образом, если ограничения выполняются и план допустим, то разница всегда неотрицательна. После ввода формул вы можете подставлять в ячейки ВЗ:ЕЗ любые значения (количество выпускаемой продукции), получая соответствующую величину прибыли в ячейке F4 и объем израсходованных ресурсов в столбце Лев.часть. Столбец Разница покажет, допустим ли соответствующий производственный план, какие ресурсы дефицитны (для них разница равна нулю) и каков остаток недефицитных ресурсов (он равен положительной разнице). 1.2.3 Указание целевой функции и изменяемых ячеек Теперь воспользуемся средством поиска решений. Для этого в меню Сервис выберите команду Поиск решения, которая откроет одноименное окно. При решении нашей задачи это окно должно быть заполнено, как показано на рис.3.  Рис 3. Окно средства поиска решения при решении задачи линейного программирования В окне Поиск решения вы должны задать следующие параметры: • Установить целевую ячейку— для указания целевой ячейки, зна- чение которой необходимо максимизировать, минимизировать или установить равным заданному числу. Эта ячейка должна содержать формулу для вычисления целевой функции. • Равной — для выбора варианта оптимизации значения целевой ячейки (максимизация, минимизация или подбор заданного числа). • Изменяя ячейки — для указания ячеек, значения которых изменяются в процессе поиска решения до тех пор, пока не будут выполнены наложенные ограничения и условие оптимизации значения целевой ячейки. В нашем примере это ячейки, отведенные для значений переменных. • Ограничения — для отображения списка ограничений поставлен- ной задачи. При вводе ссылок на ячейки (как и при задании аргументов функции СУММПРОИЗВ) удобно пользоваться кнопками свертывания диалогового окна, расположенными справа от соответствующих полей. 1.2.4 Добавление ограничений Дня ввода ограничений следует нажать кнопку Добавить, открывающую окно Добавление ограничения (рис. 4.).  Рис. 4. Добавление ограничения В этом окне — два поля ввода: • Ссылка на ячейку — для указания ячейки или диапазона ячеек, на значения которых необходимо наложить ограничение («левая часть ограничения»). • Ограничение — для задания условия, накладывающегося на значения ячейки или диапазона, указанного в поле Ссылка на ячейку («правая часть ограничения»). В это поле можно ввести число, формулу, ссылку на ячейку или диапазон. В раскрывающемся списке между этими полями можно выбрать необходимый знак (<=, =, >=), а также пункты цел (целое число) или двоич (двоичное число — 0 или 1), указывающие вид переменных при целочисленном решении. Для ввода ссылок на ячейки и диапазоны можно, как и раньше, воспользоваться кнопками свертывания диалогового окна, расположенными справа от полей ввода. Но поскольку окно Добавление ограничения и так достаточно невелико, удобнее просто перетащить его вниз экрана, поместив указатель мыши на заголовке. Затем следует щелкнуть в нужном поле этого окна и выделить на рабочем листе ячейку или диапазон, на который делается ссылка. Каждое ограничение задачи можно вводить индивидуально. Однако когда знаки ограничений одинаковы, удобнее указывать их левые и правые части в виде диапазонов ячеек. После ввода каждого ограничения, кроме последнего, следует нажимать кнопку Добавить. При этом поля окна Добавление ограничения очищаются и можно вводить следующее ограничение. После ввода последнего из них, щелкните кнопку ОК, чтобы вернуться в окно Поиск решения, где вы увидите список всех введенных ограничений. При необходимости их изменения или удаления можно выделить любое из ограничений и нажать кнопку, соответственно, Изменить или Удалить. 1.2.5 Задание дополнительных параметров поиска решения Чтобы задать другие параметры поиска решения, щелкните кнопку Параметры, открывающую окно Параметры поиска решения (рис. 5),  Рис. 5. Выбор дополнительных параметров поиска решения Значения большинства параметров, установленные по умолчанию, годятся для решения большинства задач. Однако специально для решения задач линейного программирования следует установить два флажка: • Линейная модель — для ускорения поиска решения линейной задачи оптимизации и получения результатов после оптимизационного анализа; • Неотрицательные значения— чтобы переменные были неотрицательны. 1.2.6 Нахождение решения Вернувшись в окно Поиск решения, вы можете приступать к вычислениям. Для этого щелкните кнопку Выполнить. Результаты вычислений появятся на, рабочем листе, и одновременно откроется окно Результаты поиска решения с сообщением о том, найдено решение или нет (рис. 6). 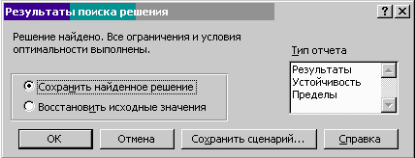 Рис. 6. Сообщение о результатах решения задачи линейного программирования В этом окне можно выбрать следующие параметры: • Сохранить найденное решение — для сохранения найденного решения на рабочем листе. • Восстановить исходные значения — для восстановления исходного вида рабочего листа. • Тип отчета — для выдачи на отдельных рабочих листах отчетов, содержащих анализ полученных результатов. В списке можно выделить один или несколько типов отчета (в случае целочисленного решения доступен лишь один из них— Результаты). Отчет по результатам содержит ту же информацию, что и основной рабочий лист, отчет по пределам не представляет особой ценности, поэтому в дальнейшем подробно анализируется лишь наиболее интересный из отчетов — по устойчивости. В нашей задаче выберите параметр Сохранить найденное решение, выделите в списке тип отчета — Устойчивость и щелкните кнопку ОК. В рабочей книге появится новый лист с этим отчетом. 1.2.7 Анализ результатов Результаты вычислений выглядят на рабочем листе, как показано на рис. 7.  Рис. 7. Результаты решения задачи линейного программирования В ячейках ВЗ:ЕЗ выводится оптимальный производственный план, в ячейке F4 — максимальное значение прибыли. В строках 8-10, содержащих ограничения на ресурсы, в столбце Лев.часть указаны объемы u1080 использованных ресурсов, а в столбце Разница — остаток ресурсов, оставшихся неиспользованными. Если разница равна нулю, то соответствующий ресурс дефицитен (используется полностью), а если разница положительна — то недефицитен (не используется полностью). В строках 9–15, содержащих граничные условия, в столбце Лев.часть указаны значения переменных в оптимальном решении, а в столбце Разница — разность между этими значениями и заданными для переменных верхними и нижними границами. Если разница равна нулю, то соответствующая переменная принимает свое минимальное или максимальное значение. Если, задавая параметры поиска решения, вы установили флажок Линейная модель, то отчет по устойчивости будет содержать сведения о чувствительности решения к изменениям коэффициентов целевой функции и правых частей ограничений (рис. 8).  Рис. 8. Отчет по устойчивости решения задачи линейного программирования В первой из таблиц отчета выводится следующая информация: • В первых двух столбцах перечислены ячейки, в которых вычисляются значения переменных, и их имена. • В столбце Результ. значение— найденное оптимальное решение (5;1,5; 3; 4). • В столбце Нормир. стоимость — двойственные оценки (0; 0; 0; 0). Такая оценка может быть отлична от нуля только для нулевой переменной и показывает, на какую величину в целевой функции следует изменить коэффициент этой переменной, чтобы в оптимальном плане она приняла положительное значение (например, насколько увеличить цену изделия, чтобы его производить стало выгодно). Кроме того, эта оценка показывает, на какую величину ухудшится значение целевой функции, если уйти от оптимального плана, добавив в него единицу соответствующей продукции. • В столбце Целевой Коэффициент — коэффициенты целевой функции. • В последних двух столбцах — допустимые приращения коэффициентов целевой функции, при которых сохраняется прежнее оптимальное решение (при этом 1Е+30 означает 10+30, то есть фактически +∞). При добавлении допустимых приращений к коэффициентам целевой функции получаются интервалы оптимальности. В нашем примере такими интервалами будут: для цены 1-го вида продукции — [30, +∞), для цены 2-го вида продукции — [0,140], для цены 3-го вида продукции — [30, +∞ ) и для цены 4-го вида продукции — [60, +∞). Во второй таблице выводится следующая информация: • В первых двух столбцах перечислены ячейки, в которых вычисляются левые части ограничений, и их имена. • В столбце Результ. значение— значения левых частей ограничений (для ограничений на ресурсы — их использованное количество, для граничных условий — значение переменных в оптимальном плане). • В столбце Теневая Цена — теневые цены— двойственные оценки, показывающие, на какую величину изменится целевая функция при увеличении на единицу правой части ограничения или граничного условия, тогда как остальные данные неизменны (в частности при добавлении единицы соответствующего ресурса). Теневая цена — это максимальная цена, которую стоит платить за дополнительное количество дефицитного ресурса, чтобы его приобретение было выгодным. • В столбце Ограничение Правая часть — правые части ограничений (запасы ресурсов или граничные значения переменных). • В последних двух столбцах — допустимые приращения правых частей ограничений (запасов ресурсов или граничных значений переменных), при которых неизменны соответствующие теневые цены и в оптимальном решении сохраняется прежний набор ненулевых переменных (ассортимент продукции). При добавлении допустимых приращений к правым частям ограничений получаются интервалы устойчивости. В нашем примере такими интервалами будут: для трудовых ресурсов— [18,20,6], для сырья— [72,+∞) и для финансов — [94,5, +∞) После анализа результатов, можно изменить исходные данные на рабочем листе и повторить вычисления. При этом не понадобится повторно вводить ограничения или изменять параметры решения: достаточно лишь выбрать в меню Сервис команду Поиск решения и в открывшемся окне нажать кнопку Выполнить. Вся информация, заданная в окне Поиск решения, постоянно хранится вмести с рабочим листом, к которому она относится. Не пропадет эта информация и при сохранении рабочей книги на диске. |
