Лабораторная работа. Лабораторная работа 3(523B) изучение явлений, обусловленных дифракцией
 Скачать 191.5 Kb.
|
|
ЛАБОРАТОРНАЯ РАБОТА № 3(523B) ИЗУЧЕНИЕ ЯВЛЕНИЙ, ОБУСЛОВЛЕННЫХ ДИФРАКЦИЕЙ Цель работы: наблюдение дифракции света на дифракционной решетке, определение длины волны света и периода дифракционной решетки. Оборудование: дифракционная решетка, щель, оптическая скамья, источники света (ртутная лампа, лампа накаливания). Теоретические сведения. Дифракцией называется явление огибания волнами препятствий. Применительно к световым волнам дифракция означает проникновение света в область геометрической тени. Одним из наиболее распространенных технических средств для создания дифракционных эффектов служит дифракционная решетка. Дифракционной решеткой называется тонкая структура, содержащая ряд параллельных равноотстоящих и близко расположенных друг от друга щелей. Расстояние d между серединами соседних щелей или сумма прозрачной а и непрозрачной b частей называется постоянной дифракционной решетки d=a+b (рис.1). П 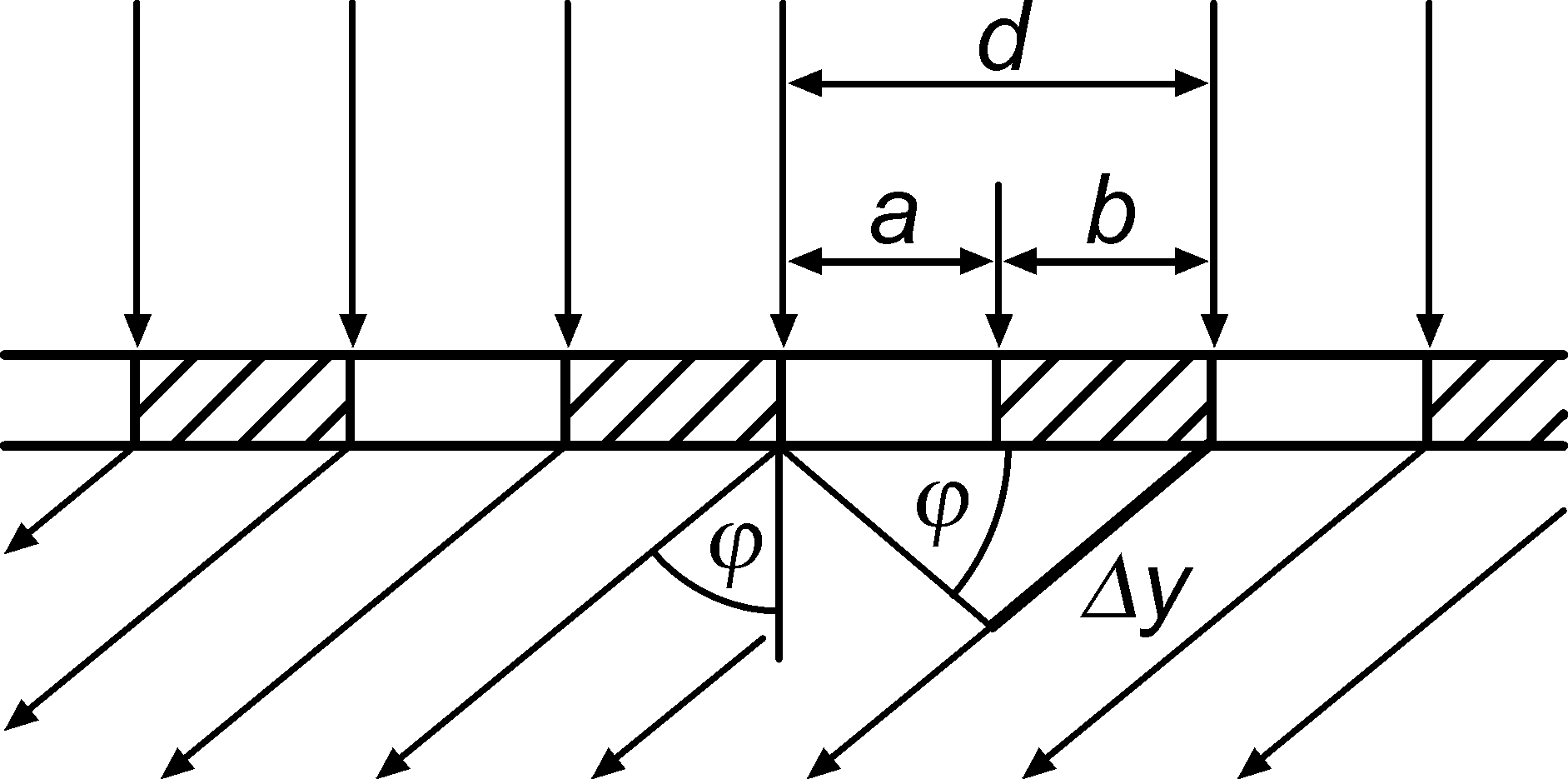 Рис. 1 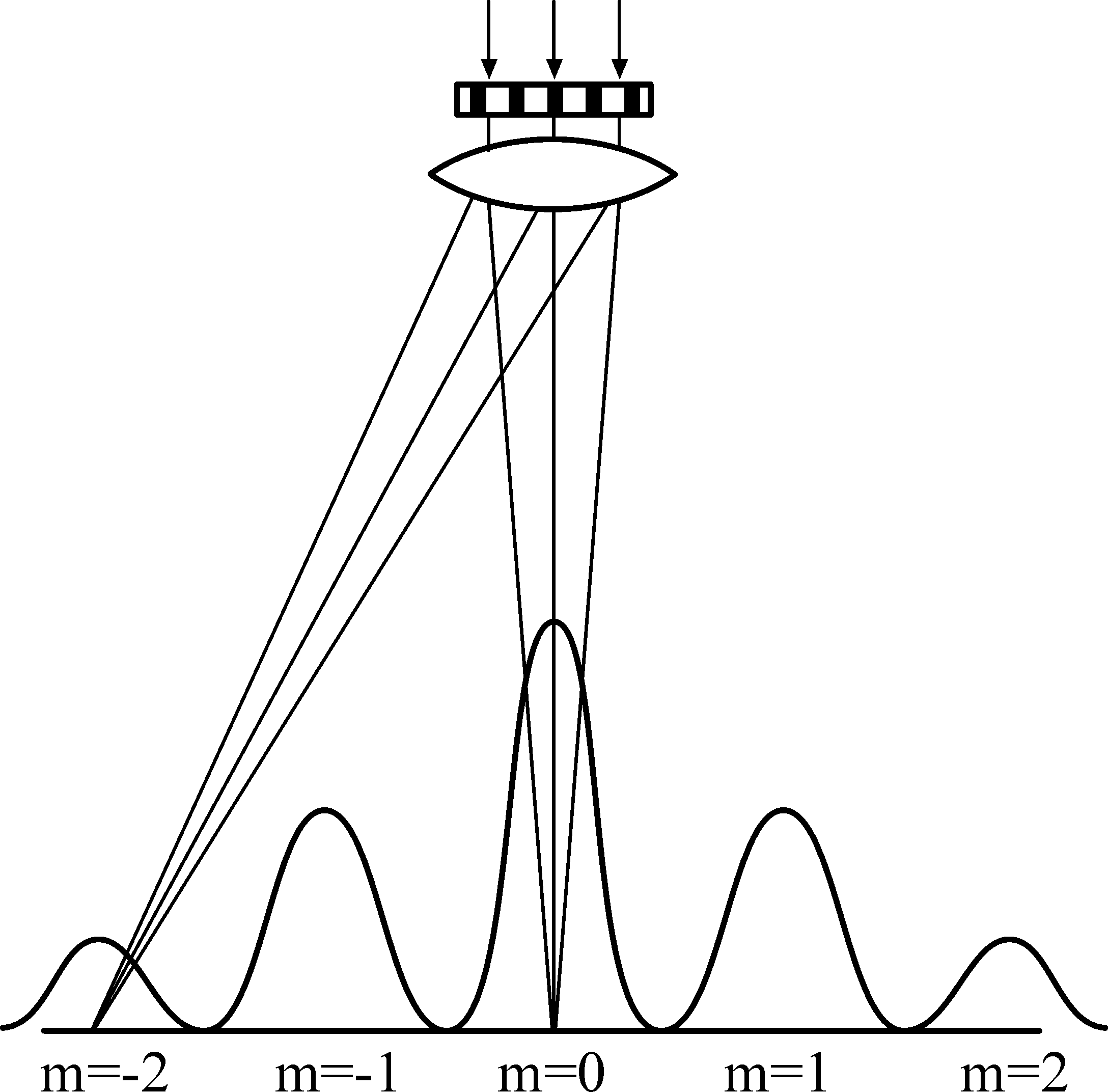 Рис. 2 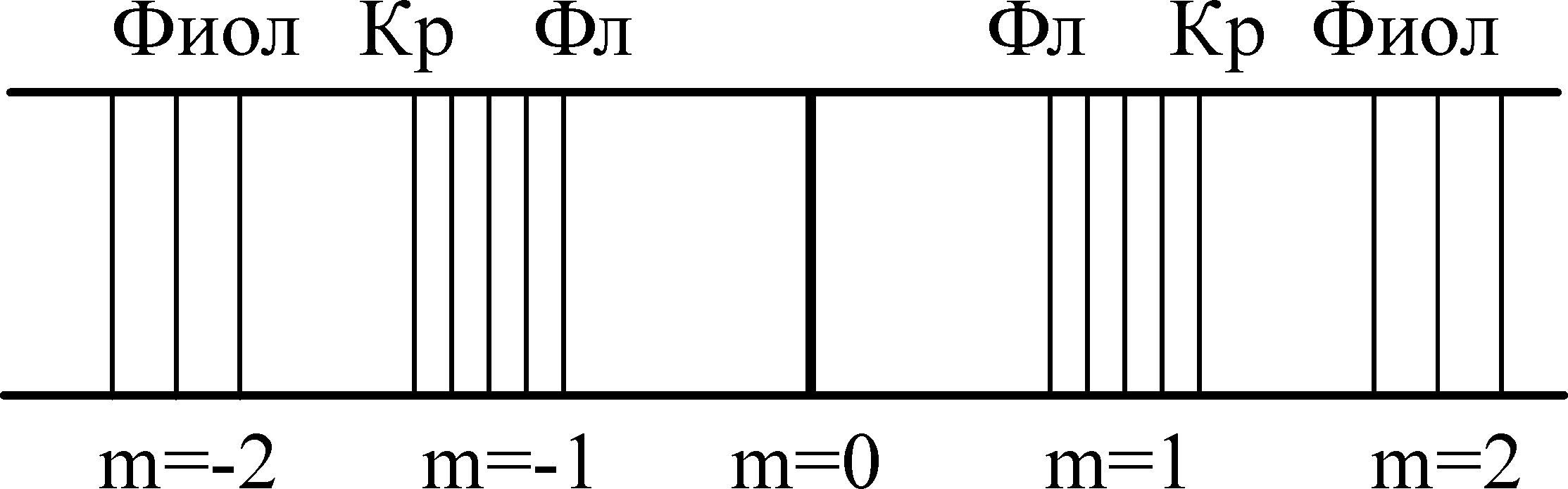 Рис. 3 ри падении плоской световой волны на решетку каждый элемент её поверхности становится источником вторичных когерентных волн. Результирующее световое колебание в любой точке пространства определяется согласно принципу Гюйгенса-Френеля суммированием вторичных волн, приходящих в данную точку от всех элементов решетки, с учетом их амплитуд и фаз. Если на пути волн за решеткой поставить собирающую линзу, то в плоскости будет наблюдаться дифракционная картина (рис.2). Дифракционную картину можно наблюдать непосредственно глазом, воспринимая лучи, прошедшие сквозь решетку. Роль линзы в этом случае играет хрусталик глаза. Главные дифракционные максимумы возникают в тех направлениях, для которых оптическая разность хода лучей, идущих от соседних щелей решетки, равна целому числу длин волн : y=m Из рис.1 видно, что оптическая разность хода лучей, идущих от двух соседних щелей под углом дифракции, y=dsin (1). Таким образом, углы дифракции, под которыми наблюдаются максимумы, определяются условием dsin=m (2). Здесь m=0,1,2…- порядок дифракционного максимума. Из формулы (2) следует, что если падающий свет содержит несколько различных длин волн, то решетка разложит его в спектр (рис.3). В направлении начального распространения света (=0) возникает максимум нулевого порядка (m=0). Справа и слева от него возникнут сплошные или линейчатые спектры различных порядков (m=1,2…). В каждом из спектров максимумы более коротких длин волн располагаются ближе к центральной полосе. Угловой дисперсией спектрального прибора D называют величину D=  ,где d - угловое расстояние между близкими спектральными линиями, d - разность длин волн этих спектральных линий.Для нахождения конкретного вида выражения D продифференцируем уравнение (2). Тогда получим D=  ,г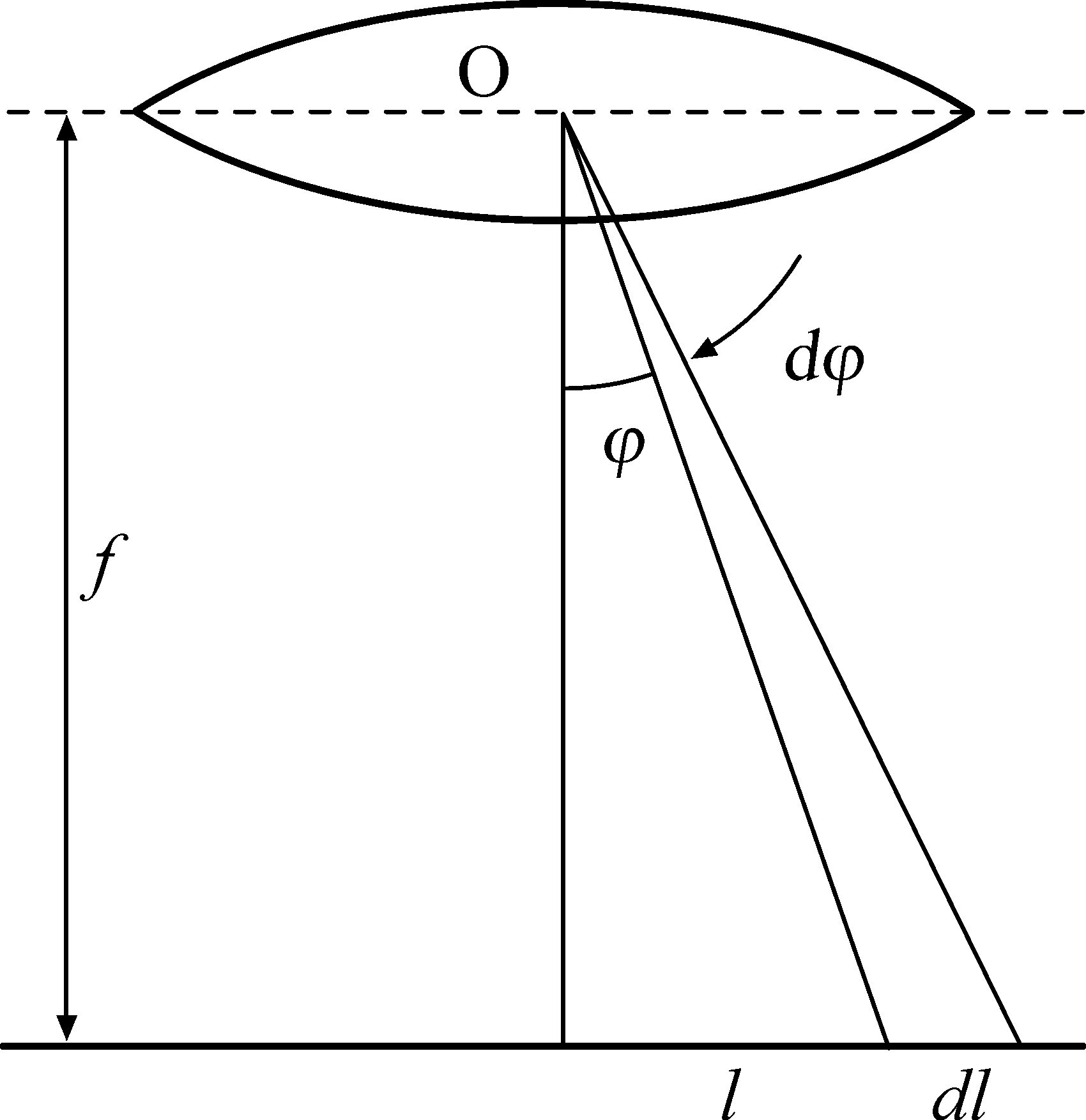де m - максимальный порядок спектра, который можно получить с помощью решётки, d - период решетки, - угол между нормалью и направлением на m – й порядок спектра (Для малых: D = m/d).Л  Рис. 4 инейной дисперсией называют величину, численно равную отношению расстояния dl на экране (или фотопластинке) между близкими спектральными линиями к разности d длин волн этих спектральных линий Dl=  Из рис.4 следует, что при малых отрезок dl=fd, где f - главное фокусное расстояние линзы. Тогда Dl=  =fDОписание установки Оптическая схема установки показана на рис.5. Все элементы установки помещаются в стойках на оптической скамье. С 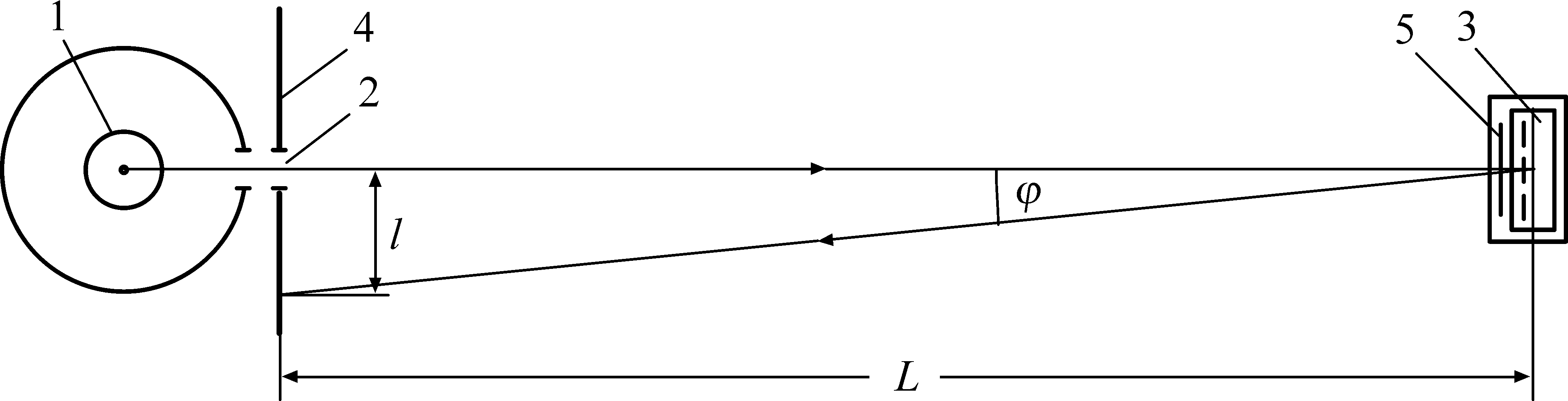 Рис. 5 вет от источника I, пройдя через щель 2, попадает на дифракционную решетку 3. Дифракционная картина наблюдается непосредственно глазом на экране 4. Максимум нулевого порядка (центральный) совпадает со щелью. По обе стороны от нее расположены главные максимумы первого, второго и т.д. порядков. На экране находится отсчетная линейка. Из рис.5 видно, что sin=  (3), где L - расстояние от экрана до дифракционной решетки; l - расстояние от щели до максимума с углом дифракции . Подставляя значение синуса в уравнение (2), получаем  (4)Задание 1. Исследование линейчатого спектра (определение постоянной дифракционной решетки) 1. На оптическую скамью (рис. 5) устанавливаем ртутную лампу 1, дающую линейчатый спектр, экран 4 со щелью 2 и дифракционную решетку 3 . 2. Подключив ртутную лампу к «Блоку питания ламп» в разъём «Ртутная лампа», включаем ртутную лампу и, перемещая щель или дифракционную решетку в вертикальном направлении, добиваемся попадания светового луча на дифракционную решетку. ВНИМАНИЕ. Если после включения клавиши выключателя ртутная лампа не загорится, немедленно выключить блок питания, дать лампе остыть и, затем, повторно включить ртутную лампу. 3. Наблюдаем через дифракционную решетку на экране со шкалой дифракционную картину в виде линейчатых спектров. Регулируя расстояние между решеткой и щелью, получаем четкое изображение спектров 1 и 2 порядков. 4. Измеряем расстояние между дифракционной решеткой и экраном. 5. По шкале влево l' и вправо l" от центрального максимума определяем положение первой фиолетовой линии в спектре 1 и 2 порядка, и результаты записываем в табл. 1. 6. Аналогичные измерения проводим для других ярких линий спектра ртути, и результаты заносим в ту же таблицу. 7. По полученным данным для каждой линии спектра рассчитываем её среднее расстояние  от центрального максимума и постоянную дифракционной решетки по формуле (4). Находим среднее значение величины  .8. Рассчитываем доверительный интервал d . Записываем окончательный результат и сделаем выводы. Задание 2. Исследование светофильтра (определение области, прозрачности светофильтра в видимой части спектра с помощью дифракционной решетки). Часть сплошного спектра, для которой данный фильтр прозрачен" называется областью прозрачности светофильтра или полосой пропускания светофильтра. Цель данного упражнения - определить область прозрачности фильтра. Для этого надо найти коротковолновую к и длинноволновую д границу области прозрачности фильтра. Область прозрачности находится между к и д Таблица 1
1. На оптическую скамью (рис. 5) устанавливаем лампу накаливания 1, дающую сплошной спектр, экран 4 со щелью 2и дифракционную решетку 3. Постоянная решетки указана на ее корпусе. 2. Подключив галогеновую лампу к «Блоку питания ламп» в разъём «Галогеновая лампа», включаем галогеновую лампу и, перемещая щель или дифракционную решетку вертикальном направлении, добиваемся попадания светового луча на дифракционную решетку. 3. Наблюдаем через дифракционную решетку на экране со шкалой 4 дифракционную картину в виде сплошных спектров. Регулируя расстояние между дифракционной решеткой и щелью, получаем четкое изображение спектров 1 и 2 порядков. 4. Устанавливаем исследуемый светофильтр 5 (рис. 5) и записываем его цвет в табл. 2. 5. Измеряем расстояние L между дифракционной решеткой к экраном. 6. Наблюдаем спектры первого порядка. По шкале слева  и справа  от центрального максимума определяем положение коротковолновой границы пропускаемого светофильтром света (рис. 6) с точностью до 1 мм. Результаты измерения заносим в табл. 2.Таблица 2
7. Находим среднее значение lк и по формуле (4) рассчитаем коротковолновую к границу спектра. 8. Аналогичные измерения и расчеты проводим для спектра второго порядка. Из двух полученных значений к до 1 и 2 порядку спектра берем среднее. Это и будет окончательным значением коротковолновой границей пропускаемого светофильтром света. 9 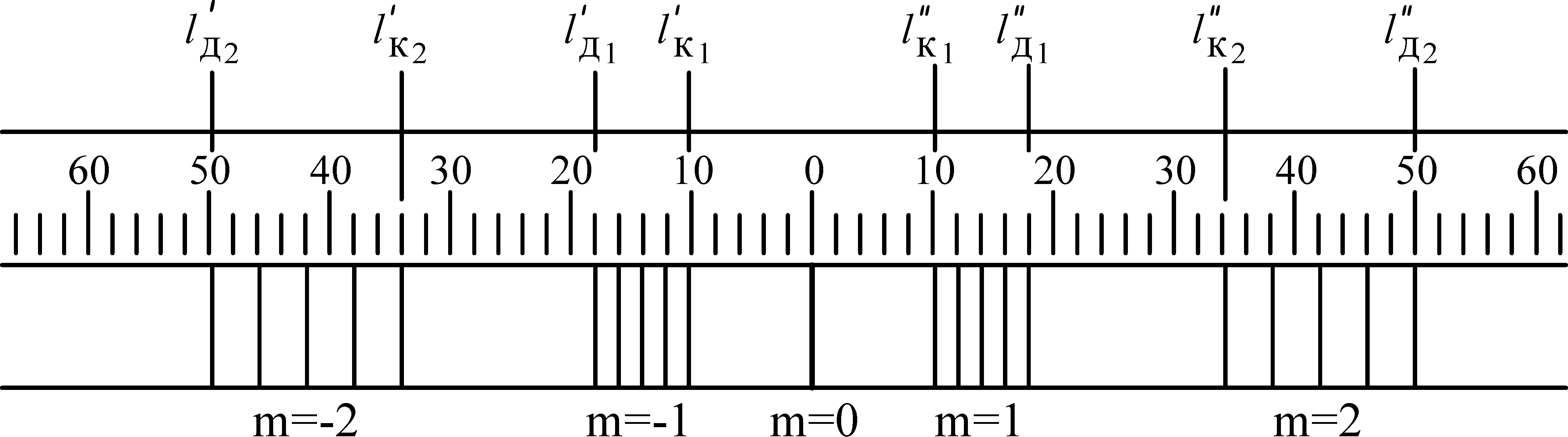 Рис. 6 . Повторяем пункты 6-8 для нахождения длинноволновой границы пропускаемого светофильтром света. Результаты измерений и расчетов заносим также в табл.2. 10. Делаем выводы. 11. Аналогичные измерения и расчеты по пп. 6-10 проводим для других светофильтров. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
,
м
м2
