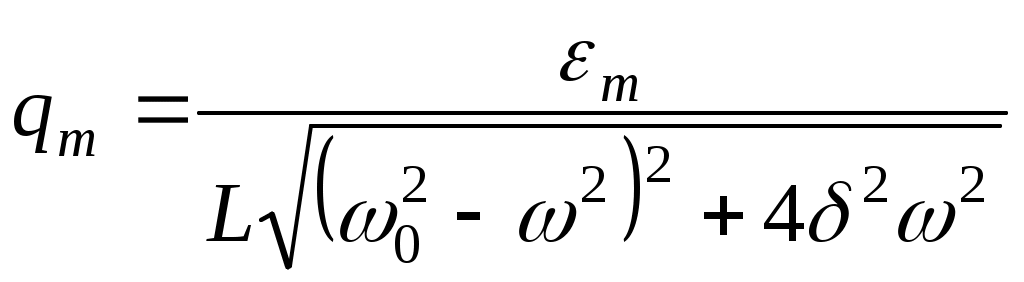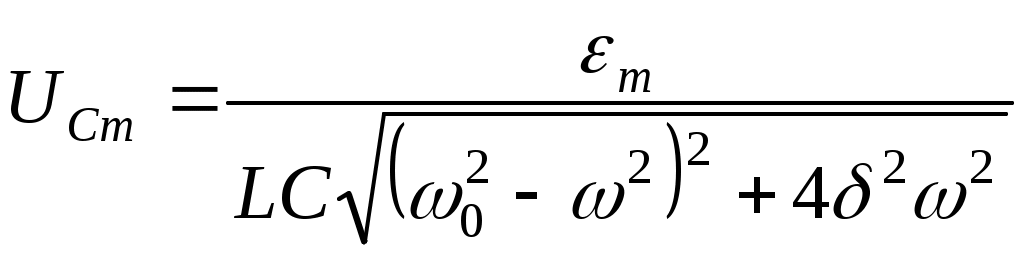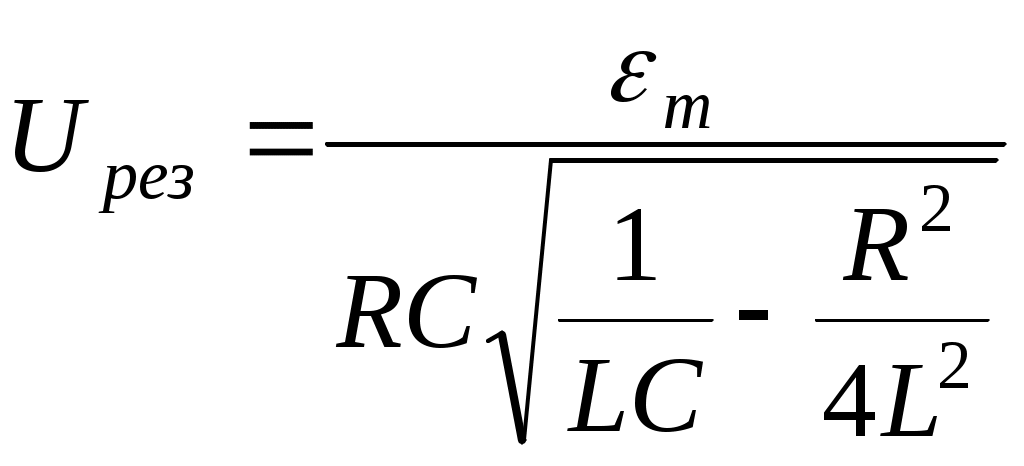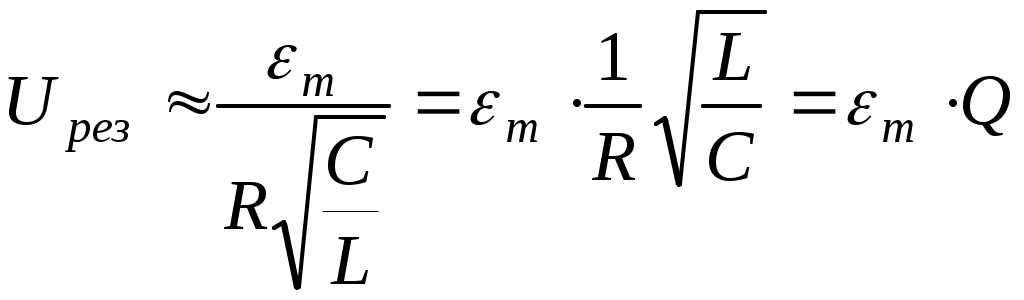лаьба. 36 лаба. Лабораторная работа 36 Изучение вынужденных электрических колебаний Цель работы
 Скачать 5.05 Mb.
|
|
Лабораторная работа № 36 Изучение вынужденных электрических колебаний Цель работы:Исследование изменений амплитуды вынужденных колебаний в электромагнитном колебательном контуре в зависимости от частоты переменного напряжения, приложенного к контуру, а также параметров контура: сопротивления, индуктивности, емкости. Приборы и принадлежности В состав лабораторной установки входит: Осциллограф С1-83 (или С1-93). Генератор сигналов низкочастотный Г-112. Панель «Затухающие электрические колебания. Резонанс». Соединительные провода. 1. Теоретическое введение Процессы, возникающие в электрических цепях под действием источника тока с периодически изменяющимся напряжением, называются вынужденными колебаниями. Вынужденные колебания, в отличие от собственных колебаний в электрических цепях, являются незатухающими. Внешний источник обеспечивает приток энергии к системе, компенсируя тем самым ее неизбежные потери. Особый интерес представляет случай, когда внешний источник, напряжение которого изменяется по гармоническому закону с частотой ω, включен в электрический контур, в котором возможны собственные свободные колебания напряжения с частотой ω0. Частота установившихся вынужденных колебаний всегда равна частоте ω внешнего источника, тогда как частота ω0 свободных колебаний определяется параметрами электрической цепи. Электрические цепи, в которых происходят установившиеся вынужденные колебания под действием периодического внешнего напряжения, называются цепями переменного тока.
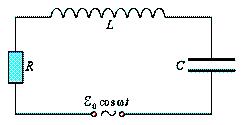
где  0 – амплитуда, ω – круговая частота.Предполагается, что для электрической цепи, изображенной на рис. 1, выполнено условие квазистационарности. Поэтому закон Ома можно записать для мгновенных значений токов и напряжений:
В общем случае получим дифференциальное уравнение колебаний заряда q(t) в RLC - контуре при действии внешней ЭДС в виде:
Используя обозначения  и  , приводим уравнение (2) к виду:
Решение данного неоднородного дифференциального уравнения показывает, что при установившихся вынужденных колебаниях заряд конденсатора изменяется гармонически с частотой ω, а его амплитуда qm и начальная фаза φ0 находятся по формулам:
Амплитуда напряжения на конденсаторе  , следовательно
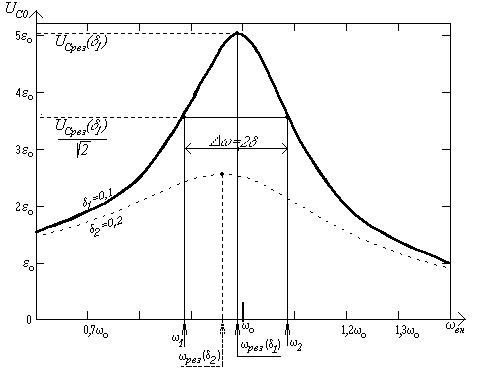
Графики зависимости  называются резонансными кривыми колебательного контура, которые представлены на рис. 2. Достижение амплитудой  вынужденных колебаний напряжения своего максимального значения при некоторой частоте внешней ЭДС называется резонансом (резонансом напряжения).Частота  колебаний внешней ЭДС, при которой амплитуда вынужденных колебаний достигает максимума, называется резонансной частотой. Ее значение можно найти, исследуя функцию (5) на экстремум, то есть, приравняв к нулю производную  и решив полученное уравнение относительно частоты. В итоге получим, что резонансная частота равна:
Соответствующее максимальное (резонансное) значение амплитуды вынужденных колебаний напряжения получим, подставляя выражение (6) в уравнение (5) и упрощая полученное выражение:
При резонансе резко возрастают напряжения на конденсаторе и катушке индуктивности. Эти напряжения становятся одинаковыми и во много раз превосходят внешнее напряжение. Вследствие явления электрического резонанса контур сильнее всего реагирует на ЭДС, частота которой равна или близка к резонансной частоте контура. На этом явлении основаны все радиоприемные устройства, неотъемлемой частью которых является колебательный контур, резонансная частота которого может изменяться путем изменения его емкости или индуктивности
 будет тем слабее, чем «острее» резонансная кривая для контура, то есть чем «резче» зависимость напряжения на конденсаторе от частоты. «Остроту» резонансной кривой можно охарактеризовать с помощью относительной ширины этой кривой, равной  , где  - разность значений  и  циклических частот, при которых амплитуда вынужденных колебаний в  раз меньше резонансной амплитуды (рис.2). Можно показать, что разность этих частот, называемая шириной резонансной кривой, при малом затухании, при котором выполняется условие R  или  , равна  . Это свойство позволяет определить коэффициент затухания  как полуширину резонансной кривой:
Для характеристики затухания колебаний в контуре вводится величина, называемая добротностью. Добротностьюколебательной системы называется безразмерная физическая величина, равная произведению 2π на отношение энергии, подведенной к контуру, к потере энергии в контуре ΔWза один период колебаний Т:  Добротность электрического колебательного контура определяется как отношение волнового сопротивления контура к его электрическому сопротивлению:
Можно показать, что при малом затухании относительная ширина резонансной кривой есть величина, обратная добротности контура:
Формула (7) при малом затухании преобразуется к виду
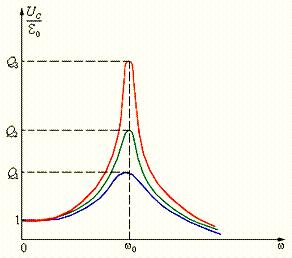
Таким образом, при резонансе амплитуды напряжений на конденсаторе и катушке в Q раз превышают амплитуду напряжения внешнего источника. Рис. 3 иллюстрирует явление резонанса в последовательном электрическом контуре. На рисунке графически изображена зависимость отношения амплитуды UC напряжения на конденсаторе к амплитуде 0 напряжения источника от его частоты ω для различных значений добротности Q. Кривые на рис. 3 называются резонансными кривыми.
Можно показать, что максимум резонансных кривых для контуров с низкой добротностью несколько сдвинуты в область низких частот относительно собственной частоты контура. «Острота» резонансной кривой сильно зависит от энергетических потерь в контуре. При увеличении активного сопротивления контура резонансная кривая становится менее «острой». 2. Описание установкиУ  становка представляет собой панель, в которой последовательно соединены катушка L, конденсатор С и резистор R. Конструкция панели предоставляет возможность включать в цепь резисторы и конденсаторы с разными параметрами. Переменное напряжение синусоидальной формы подается от низкочастотного генератора Г-112 с частотой от 30 до 100 кГц. Для исследования амплитуды вынужденных колебаний напряжение с конденсатора подается на вертикально отклоняющие пластины осциллографа. Вследствие синхронизации напряжения, задаваемого генератором и частоты развертки осциллографа, на экране осциллографа можно добиться неподвижной картины временной зависимости напряжения вынужденных колебаний.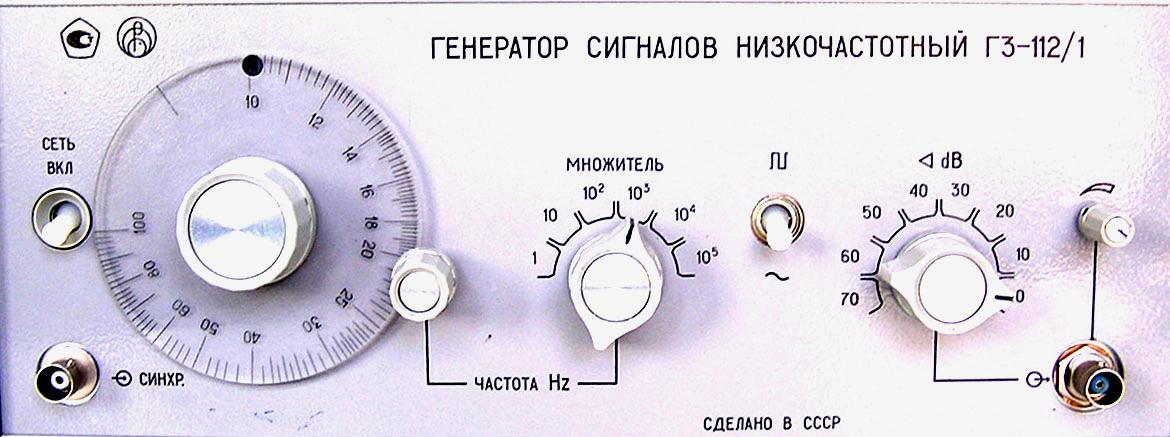            Рис. 5. Генератор сигналов низкочастотный (передняя панель):. 1 – тумблер включения питания; 2 – неоновая лампа-указатель частоты; 3 – ручка плавной регулировки частоты; 4 – переключатель «множитель» для ступенчатого переключения частоты; 5 – тумблер переключения формы сигнала; 6 – переключатель ступенчатого ослабления сигнала; 7 – гнездо «выход» для вывода сигнала во внешнюю цепь; 8 – ручка плавного изменения амплитуды сигнала.  Рис. 6. Осциллограф двухканальный С1-93 (передняя панель). 1 – гнездо «вход» канала II; 2 – ручка плавного изменения чувствительности (в норме повернута против часовой стрелки до упора); 3 – ручка ступенчатого переключения чувствительности; 4 – ручка включения-выключения развертки по оси «Y» канала II; 5 – гнездо «вход» канала I; 6 – ручка плавного изменения чувствительности канала I; 7 – ручка ступенчатого переключения чувствительности канала I; 8 – ручка включения-выключения развертки по оси «Y» канала I; 9 – кнопки переключения каналов; 10 – ручка перемещения электронного луча по оси «Y»; 11 – ручка перемещения электронного луча по оси «Х»; 12 – ручка ступенчатого изменения цены деления (чувствительности) развертки по времени; 13 – ручка плавного изменения чувствительности развертки по времени (в норме повернута против часовой стрелки до упора); 14 – кнопки управления синхронизацией; 15 – ручка включения-выключения питания; 16 – ручка управления фокусировкой электронного луча; 17 – ручка управления яркостью электронного луча; 18 – ручка перемещения электронного луча по оси «Y». 3. Порядок выполнения работыС помощью соединительных проводов подключить «выход» генератора (7) на рис. 5 и «вход» осциллографа (1) на рис. 6 к панели «Затухающие электрические колебания. Резонанс» согласно указателям на панели. На панели с помощью соединительных проводов установить заданные преподавателем значения сопротивления R и емкости конденсатора С. На панелях генератора и осциллографа ручки и переключатели установить в положение: на панели генератора (рис.5) - частота (2) 20-50 - множитель (4) 103 - переключатель (5) вниз - переключатель (6) в положение 0 на панели осциллографа (рис. 6): - кнопку (9) нажать «II» - ручку (2) по часовой стрелке до упора - ручку (3) в положение «1 В/дел» - ручку (4) в верхнее или нижнее положение - ручку (12) (ВРЕМЯ/ДЕЛ) в положение 5 µs или 10 µs (микросекунд) - убедиться что ручка (13) повернута по часовой стрелке до упора - кнопку (14) нажать в положении «внутр II» 3. Включить генератор тумблером (1) (рис. 5) и осциллограф ручкой (15) (рис. 6), предварительно убедившись, что шнуры питания включены в сеть 220 В. 4. Поворачивая ручку усиления (8) генератора (рис. 5) получить осциллограмму напряжения вынужденных колебаний. Ручками (11) и (18) переместить осциллограмму так, чтобы она располагалась симметрично относительно оси Х и начиналась у левого края экрана. Задание 1. Определение резонансной частоты и амплитуды вынужденных колебаний. Плавно вращая ручку (3) генератора (рис.5), добейтесь максимальной амплитуды сигнала, то есть резонанса, при необходимости регулируя ее ручкой (8) так, чтобы осциллограмма не выходила за пределы экрана. Убедитесь, что синусоида симметрична относительно оси Х. По горизонтальной шкале экрана осциллографа измерьте продолжительность t нескольких (N) полных колебаний. Цена большого деления шкалы задаётся ручкой (12) «ВРЕМЯ/ДЕЛ» в миллисекундах (ms) или микросекундах (µs). Для более точного измерения времени можно изменить цену деления ручкой множителя «х1- х0,2», выдвинув её на себя. При этом цена деления шкалы времени уменьшается в 5 раз. Для удобства и повышения точности измерения ручкой (11) осциллографа можно переместить осциллограмму вдоль оси Х так, чтобы начало измеряемых колебаний находилось в точке пересечения одной из крайних вертикальных линий шкалы экрана с осью Х. Определите период колебания по формуле Трез= t/N и резонансную частоту νрез = 1/Трез. Полученное значение может несколько отличаться от показаний шкалы генератора вследствие смещения шкалы. Оцените величину этой систематической погрешности определения частоты колебаний. Измерьте амплитуду Арез колебаний по вертикальной шкале экрана. Результаты измерений и вычислений занесите в табл. 1. Задание 2. Получение резонансных кривых. Вращая ручку (3) генератора, уменьшите частоту подаваемого напряжения на 15-20 кГц (7-10 делений) так, чтобы амплитуда сигнала уменьшилась примерно в 2 раза. По вертикальной шкале экрана осциллографа измерьте амплитуду А сигнала (в делениях шкалы). Соответствующие значения частоты ν и амплитуды А запишите в табл. 1. Повторите измерения 15-20 раз, увеличивая частоту с помощью ручки (3) генератора через 2 кГц до тех пор пока амплитуда сигнала пройдя наибольшее значение снова не уменьшится примерно в 2 раза по сравнению с Арез Изменив один из параметров контура (индуктивность, емкость или сопротивление) по указанию преподавателя, выполните действия, указанные в пп 5 – 11. Результаты измерений амплитуды при различных частотах и параметрах занесите в табл. 1. По данным табл. 1 постройте на миллиметровой бумаге графики зависимости амплитуды вынужденных колебаний от частоты генератора (резонансные кривые). Примечание: - при выборе масштаба графика отсчет по оси Х (частота) начинается не нуля, а с самого малого измеренного значения частоты; - резонансная частота, как правило, не совпадает с показаниями шкалы, поэтому значение максимальной амплитуды при построении графика возьмите из п.8. Задание 3. Исследование резонансных кривых и определение характеристик колебательного контура. Вычислите собственную частоту колебательного контура в каждой серии измерений по формуле  и сравните ее с измеренным значением резонансной частоты νрез.Сравните измеренное значение резонансной частоты с расчетным (теоретическим) значением резонансной частотой, которое определяется по формуле: 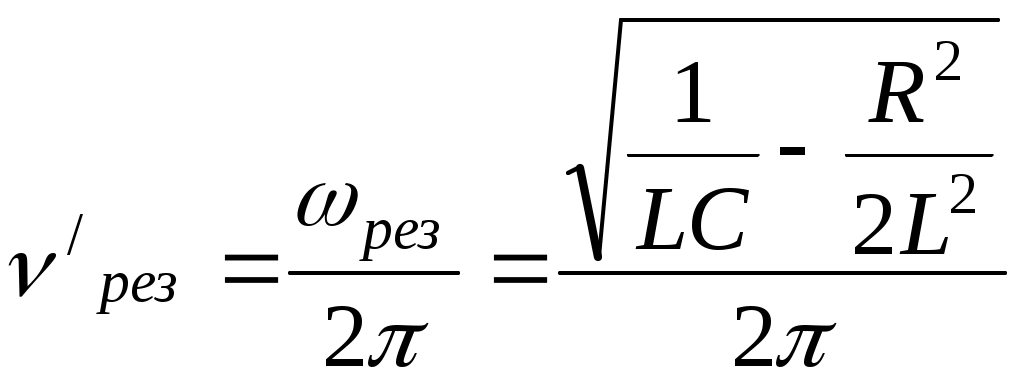  По графику определите ширину резонансной кривой. Для этого вычислите значение амплитуды А1/2, соответствующей половине максимальной мощности вынужденных колебаний, или в  раз меньше максимальной (резонансной) амплитуды, т.е  . Затем проведите прямую параллельную оси частот, которая пересечет резонансную кривую при двух частотах ν1 и ν2. Ширину резонансной кривой определите как  или как отрезок прямой между точками пересечения с резонансной кривой (в соответствующем масштабе).Определите экспериментальные значения добротности контура Qэксп и коэффициента затухания δэксп по формулам:  и  и сравните их с теоретическими значениями добротности Qmeop и коэффициента затухания δтеор, которые рассчитываются по формулам:  и  Результаты измерений и вычислений занесите в таблицу 2. Таблица 1
Таблица 2
Контрольные вопросы: Какой процесс называется колебательным. Какие бывают колебания. Какие колебания называются гармоническими, по какому закону они совершаются. Какими параметрами описываются колебания. Дать определение амплитуды, частоты, периода. Что представляют собой электромагнитные колебания. Что называется резонансом, как он проявляется. Колебательный контур, процессы происходящие в нём. Формула Томсона. Как определить собственную частоту колебательного контура. Какому условию должна удовлетворять частота вынуждающей силы при резонансе. Что называется добротностью контура колебательной системы. От чего она зависит. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
или 
, кГц
с-1
с-1