Лаба По Физике. Лабораторная работа 36 к определение магнитного момента полосового магнита Казань 2002
 Скачать 226 Kb. Скачать 226 Kb.
|
|
Министерство образования Российской Федерации КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ имени А.Н. Туполева Кафедра общей физики Лабораторная работа № 36 КОпределение магнитного момента полосового магнита Казань 2002 Измерение магнитного момента полосового постоянного магнита при использовании компаса, линейки и секундомера. Цель работы: Измерение магнитного момента полосового постоянного магнита. Приборы и принадлежности. Полосовой постоянный магнит, компас, секундомер, линейка, тонкая нить с обоймой для закрепления ее на полосовом магните. 1.Магнитное поле и его силовая характеристика. Закон Ампера Магнитное поле возбуждается движением электрических зарядов, то есть электрическими токами. Силовой характеристикой магнитного поля является вектор магнитной индукции B. В произвольной точке магнитного поля вектор B по направлению совпадает с направлением северного полюса бесконечно маленькой магнитной стрелки, имеющей возможность вращаться вокруг оси без трения. Модуль вектора В можно определить по закону Ампера dF=I·dl·B·sin , (1.1) где dF – сила, действующая на элемент проводника длиной dl, по которому протекает ток I, – угол между векторами dl и B. Из этого уравнения найдем индукцию магнитного поля при =/2 Единица магнитной индукции – тесла (Тл).Найдем размерность магнитной индукции из уравнения (1.2): [B]=MT-2I-1. 2. Контур с током, полосовой постоянный магнит и стрелка компаса в магнитном поле. Пусть плоский контур с током помещается в однородное магнитное поле с индукцией B. По правилу буравчика выберем направление нормали n к плоскости контура (с конца вектора n ток I виден протекающим против часовой стрелки). Модуль единичного вектора n равен 1. При совпадении направлений векторов B и n (угол между ними равен нулю) на контур вращающий момент М не действует. При возрастании угла возрастает вращающий момент, стремящийся уменьшить угол.. Опыты показали, что независимо от формы контура этот момент пропорционален модулю вектора B, произведению тока I в контуре, площади контура S и sin. Поэтому можно записать М = – B·I·S·sin . Величину pm = I·S (2.1). называют магнитным моментом контура. Магнитный момент – величина векторная. Он по направлению совпадает с вектором n. Следовательно, из этих уравнений получим pm=ISn, (2.2) М = –B·pm·sin(2.3) M= - [B,pm] = [B, pmn]. (2.4) Магнитное поле полосового магнита и стрелки компаса определяется очень большим количеством круговых микротоков, нормали n к которым ориентированы параллельно друг к другу. Поэтому и для полосового постоянного магнита, и для стрелки компаса можно пользоваться уравнениями (2.3) и (2.4), В соответствии с ними стрелка компаса при отсутствии трения в опоре устанавливается вдоль магнитного меридиана Земли, а плоскость рамки с током стремится установиться перпендикулярно вектору B. 3..Закон Био-Савара-Лапласа. Индукция магнитного поля в центре кругового тока. По закону Био-Савара-Лапласа каждый элементарный участок тока длины dl, направленный в ту сторону, в которую течет ток, создает магнитное поле, индукция dB которого в любой точке поля определяется формулой (3.1) где 0 магнитная постоянная ( 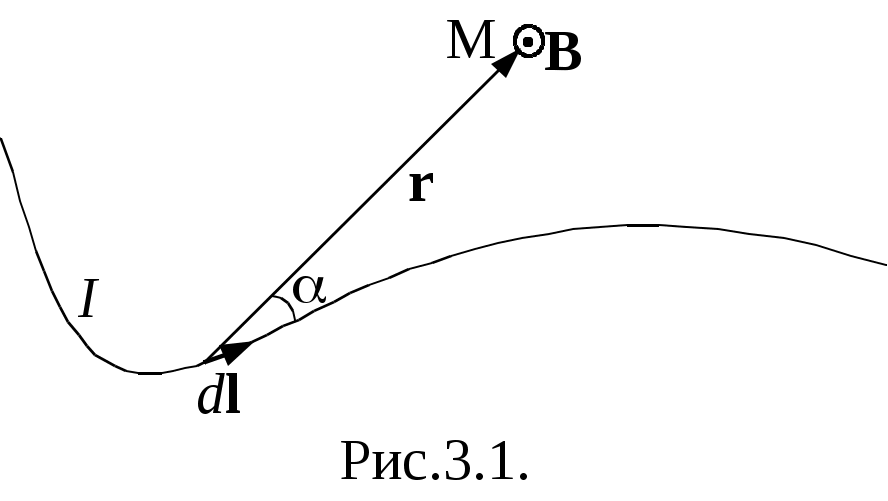 Вектор dB перпендикулярен плоскости, в которой лежат векторы dl и rи направлен так, что с конца вектора dB поворот вектора dl до совмещения с вектором r по кратчайшему пути виден происходящим против часовой стрелки. Из уравнения (3.1) следует где – угол между векторами dlи r. На рис.3.1 изображены проводник произвольной формы с током и вектор В индукции магнитного поля образованного элементом dl проводника в точке М пространства. Обозначение точки в центре круга означает, что вектор выходит из-за плоскости чертежа. Для нахождения индукции магнитного поля в точке пространства, созданного током всего проводника, необходимо проинтегрировать выражение (3.2) по всей длине проводника. При этом могут меняться величина радиус-вектора и угол . 4. Индукция магнитного поля на оси кругового тока и полосового постоянного магнита. Предварительно найдем индукцию B1 на оси кругового тока на расстоянии x от плоскости, в которой лежит контур (рис. 4.1) 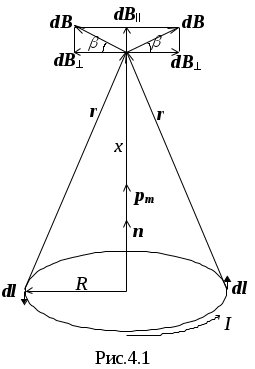 Вектор dB определяем по закону Био-Савара-Лапласа (3.1), а его модуль – по уравнению (3.2). Так как векторы dl и r взаимно перпендикулярны, то sin в уравнении (3.2) равен 1. Из рис. 4.1 r2 = R2+x2. Тогда из уравнения (4.1) получим Из уравнения (4.2) видно, что векторы dB по модулю равны между собой при равных по длине элементах dl. Поэтому равны все векторы dB, расположенные в плоскости, перпендикулярной оси x, а векторная сумма всех векторов dB равна нулю. Все векторы dB||, расположенные по оси x, направлены одинаково и равны между собой. Поэтому Из уравнения (4.2) и двух последних уравнений получим: 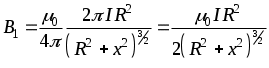 . (4.3) . (4.3)Площадь S1, охватываемая контуром с током, равна.S = R2. Поэтому, с учетом (2.1), можно из (4.3) получить 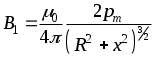 . (4.4) . (4.4)Единичная нормаль n к плоскости кругового тока I направлена по правилу буравчика (с конца вектора n ток I виден протекающим против часовой стрелки). Векторы B1, pm, n направлены одинаково. Из (4.4) получим 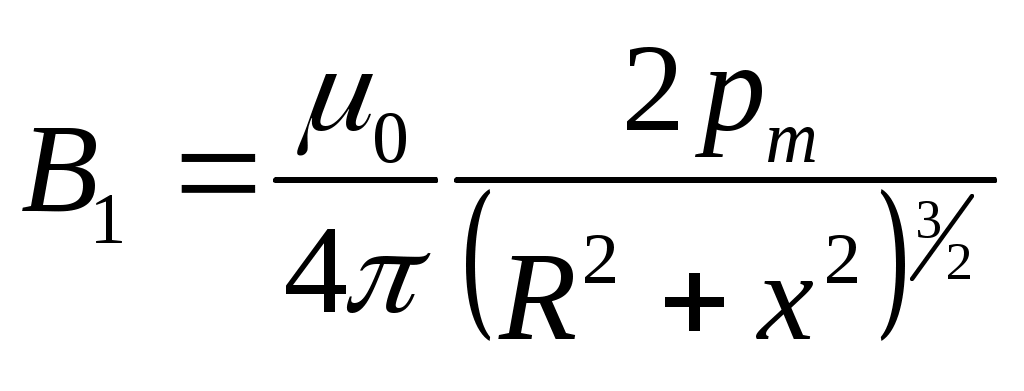 . (4.5) . (4.5)При x>>R можно пренебречь радиусом кругового тока R: Магнитное поле полосового магнита определяется очень большим количеством круговых микротоков, нормали n к которым параллельны друг к другу. Поэтому для магнита также можно пользоваться уравнением (4.6), если x3a, где a – длина магнита, а x – расстояние вдоль оси магнита, отсчитываемое от центра магнита. 4. Принцип суперпозиции магнитных полей и измерениегоризонтальной составляющей индукции магнитного поля Земли Земля является большим постоянным магнитом. Индукция магнитного поля Земли на экваторе направлена горизонтально, а на магнитных полюсах – вертикально поверхности Земли. В других точках Земли, в том числе в Казани, она наклонена к горизонту. Обозначим через B0 вектор горизонтальной составляющей магнитного поля Земли. 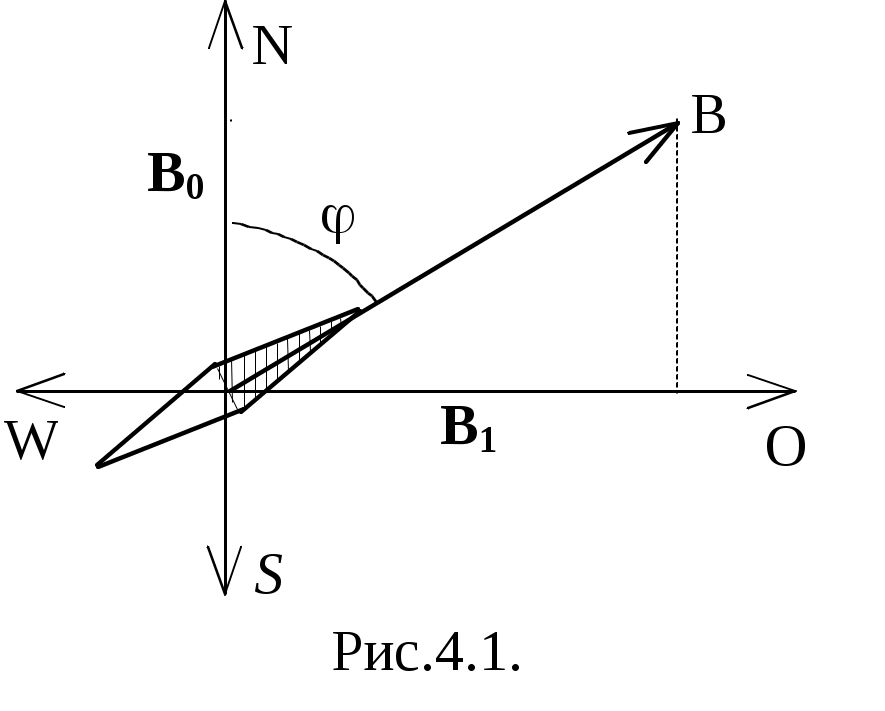 Пусть имеются два магнитных поля с индукциями B0 (создано Землей) и B1 (создано кольцевым током или полосовым магнитом), причем векторы B0и B1 перпендикулярны друг другу. Вектор B0 направлен по магнитному меридиану (в Казани практически точно на север), а вектор B1 – на восток (см. рис. 4.1).На рис 4.1. обозначены направления N – на север, S – на юг, O – на восток, W – на запад. По принципу суперпозиции B= B0 + B1. В соответствии с вышеизложенным, северный полюс магнитной стрелки компаса (на рис. 4.1 заштрихован) направлен по направлению равнодействующего вектора B. Отсюда следует Колебания полосового магнита в магнитном поле ЗемлиПодвесим полосовой постоянный магнит на очень тонкой нити в некотором магнитном поле. Поле создается каким-либо устройством или Землей.(в лабораторной работе используем магнитное поле Земли с индукцией B0). Направление вектора индукции магнитного поля B0 определяем по компасу. Численное значение его модуля нам может быть неизвестным. Ориентируем полосовой магнит по направлению вектора индукции магнитного поля B0 (в условиях эксперимента ориентируем его северным концом к N). Дождемся, пока магнит перестанет колебаться. Затем осторожно отклоним его на малый угол , не более нескольких градусов. На магнит станет действовать возвращающий момент M .В соответствии с уравнением (2.3) M = – B0 pm sin , (6.1) где pm – магнитный момент полосового магнита. При малых углах можно принять sin =. Поэтому из (6.1) получим: M = – B0 pm . (6.2) Запишем основное уравнение динамики вращательного движения M = I , (6.3) где – угловое ускорение магнита, равное I – момент инерции магнита относительно центра масс. I определяется формулой где m – масса магнита (определяется взвешиванием), с – длина магнита, b – ширина магнита (определяются измерениями). Из уравнений (6.2) и (6.3) получим I = –B0 · pm Обозначим Тогда Получено линейное однородное дифференциальное уравнение второго порядка. Общее решение уравнения имеет вид = A cos(t+ ) . Следовательно, движение магнита представляет собой гармоническое колебание с периодом С учетом (6.5) получим Из этого уравнения найдем магнитный момент pm Момент инерции I определяется по уравнению (6.4), период колебаний магнита можно получить экспериментально. Численное значение индукции B0 нам неизвестно. Для определения магнитного момента pm воспользуемся уравнением (4.6) . По уравнению (5.1) B1=B0 tg . Подставив это выражение в уравнение (4.6), получим где x – расстояние от центра полосового магнита до оси стрелки компаса.Из этого уравнения следует Подставив уравнение (6.9) в уравнение (6.7), получим искомый магнитный момент pm: Из уравнения (6.10) следует, что для определения магнитного момента pm полосового постоянного магнита необходимо вычислить по уравнению (6.4) момент инерции I магнита, период Т колебаний магнита в магнитном поле Земли, угол отклонения стрелки компаса от магнитного меридиана. Методика проведения эксперимента и обработки результатовНачертить в тетради таблицы 1 и 2. Включить компьютер. Таблица 1
Таблица2
Запустить программу 36К.ЕХЕ. Для этого указать курсором на 36К.ЕХЕ и щелкнуть левой кнопкой мышки (в дальнейшем эту команду обозначим L’ на 36К.ЕХЕ). Ввести свое имя. ОК. Установить магнитный момент полосового магнита путем перемещения ползунка вправо с помощью мышки. ОК. Изучить информацию на экране. Слева вверху показан подвешанный полосовой магнит, внизу расположена таблица 1. В правой части экрана имеется панель инструментов. Измерение периода крутильных колебаний полосового магнита.Отклонить стрелку путем перемещения ползунка вправо с помощью мышки. ОК. L’ на Магнит. Магнит начинает совершать крутильные колебания вокруг вертикальной оси, проходящей через центр масс. L’ на В таблицу в моменты завершения 10, 20 и 30 полных колебаний. Рассчитать период колебаний магнита по формуле 7. Вычислить среднее значение периода Тср и отклонение Т каждого измерения от периода Тср по формулам 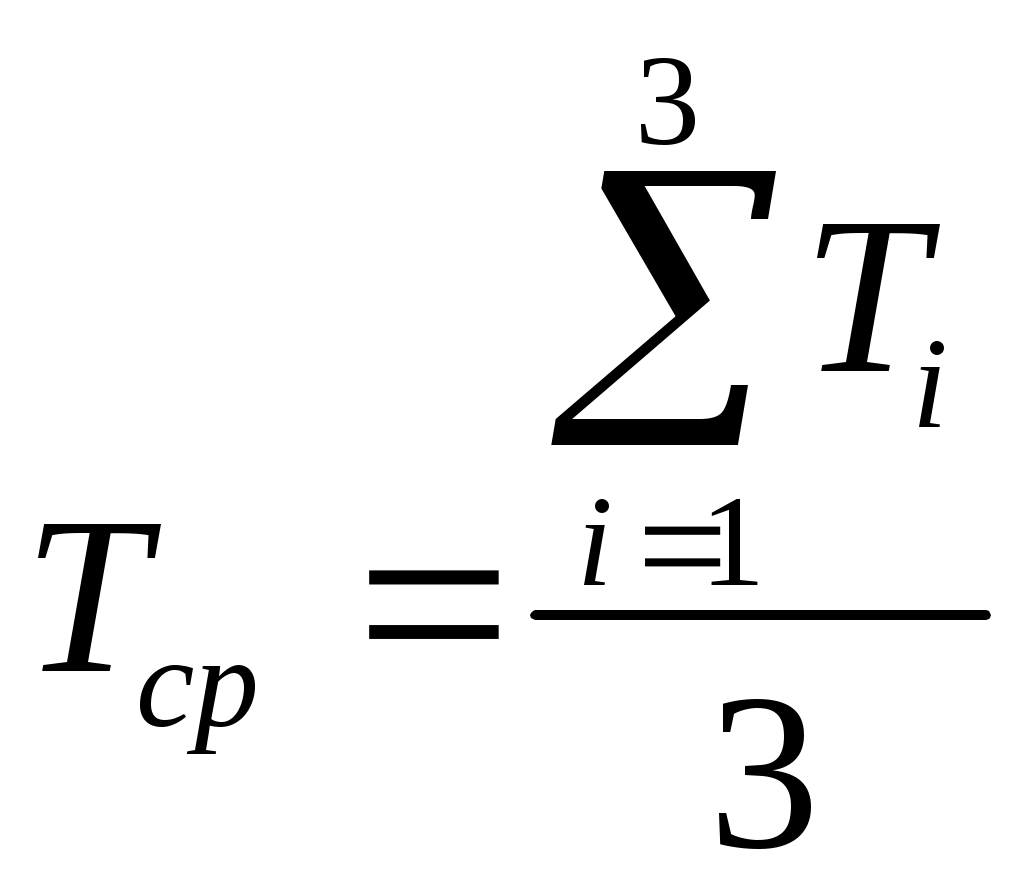 , Тi =|Tср – Тi|. , Тi =|Tср – Тi|.Результаты расчетов записать в табл. 1. 8. Вычислить: Результаты расчетов записать в табл. 1. 9. При Tср >10% повторить измерения периода Т. При Tср 10% записать полученное численное значение среднего периода Тсрв раздел «Выводы» отчета. Измерение угла отклонения стрелки компаса. 10. L’ на Перейти ко 2-ой части. На экране появляются стрелка компаса, полосовой магнит и отчет 2. Переместить мышкой полосовой магнит влево. Рядом с линейкой появляется значение x в метрах, ниже магнита – значение угла отклонения при отклонении стрелки на восток. Значения x и записать в табл. 2. Не меняя расстояния x повернуть полосовой магнит северным полюсом на восток. Для этого L’ на Направление магнита. Значения x и записать в табл. 2. L’ на Направление магнита. Значения x и записать в табл. 2. Пункт 13 повторить еще 3 раза. Вычислить среднее значение угла по формуле и записать результат расчета во все 6 строк таб. 2. Вычислить отклонения i каждого замера угла от среднего значения угла i = |i – ср| и записать результаты расчета в табл. 2. 17. Вычислить Результаты расчетов записать в табл.2. Численные значения x и ср записать в табл. 2 и в разделе «Выводы» отчета.. Показать результаты эксперимента преподавателю и получить от него разрешение (отметку в отчете) на расчет магнитного момента по формуле (6.10) и окончательному оформлению отчета. В расчетах плотность железа принять равной 7880 кг м-3. 2 2 2Контрольные вопросы Силовые линии магнитного поля. Магнитное поле Земли. Горизонтальная и вертикальная составляющие вектора индукции магнитного поля Земли. Что показывает стрелка компаса при отсутствии магнита? Каким образом с помощью компаса и полосового магнита можно определить величину индукции магнитного поля Земли? Понятие малых колебаний. Почему постоянный магнит будет совершать крутильные колебания в магнитном поле Земли? Понятие магнитного момента. Чем обусловлено наличие магнитного момента у постоянного магнита? Как Вы находили магнитный момент полосового магнита? Зачем нужно измерять угол ? |
