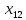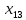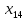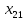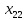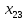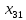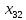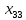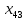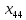шпоргалка. Лабораторная работа 4 Исследование и определение оптимального распределения поставок и минимальных затрат при решении транспортных задач
 Скачать 44.42 Kb. Скачать 44.42 Kb.
|
|
Министерство образования Республики Беларусь Белорусский национальный технический университет Кафедра “Тепловые электрические станции” Группа 10604119 Исследование и определение оптимального распределения поставок и минимальных затрат при решении транспортных Отчёт по лабораторной работе №4 по дисциплине “Методы математического программирования” Исполнитель: Пиртань А.А. Руководитель: Бадак Б.А Минск-2022 Лабораторная работа № 4 Исследование и определение оптимального распределения поставок и минимальных затрат при решении транспортных задач Цель работы: Приобретение студентами практических навыков решения транспортных задач и использования инструмента Поиск решения среды Excel для нахождения оптимального распределения поставок и минимальных затрат. Вариант 2 Транспортная компания занимается перевозкой зерна специальными зерновозами от трех элеваторов к четырем мельницам. Максимально возможное количество отгружаемых зерновозов в сутки 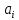 составляет 100, 120, 150, 130. Суточные потребности мельниц составляет 100, 120, 150, 130. Суточные потребности мельниц 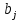 составляют 100, 130, 90 и 140 зерновозов. Затраты на перевозку зерна от i -го элеватора к j -ой мельнице в тыс. руб. представлены в виде матрицы. составляют 100, 130, 90 и 140 зерновозов. Затраты на перевозку зерна от i -го элеватора к j -ой мельнице в тыс. руб. представлены в виде матрицы.Требуется определить структуру перевозок между элеваторами и мельницами с минимальной стоимостью. 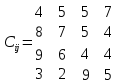 Решение: Представим исходные данные задачи в виде таблицы. Таблица 1 – Транспортная таблица
Решение транспортной задачи состоит из двух этапов. 1. Определение начального базисного допустимого решения. 2. Поиск оптимального решения транспортной задачи. Этап 1. Определение начального базисного допустимого решения. Используем метод северо-западного угла. Выполнение начинается с верхней левой ячейки (северо-западного угла) транспортной таблицы, т.е. с переменной 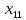 . .Шаг 1. Переменной 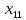 присваивается максимальное значение, допускаемое ограничениями на спрос и предложение. присваивается максимальное значение, допускаемое ограничениями на спрос и предложение.Шаг 2. Вычеркивается строка (или столбец) с полностью реализованным предложением (с удовлетворенным спросом). Это означает, что в вычеркнутой строке (столбце) мы не будем присваивать значения остальным переменным (кроме переменной, определенной на первом этапе). Если одновременно удовлетворяются спрос и предложение, вычеркивается только строка или только столбец. Шаг 3. Если не вычеркнута только одна строка или только один столбец, процесс останавливается. В противном случае переходим к ячейке справа, если вычеркнут столбец, или к нижележащей ячейке, если вычеркнута строка. Затем возвращаемся к первому этапу. Применив описанную процедуру, получим начальное базисное решение, представленное в табл. 2. В этой таблице стрелками показана последовательность определения базисных переменных. Таблица 2 – Базисное решение транспортной задачи
Получено следующее начальное базисное решение: 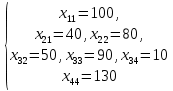 Соответствующая суммарная стоимость перевозок равна: Z =4 ⋅ 100 + 8 ⋅40 + 7 ⋅ 80 + 6 ⋅50 + 4 ⋅ 90 +4 ⋅10+5 ⋅130 = 2380 руб. Этап 2. Поиск оптимального решения транспортной задачи. Используя полученное начальное базисное решение, произведем улучшение плана перевозок. В таблице 3.2 назначим потенциалы строк и столбцов. В методе потенциалов каждой i -ой строке и каждому j -му столбцу транспортной таблицы ставятся в соответствие числа (потенциалы) 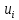 и и 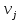 , которые для базисных переменных удовлетворяют уравнению , которые для базисных переменных удовлетворяют уравнению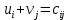 . .Примем 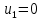 , тогда , тогда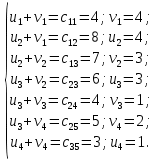 Используя найденные значения потенциалов, для каждой небазисной переменной вычислим величины оценки 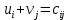 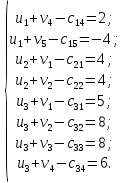 Найденные значения поместим в таблицу 3. Таблица 3 – Модифицированная транспортная таблица
Среди небазисных переменных выберем переменную, имеющую максимальное значение оценки 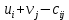 . В данном случае будет выбрана ячейка соответствующая . В данном случае будет выбрана ячейка соответствующая 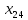 . Нам необходимо найти величину перевозок по данному маршруту θ, которая уменьшит общую стоимость перевозок. . Нам необходимо найти величину перевозок по данному маршруту θ, которая уменьшит общую стоимость перевозок.Построим замкнутый цикл перерасчета, включающий базовое распределение поставок и выбранную нами ячейку (табл. 4). Таблица 4 – Замкнутый цикл перерасчета для переменной 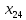 . .
Для удовлетворения ограничения по спросу и предложению, нужно поочередно отнимать и прибавлять 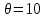 к значениям базисных переменных, выбрав из грузов к значениям базисных переменных, выбрав из грузов 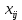 стоящих в минусовых клетках наименьшее, т.е. стоящих в минусовых клетках наименьшее, т.е. 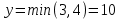 , в результате получим новое базисное решение (табл. 5): , в результате получим новое базисное решение (табл. 5):Таблица 5 – Транспортная таблица для второго базисного решения
Произведем вычисление новых значений потенциалов для строк и столбцов, по описанной выше методике. Определим для каждой небазисной переменной величины оценки 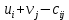 . Результаты приведены в табл. 6 . Результаты приведены в табл. 6Таблица 6 – Модифицированная транспортная таблица (2)
Выбираем максимальное значение величины оценки, соответствующее ячейке 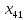 . Строим замкнутый цикл (табл. 7). . Строим замкнутый цикл (табл. 7).Таблица 7 – Замкнутый цикл перерасчета для переменной 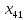
Новое решение показано в табл. 8. Таблица 8 – Транспортная таблица для третьего базисного решения
Произведем вычисление новых значений потенциалов для строк и столбцов, по описанной выше методике. Определим для каждой небазисной переменной величины оценки 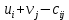 . Результаты приведены в табл. 9 . Результаты приведены в табл. 9Таблица 9 – Модифицированная транспортная таблица (3)
Выбираем максимальное значение величины оценки, соответствующее ячейке 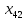 . Строим замкнутый цикл (табл. 10). . Строим замкнутый цикл (табл. 10).Таблица 10 – Замкнутый цикл перерасчета для переменной 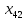
Новое решение показано в табл. 8. Таблица 8 – Транспортная таблица для третьего базисного решения
Таблица 9 – Модифицированная транспортная таблица (3)
Таблица 10 – Замкнутый цикл перерасчета для переменной 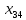
Новое решение показано в табл. 11. Таблица 11 – Транспортная таблица для четвертого базисного решения
Находим значение 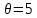 и исключаем переменную . и исключаем переменную .
Все значения величин оценки небазисных переменных отрицательные. Это указывает на то, что найденное решение транспортной задачи оптимально. Минимальные затраты составят: Z =4 ⋅ 100 + 4 ⋅120 + 6 ⋅ 40 + 4 ⋅90 + 5 ⋅ 20 +3 ⋅40+2 ⋅90 = 1880 руб. Использование среды Excel для решения транспортных задач Программа Excel, используемая для нахождения оптимального распределения поставок и минимальных затрат в транспортных задачах приведена на рис.1 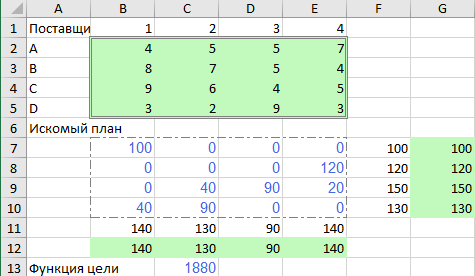 Рисунок 1 лаб4.xlsx | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||