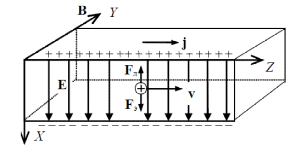
№4 Исследование магнитных полей различной конфигурации. Лабораторная работа 4 исследование магнитных полей различной конфигурации

• Название: Лабораторная работа 4 исследование магнитных полей различной конфигурации
• Дата: 02.11.2022
• Размер: 1.77 Mb.
• Имя файла: №4 Исследование магнитных полей различной конфигурации.doc
• Тип: Лабораторная работа; #767943

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение

высшего образования

Санкт-Петербургский горный университет


Кафедра общей и технической физики


общая физика

Лабораторная работа № 4
ИССЛЕДОВАНИЕ

МАГНИТНЫХ ПОЛЕЙ

РАЗЛИЧНОЙ КОНФИГУРАЦИИ
Методические указания к лабораторной работе

САНКТ-ПЕТЕРБУРГ 2021
Цель работы: Измерение магнитной индукции полей, создаваемых проводниками с током различной конфигурации. Экспериментальная проверка закона Био–Савара–Лапласа.

1. Теоретические основы лабораторной работы

Существуют различные противоречивые сведения о первом упоминании магнитов в истории человечества. Согласно одним оценкам, магнетит или магнитный железняк впервые был открыт в Китае за четыре тысячи лет до н. э. В то же время западные исследователи отдают приоритет в открытии магнетизма древним грекам.

Первые упоминания в летописях о применении магнитных материалов восходят к третьему тысячелетию до н. э., когда китайский император Хуан-ди использовал компас во время сражения. В целом, время изобретения компаса оценивается между 2637 и 1100 гг до н. э.

Возможно, слово «магнит» происходит от др.-греч. Μαγνῆτις λίθος (Magnētis líthos), «камень из Магнесии». Регион Магнисия и древний город Магнесия располагались в Малой Азии, где в древности были открыты залежи природного магнетита. Считается, что целенаправленное исследование магнитного поля началось в 1269 г, когда французский ученый Петр Перегрин (рыцарь Пьер из Мерикура) изучал магнитное поле сферического магнита, применяя стальные иглы. Перегрин определил, что наибольшее «скопление» игл происходило в двух точках постоянного магнита, которые он назвал «полюсами» по аналогии с полюсами Земли.

В 1600 г вышло сочинение придворного врача королевы Елизаветы I У. Гилберта «О магните», в котором впервые была предпринята попытка создать теорию магнетизма. К уже известным фактам Гилберт добавил собственные наблюдения: усиление действия магнитных полюсов железными брусками и потерю намагничивания при нагревании. Гилберт одним из первых высказал гипотезу, что Земля обладает собственным магнитным полем.

В 1750 г Дж. Мичелл предположил, что магнитные полюса притягиваются и отталкиваются с силой, которая обратно пропорциональна квадрату расстояния. В 1785 г Ш. Кулон экспериментально доказал это утверждение и сформулировал предположение о том, что Северный и Южный полюсы одного магнита не могут быть разделены.

В 1820 г датский физик Г. Эрстед, пытаясь на лекции продемонстрировать студентам, отсутствие связи между электричеством и магнетизмом, включил электрический ток вблизи магнитной стрелки компаса. Он был удивлен, увидев, что магнитная стрелка после включения тока начала совершать колебания. Эрстед сумел оценить значение своего наблюдения и многократно повторил опыт, протянув провод горизонтально и параллельно свободно подвешенной магнитной стрелке. При включении тока, стрелка немедленно отклонялась, стремясь занять положение перпендикулярное к направлению провода. При изменении направления тока стрелка отклонялась в другую сторону.

Узнав об открытии Эрстеда, французский физик Д. Араго провел собственную серию опытов, в которой он намагничивал металлические предметы с помощью магнитного поля электрического тока. Тем самым, Араго доказал, что проводник, по которому идет ток, представляет собой магнит.

Объяснение описанных явлений было дано французским физиком А. Ампером, который установил внутреннюю связь между электричеством и магнетизмом. В сентябре 1820 г на заседании Французской Академии наук он сообщил о полученных результатах. В своих опытах Ампер впервые использовал спирально скрученный проводник, который при пропускании электрического тока приобретал свойства магнита. Такой проводник Ампер назвал соленоидом (от греч. solen ‑ канал, труба и eidos ‑ подобный). В том же 1820 гАмпер показал, что параллельные провода, по которым идет ток в одном и том же направлении, притягиваются друг к другу.

Для объяснения своих опытов Ампер в 1825 г предположил, что магнетизм можно объяснить «молекулярными» круговыми токами. Он считал, что магнит состоит из молекул, в которых имеются собственные круговые токи. Такие «молекулярные» токи превращают каждую молекулу в микроскопический магнитик. Если по какой-либо причине такие магнитики выстроятся одноименными полюсами в одну и ту же сторону, то они образуют большой магнит. Эта гипотеза объясняла, почему магнитный заряд не может быть изолирован.

В 1831 г М. Фарадей открыл электромагнитную индукцию (ЭМИ), при которой переменное магнитное поле порождает переменный электрический ток. Позже Ф. Нейман дал математическую формулировку закона ЭМИ. При этом он определил векторный потенциал электромагнитного поля. Именно М. Фарадей в 1845 г впервые ввел термин «магнитное поле».

Между 1861 и 1865 гг Дж. Максвелл разработал и опубликовал систему уравнений, которая объяснила и объединила все известные электрические и магнитные явления в классической физике. Законченная теория Максвелла была опубликована в работе 1865 г «Динамическая теория электромагнитного поля», в которой Максвелл предположил, что свет представляет собой электромагнитные волны. В 1887 г Г. Герц экспериментально подтвердил этот факт.

В 1892 г Х. Лоренц вывел силу Ампера для взаимодействия двух проводников из уравнений Максвелла. При этом создание классической теории электродинамики было в основном закончено.
Закон Био – Савара – Лапласа
Данный физический закон был экспериментально установлен в 1820 г Б. Био (1774-1862) и Ф. Саваром (1791-1841) и сформулирован в общем виде П-С. Лапласом (1749-1827). Лаплас также показал, что с помощью этого закона можно вычислить магнитное поле движущегося точечного заряда (считая, что движущейся заряженной частице можно сопоставить элементарный ток).

Закон Био – Савара – Лапласа играет в магнитостатике ту же роль, что и закон Кулона в электростатике, поскольку позволяет вместе с принципом суперпозиции определять вектор индукции магнитного поля, создаваемого постоянным током сложной конфигурации. В современной физике закон Био – Савара – Лапласа является следствием уравнений Максвелла, однако исторически его открытие предшествовало уравнениям Максвелла, поэтому закон Био – Савара – Лапласа в курсе физики изучается вне связи с уравнениями Максвелла. При этом следует помнить, что уравнения Максвелла выступают как более фундаментальные, поскольку закон Био – Савара – Лапласа нельзя применять в случае переменных токов.

Как известно, движущиеся заряды и проводники с токами создают в пространстве магнитное поле. Это поле проявляется в том, что на движущиеся в нем заряды действуют силы. Силовую характеристику магнитного поля называют магнитной индукциейи обозначают как . Единица измерений магнитной индукции в СИ – тесла [Тл].

Из опыта известно, что магнитное поле имеет направленный характер, поэтому индукция магнитного поля – векторная величина. Для магнитного поля справедлив принцип суперпозиции: магнитное поле, создаваемое несколькими движущимися зарядами или токами, равно векторной сумме магнитных полей, создаваемых каждым зарядом или током в отдельности, т.е.
. (1)

Б. Био и Ф. Савар экспериментально установили, что магнитная индукция для любых форм проводников пропорциональна силе тока, создающей магнитное поле, и зависит от расстояния до той точки, в которой определялась величина вектора .

П.-С. Лаплас проанализировал экспериментальные данные, полученные Био и Саваром, и нашел, что магнитное поле любого тока может быть вычислено как векторная сумма (суперпозиция) полей, создаваемых отдельными элементарными участками тока . Маг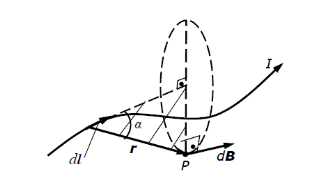нитная индукция поля, создаваемого элементом тонкого проводника с током I и длиной dl (рис. 1), определяется выражением:

, (2)

где  Гн/м – магнитная постоянная;  – вектор, совпадающий с элементарным участком тока и направленный по току I;   – радиус-вектор, проведенный от элемента тока в точку P, в которой определяется поле.


Рис. 1. Магнитная индукция от элемента проводника с током

Проинтегрировав формулу (2) по всем элементам провода, получим выражение для результирующего поля всего проводника:
. (3)
Формула (3) является одним из аналитических выражений закона Био – Савара – Лапласа. Выражение (3) можно представить в скалярной форме
, (4)
где ‑ угол между и .

Для наглядного изображения магнитного поля используют линии магнитной индукции, которые проводятся так, чтобы касательная к ним в каждой точке совпадала с направлением вектора , а густота линий соответствовала модулю этого вектора в данной точке пространства (рис. 2).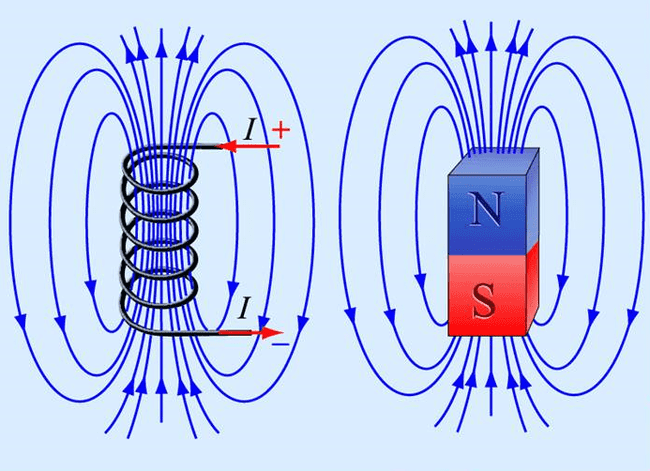

Рис. 2. Силовые линии магнитного поля соленоида и полосового магнита
Исходя из закона Био – Савара – Лапласа можно доказать, что циркуляция вектора по произвольному замкнутому контуруL равна произведению магнитной постоянной 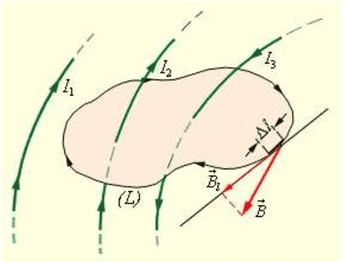на алгебраическую сумму токов, охватываемых этим контуром:
. (5)

Рис. 3. Иллюстрация теоремы о циркуляции

Выражение (5) справедливо только для поля в вакууме. Вычисляя сумму токов в правой части уравнения (5), положительным нужно считать ток, направление которого связано с направлением обхода по контуру L с правилом правого винта (рис. 3). Так, например, на рисунке 3: ; . Выражение (5) называют теоремой о циркуляции вектора. Тот факт, что циркуляция вектора не равна нулю, означает, что магнитное поле не потенциально. Такое поленазывают вихревым.

Теорема о циркуляциипозволяет доказать, что внутри длинного соленоида, с отношением длины соленоида к его диаметру не меньше 10, магнитное поле однородно и его индукция равна
, (6)
где n – число витков соленоида, приходящееся на единицу его длины; I – сила тока в соленоиде.
Примеры нахождения магнитных полей с помощью

теоремы Био – Савара – Лапласа
1. Магнитное поле прямолинейного проводника с током
Рассмотрим магнитное поле, создаваемое прямолинейным проводником с током конечной длины (рис. 4). Отдельные элементарные участки такого проводника создают поля , направленные в одну сторону (перпендикулярно плоскости чертежа), поэтому индукция магнитного поля в точке М может быть найдена интегрированием:

. (7)

Согласно рис. 4, имеем 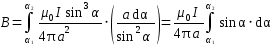и . Тогда, после подстановки в (7) получим
.
После интегрирования с учетом того, что для конечного проводника угол меняется от ₁ до ₂, для искомой магнитной индукции в точке М получим

, (8)
где a – кратчайшее расстояние от точки M до проводника с током, ₁ и ₂ – углы между концами проводника и соответствующими радиус-векторами.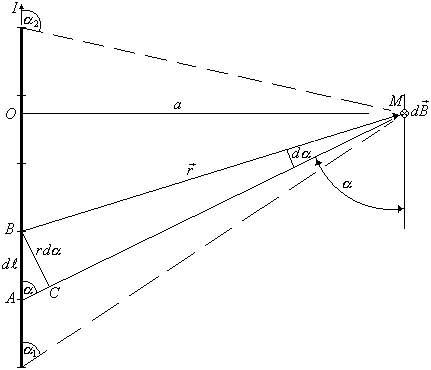

Рис. 4. Магнитное поле прямолинейного отрезка с током
Если определять магнитную индукцию в точках, расположенных на перпендикуляре, восстановленном к середине проводника длиной 2l, то , следовательно,

. (9)
С учетом выражения (9) формулу (8) можно записать в виде

. (10)

В том случае, когда длина проводника (проводник бесконечной длины), формулу (10) можно записать в виде:

. (11)
2. Магнитное поле на оси короткой катушки с током
Рассмотрим магнитное поле тока, протекающего по тонкому проводу в виде окружности радиусом R (круговой ток). Найдем магнитную индукцию на оси кругового тока на расстоянии 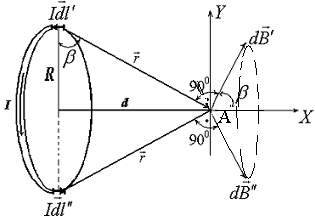от центра контура (рис. 5). Элемент тока создает в точке А согласно закона Био – Савара – Лапласа индукцию, модуль которой равен
. (12)


Рис. 5. Магнитное поле на оси кругового витка

От всех элементов тока будет образовываться конус векторов . Легко заметить, что любому элементу контура найдется элемент на противоположной стороне кольца, который будет создавать проекцию магнитного поля на ось OY такую же как от но противоположного направления. Таким образом, из соображений осевой симметрии можно заключить, что результирующий вектор в точке А будет направлен только вдоль оси ОX. Это значит, что для нахождения модуля этого вектора необходимо сложить проекции векторов на ось OX:
. (13)
Интегрируя выражение (13) по всему контуру с током и учитывая, что 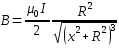, получим

. (14)
Формула (14) определяет величину магнитной индукции на оси кругового тока в координате х.

Используя формулу (14) можно найти магнитное поле в центре кольца. Для этого в (14) нужно взять х = 0:
. (15)
Рассмотрим кольцо с током, которое представляет собой короткую катушку, состоящую из N витков одинакового радиуса. Из-за осевой симметрии и в соответствии с принципом суперпозиции магнитное поле такой катушки на оси OХ представляет собой алгебраическую сумму полей отдельных витков : . Таким образом, магнитное поле короткой катушки, содержащей N витков, в произвольной точке оси Х рассчитывается по формуле

. (16)
3. Магнитное поле соленоида с током
Для расчета индукции магнитного поля в соленоиде воспользуемся теоремой о циркуляции вектора магнитной индукции:

, (17)

где – алгебраическая сумма токов, охватываемых контуром L произвольной формы; N – число проводников с токами, охватываемых контуром. При этом каждый ток учитывается столько раз, сколько раз он охватывается контуром, а положительным считается ток, направление которого образует с направлением обхода по контуру правовинтовую систему, – элемент контура L.

Применим теорему о циркуляции к соленоиду, длиной l, имеющим N_с витков с силой тока I (рис. 6).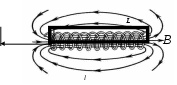



Рис. 6. Соленоид с током и силовые линии магнитного поля
Будем считать, что практически все поле сосредоточено внутри соленоида и является однородным (краевыми эффектами пренебрегаем). Тогда формула (17) примет вид:
,

откуда находим индукцию магнитного поля, создаваемую током внутри соленоида:

. (18)

Формула (18) определяет магнитное поле внутри пустого соленоида. Если внутрь соленоида поместить ферромагнитный сердечник с магнитной проницаемостью , формула (18) преобразуется к виду.

.
В рассматриваемой лабораторной работе используется соленоид без сердечника, следовательно .

4. Магнитное поле короткой катушки с током
Рассмотрим соленоид конечной длины l(короткая катушка). На рис. 7 изображен полученный экспериментально график зависимости магнитной индукции на оси некоторой катушки как функция продольной координаты z. Нетрудно заметить, что магнитное поле остается однородным только в центре катушки и изменяется до нулевого значения к краям катушки.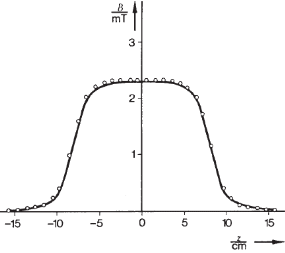

2. Рис. 7. Зависимость магнитного поля от продольной координаты

3. внутри короткой катушки

4. Для нахождения магнитного поля внутри короткой катушки рассмотрим ее поперечное сечение (рис. 8).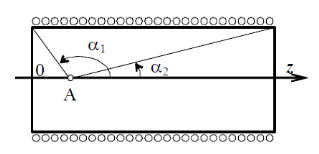

Рис. 8. Поперечное сечение короткой катушки
Можно показать, что в любой точке А, расположенной внутри катушки на ее центральной продольной оси, магнитное поле можно рассчитать с помощью формулы (14) и принципа суперпозиции. В результате получится формула:

, (19)

где N – число витков; ‑ число витков на единицу длины; I – сила тока в катушке; и ‑ углы, под которыми видны конца катушки из точки А.

5. Поскольку в лабораторной работе магнитное поле измеряется как функция продольной координаты z, формулу (19) удобнее записать в другом виде:

, (20)

6. где и ; R – радиус поперечного сечения катушки.

8. Описание экспериментальной установки

На рис. 9 и 10 изображены лабораторная установка и принципиальная электрическая схема для изучения магнитного поля проводников различной конфигурации.

Рис. 9. Внешний вид лабораторной установки



Рис. 10. Принципиальная электрическая схема установки
1 – измеритель индукции магнитного поля (тесламетр), А – амперметр, 2 – соединительный провод, 3 – измерительный щуп, 4 – датчик Холла, 5 – исследуемый объект (короткая катушка, прямой проводник, соленоид), 6 – источник тока, 7 – линейка для фиксирования положения датчика, 8 – держатель щупа
Для измерения индукции магнитного поля в лабораторной работе используется тесламетр, работающий на основе эффекта Холла. В основе эффекта Холла лежит явление возникновения поперечного электрического поля в проводнике с током, когда к проводнику приложено поперечное магнитное поле.

Рассмотрим прямоугольный проводник с положительными носителями заряда величины q, по которому течет электрический ток плотности вдоль оси Z (рис. 11).

Рис. 11. Эффект Холла
При приложении поперечного магнитного поля с индукцией вдоль оси ОY на движущиеся заряды начинает действовать магнитная сила Лоренца , направленная перпендикулярно вектору скорости . На рис. 11 сила Лоренца направлена противоположно оси ОX. Данная сила вызывает поперечное смещение зарядов, благодаря чему на верхней поверхности появляется положительный поверхностный заряд, на нижней – отрицательный. Когда электрическое поле от этих зарядов возрастет до такой величины, что электрическая сила полностью скомпенсирует силу Лоренца, накопление зарядов прекратится, и в толще проводника все заряды дальше будут двигаться строго вдоль оси Z. Приравнивая эти силы по модулю, получим . Это электрическое поле вызывает появление разности потенциалов между верхней и нижней поверхностью проводника , которая прямо пропорциональна индукции поля B. Это напряжение называется ЭДС Холла и ее можно измерить вольтметром, шкалу которого можно проградуировать в единицах магнитной индукции.

Обычно датчики Холла изготавливаются из полупроводников, в которых, в отличие от металлов, движение зарядов хорошо описывается приведенной выше классической теорией, и экспериментальная ЭДС Холла с хорошей точностью прямо пропорциональна величине поля. Преимуществами датчиков Холла являются их малые размеры (менее 1 мм²) и очень малая инерционность, что позволяет использовать их на частотах вплоть до 10¹⁰ Гц.

9. Порядок выполнения лабораторной работы

1. Исследование магнитного поля витка с током
1.1.  Включить приборы. Выключатели источника питания и тесламетра расположены на задних панелях приборов с левой стороны.

1.2.  В качестве исследуемого объекта (5) (см. рис. 10) установить в держатель виток с током и подключить его к источнику тока (6).

1.3.  Регулятор напряжения на источнике (6) поставить в среднее положение. Установить силу тока, равную нулю, путем регулировки выхода силы тока на источнике (6) и произвести контроль по амперметру (значение должно быть равно нулю).

1.4.  Регуляторами грубой 1 и тонкой настройки 2 (рис. 12) добиться нулевых показаний тесламетра.






1 2

Рис. 12. Внешний вид тесламетра
1.5.  Установить держатель с измерительным щупом на линейке в некотором удобном для считывания положении – например, в координате 300 мм. В дальнейшем принять это положение за нулевое. Следить при установке и в процессе измерений за параллельностью между щупом и линейкой.

1.6.  Расположить держатель с витком таким образом, чтобы датчик Холла (4) находился в центре витка (рис. 13). Для этого использовать регулировочный винт по высоте на держателе измерительного щупа. Плоскость витка должна быть перпендикулярна щупу. В процессе подготовки измерений перемещать держатель с исследуемым образцом, оставляя неподвижным измерительный щуп.



Рис. 13. Внешний вид витка

1.7.  Убедиться, что за время прогрева тесламетра, его показания остались нулевыми. Если это условие не выполнено, следует повторить п.п. 1.4.

1.8.  Установить максимальную силу тока в витке 4 А (путем регулировки выхода на источнике питания (6)).

1.9.  Измерить магнитную индукцию B_эксп на оси витка в зависимости от расстояния до его центра. Для этого смещать держатель измерительного щупа по линейке, сохраняя параллельность своему первоначальному положению. Отрицательные значения z соответствуют смещению щупа в область меньших координат, чем начальная, и наоборот – положительные значения z – в области больших координат. Полученные данные занести в таблицу 1.
Таблица 1

z	см	-8	-7	…	-1	0	1	…	7	8
Bэксп	мТл
Bтеор	мТл

1.10.  Измерить зависимость индукции в центре витка при z = 0 от силы тока, протекающего по нему. Сила тока не должна превышать 4 А. Данные занести в таблицу 2.
Таблица 2

I	A	0	0,5	1,0	1,5	2,0	2,5	3,0	3,5	4,0
Bэксп	мТл
Bтеор	мТл

2. Исследование магнитного поля короткой катушки с током
2.1.  В качестве исследуемого объекта 5 установить короткую катушку на регулируемую по высоте металлическую скамью из немагнитного материала (рис. 14).


Рис. 14. Внешний вид короткой катушки
2.2.  Повторить п.п. 1.3 – 1.5.

2.3.  Отрегулировать высоту скамьи так, чтобы измерительный щуп проходил по оси катушки, а датчик Холла оказался в середине витков короткой катушки.

2.4.  Повторить пункты 1.7 – 1.10 (вместо витка используется короткая катушка). Данные занести соответственно в таблицы 3 и 4. При этом координату центра катушки определить следующим образом: установить датчик Холла в начало катушки и зафиксировать координату держателя. Затем передвигать держатель по линейке вдоль оси катушки до тех пор пока конец датчика не окажется на другой стороне катушки. Зафиксировать координату держателя в этом положении. Координата центра катушки будет равна среднему арифметическому из двух измеренных координат.
Таблица 3

z	см	-10	-9	…	-1	0	1	…	9	10
Bэксп	мТл
Bтеор	мТл

2.5.  Повторить пункты 1.3 – 1.7.

2.6.  Измерить зависимость индукции в центре короткой катушки от силы тока, проходящего через нее. Сила тока не должна превышать 4 А. Данные занести в таблицу 4.

Таблица 4

I	A	0	0,5	1,0	1,5	2,0	2,5	3,0	3,5	4,0
Bэксп	мТл
Bтеор	мТл
L	мкГн

3. Исследование магнитного поля соленоида с током
3.1.  В качестве исследуемого объекта 5 установить соленоид на регулируемую по высоте металлическую скамью из немагнитного материала (рис. 15).

Рис. 15. Внешний вид соленоида
3.2.  Повторить п.п. 1.3 – 1.5.

3.3.  Отрегулировать высоту скамьи так, чтобы измерительный щуп проходил по оси симметрии соленоида, а датчик Холла оказался в середине витков соленоида.

3.4.  Повторить пункты 1.7 – 1.10 (вместо короткой катушки здесь используется соленоид). Данные занести соответственно в таблицы 5 и 6. При этом координату центра соленоида определить следующим образом: установить датчик Холла в начало соленоида и зафиксировать координату держателя. Затем передвигать держатель по линейке вдоль оси соленоида до тех пор пока конец датчика не окажется на другой стороне соленоида. Зафиксировать координату держателя в этом положении. Координата центра соленоида будет равна среднему арифметическому из двух измеренных координат.
Таблица 5

z	см	-10	-9	…	-1	0	1	…	9	10
Bэксп	мТл
Bтеор	мТл

3.5.  Повторить пункты 1.3 – 1.7.

3.6.  Измерить зависимость индукции в центре соленоида от силы тока, проходящей через катушку. Сила тока не должна превышать 4 А. Данные занести в таблицу 6.

Таблица 6

I	A	0	0,5	1,0	1,5	2,0	2,5	3,0	3,5	4,0
Bэксп	мТл
Bтеор	мТл

10. Обработка результатов измерений

1.  По формуле (16) найти теоретически рассчитанную магнитную индукцию, создаваемую витком с током. При этом следует учесть, что , см. Полученные данные занести в таблицы 1 и 2. По данным таблицы 1 построить теоретическую и экспериментальную зависимости магнитной индукции на оси витка от расстояния z до центра витка. Теоретическую и экспериментальную зависимости построить в одних координатных осях.

2.  По данным таблицы 2 построить теоретическую и экспериментальную зависимости магнитной индукции в центре витка от силы тока в нем. Теоретическую и экспериментальную зависимости построить в одних координатных осях.

3.  По формуле (20) найти теоретически рассчитанную магнитную индукцию, создаваемую короткой катушкой. При этом следует учесть, что , см, см. Полученные данные занести в таблицы 3 и 4. По данным таблицы 3 построить теоретическую и экспериментальную зависимости магнитной индукции на оси короткой катушки от расстояния z до ее центра. Теоретическую и экспериментальную зависимости построить в одних координатных осях.

4.  По данным таблицы 4 построить теоретическую и экспериментальную зависимости магнитной индукции в центре короткой катушки от силы тока в ней. Теоретическую и экспериментальную зависимости построить в одних координатных осях.

5.  По формуле (18) найти теоретически рассчитанную магнитную индукцию, создаваемую в центре соленоида (краевыми эффектами пренебречь). При этом следует учесть, что , мм, см. Данные занести в таблицы 5 и 6. По данным таблицы 5 построить теоретическую и экспериментальную зависимости магнитной индукции на оси соленоида от расстояния z до его центра. Теоретическую и экспериментальную зависимости построить в одних координатных осях.

6.  По данным таблицы 6 построить теоретическую и экспериментальную зависимости магнитной индукции в центре соленоида от силы тока в нем. Теоретическую и экспериментальную зависимости построить в одних координатных осях.

7.  Рассчитать индуктивность соленоида L. Сопоставить полученное среднее значение L со справочным значением индуктивности L = 90 мкГн. Для расчета воспользоваться формулой , где  – потокосцепление,  = N_сBS, где В – магнитная индукция в соленоиде (по данным таблицы 4), S = d²/4 – площадь поперечного сечения соленоида.

8.  Рассчитать погрешности косвенных вычислений L.

11. Контрольные вопросы

1. Что такое магнитное поле, чем оно создается, вектор индукции магнитного поля и единицы ее измерения.

2. В чем заключается закон Био – Савара – Лапласа и как его можно применять при расчете магнитных полей проводников с током?

3. Как определяется направление вектора магнитной индукции в законе Био – Савара – Лапласа?

4. Как измеряется магнитное поле в данной работе? На каком физическом явлении основан принцип измерения магнитного поля?

5. Дайте определение индуктивности, магнитного потока, потокосцепления. Укажите единицы измерения этих величин.

6. Исходя из закона Био и Савара, получить величину индукции магнитного поля на оси тонкого витка с током.

7. Исходя из закона полного тока, найти магнитную индукцию вокруг бесконечного проводника с током;

8. Исходя из закона полного тока, найти магнитную индукцию внутри бесконечно длинного соленоида на его оси.

9. В чем состоит эффект Холла и как он используется для измерения магнитного поля?

10. Почему датчики Холла делают из легированных полупроводников?
библиографический список

1. 
   Калашников Н.П. Основы физики. М.: Дрофа, 2004. Т. 1
   
2. 
   Савельев И.В. Курс физики. СПб.: Лань, 2016. Т. 2.
   
3. 
   Детлаф А.А., Яворский Б.М. Курс физики. М.: ACADEMIA, 2005.
   
4. 
   Иродов И.Е. Электромагнетизм. М.: Лань, 2009.
   
5. 
   Трофимова Т.И. Курс физики. М.: Академия, 2015.
   
6. 
   Детлаф А.А., Яворский Б.М.. Справочник по физике. М.: Наука, 2008.