лаба 4. Лабораторная работа 4 Исследование магнитного поля на оси кольцевых катушек Преподаватель кафедры
 Скачать 227.47 Kb. Скачать 227.47 Kb.
|
|
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Уральский государственный университет путей сообщения» (ФГБОУ ВПО УрГУПС) Кафедра: «Физики и химии» Лабораторная работа №4 «Исследование магнитного поля на оси кольцевых катушек» Руководитель: Преподаватель кафедры «Физики и химии» Суетин Д.В. Выполнил: Студент группы СТ-127 Рахимова А.И. Екатеринбург 2018 Цель работы: Измерить магнитную индукцию в различных точках на оси кольцевой катушки, или двух катушек, смещенных относительно друг друга, при их согласном и встречном включении. Построить график её изменения вдоль оси. Проверить результаты измерения с помощью расчета, по принципу суперпозиции. Схема установки. 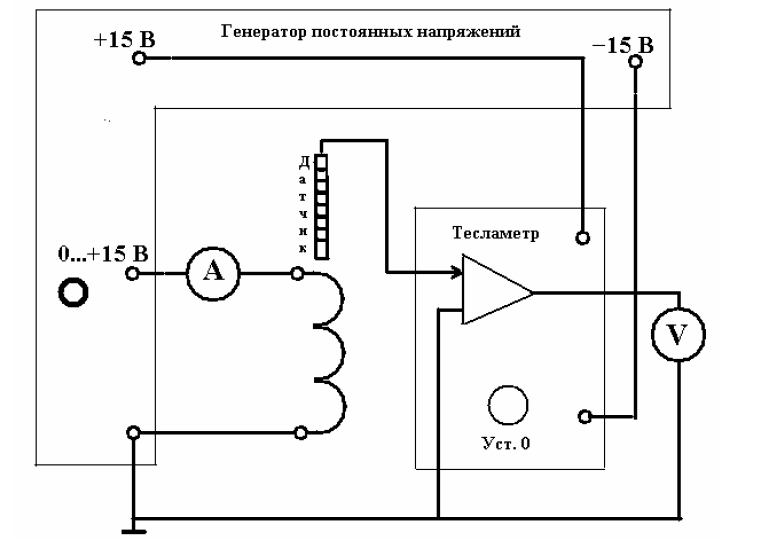 Электрическая схема установки. Теоретическая часть. Магнитное поле действует на движущиеся электрические заряды. Величина этого действия на отдельный движущийся заряд определяется силой Лоренца. Сила Ампера является суммой сил Лоренца, действующих на движущиеся заряды в проводнике с током. 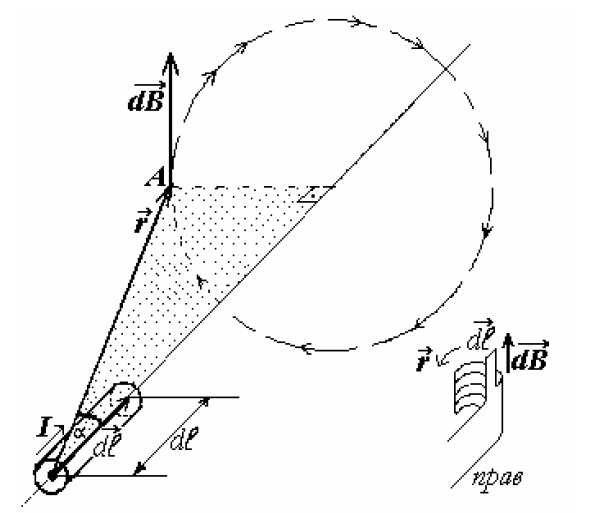 Рис.1. Создание магнитного поля током в участке проводника. Закон Био-Савара в форме, предложенной Лапласом, записывается в виде d 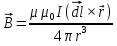 (1) (1)где 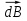 – магнитная индукция, созданная в точке А током силой – магнитная индукция, созданная в точке А током силой 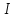 в коротком проводнике длиной dl(рис.1.); в коротком проводнике длиной dl(рис.1.);μ − магнитная проницаемость среды; μ0 = 4π⋅ 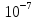 Гн/м − магнитная постоянная; Гн/м − магнитная постоянная;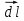 − вектор, равный по модулю длине dl бесконечно малого проводника и − вектор, равный по модулю длине dl бесконечно малого проводника инаправленный вдоль направления электрического тока (на рис.1 ток направлен за чертеж); 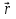 − радиус-вектор точки А с началом на проводнике; − радиус-вектор точки А с началом на проводнике;r − расстояние от проводника до точки А. Вектор 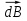 перпендикулярен плоскости, в которой лежат векторы перпендикулярен плоскости, в которой лежат векторы 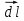 и и 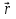 . .Закон Био-Савара (1.1) для магнитного поля участка тока I 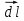 аналогичен закону Кулона для электрического поля заряда dq. аналогичен закону Кулона для электрического поля заряда dq.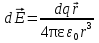 (2) (2) Для модуля (абсолютной величины) dB=|d 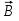 | из (1) получаем | из (1) получаем 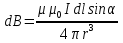 (3) (3)Здесь α − угол между векторами 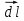 и и 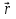 (см. рис.1). (см. рис.1).Магнитное поле на оси соленоида. Рассмотрим соленоид радиусом R и длиной L , по которому течет ток I (рис.2). Выделим на соленоиде на расстоянии 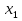 от его левого края бесконечно узкое кольцо шириной от его левого края бесконечно узкое кольцо шириной 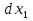 . Число витков dN в этом кольце равно числу витков в единице длины соленоида w , умноженному на ширину кольца . Число витков dN в этом кольце равно числу витков в единице длины соленоида w , умноженному на ширину кольца 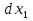 , ,dN = w 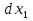 (4) (4)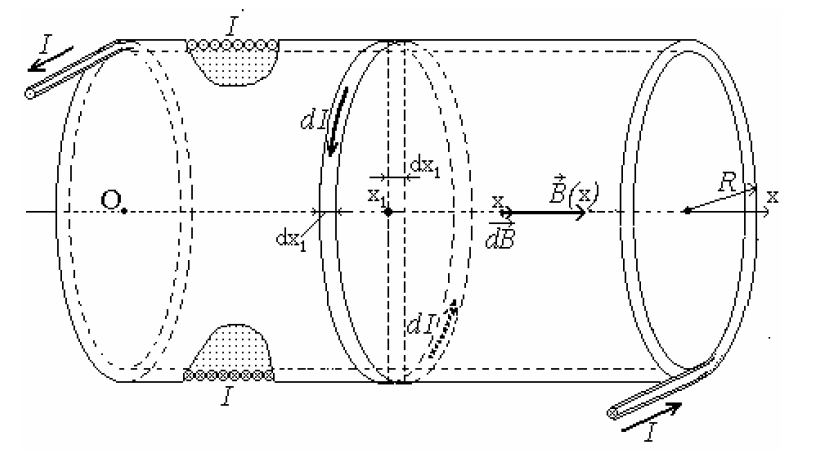 Рис.2. Магнитное поле на оси кольца с током. Число w называется плотностью числа витков соленоида. Сила тока dl в выделенном кольце равна dl = dN = Iw 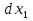 (5) (5)Направим ось Ox вдоль оси соленоида, выбрав начало координат O на левом краю соленоида. В точке A с координатой x , которая отстоит от выделенного кольца на расстоянии ( 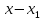 ), модуль ), модуль 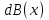 магнитной индукции магнитной индукции 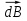 (x), (x),созданной током dI в выделенном кольце, равен: 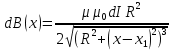 (6) (6)После подстановки (5) в (6) : 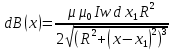 (7) (7)Модуль 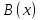 магнитной индукции магнитной индукции 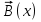 , созданной в точке A током во всем соленоиде, равен интегралу от выражения (7) при изменении координаты выделенного кольца , созданной в точке A током во всем соленоиде, равен интегралу от выражения (7) при изменении координаты выделенного кольца 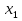 от 0 до L: от 0 до L: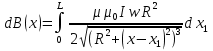 (8) (8) 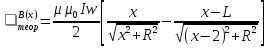 (9) (9)Напряженность магнитного поля  связана с магнитной индукцией связана с магнитной индукцией 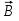 формулой: формулой: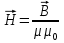 (10) (10)Выражение для модуля напряженности магнитного поля H(x) в точке A на оси соленоида: 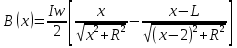 (11) (11)В середине длинного соленоида, длина L которого много больше его радиуса R, из (11) имеем ( 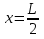 и L >> R ). и L >> R ).Н( 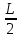 ) = ) = 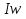 (12) (12)Экспериментальное значение магнитной индукции: 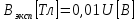 (13) (13)Для смещенной катушки ( с координатой х=0) индукция поля 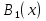 в зависимости от расстояния х по формуле тонкой кольцевой катушки с числом витков N. в зависимости от расстояния х по формуле тонкой кольцевой катушки с числом витков N.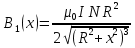 (14) (14) Для смещенной катушки ( с координатой х=a) индукция поля 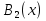 в зависимости от расстояния х по формуле: в зависимости от расстояния х по формуле: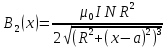 (15) (15) При последовательном согласном включении катушек ток в них течет в одном направлении, поэтому, согласно принципу суперпозиции полей, магнитная индукция: 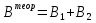 (16) (16) Геометрические размеры, входящие в формулу, изображены на рис.4. При расчёте принять R=0,007м, N=250, a=0,005м. 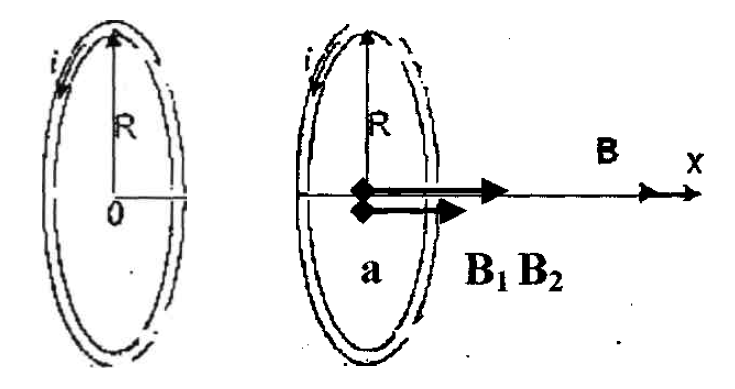 Рис.4. Индукция магнитного поля двух круглых катушек при последовательном согласном их включении. Практическая часть Ход работы:
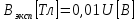 Например: В1эксп=0,01*0,03=0,0003 (Тл) B2эксп=0,01*0,06=0,0006 (Тл) В3эксп=0,01*0,11=0,0011 (Тл) и т.д.
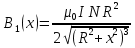 Например: B1(x1)= 4*3,14*10^(-7)*133,9*10^(-3)*250*0,007^2/(2*(0,007^2+(-0,015)^2)^(3/2))=0,000227 (Тл) B2(x2)= 4*3,14*10^(-7)*133,9*10^(-3)*250*0,007^2/(2*(0,007^2+(-0,01)^2)^(3/2))=0,000566 (Тл) B3(x3)= 4*3,14*10^(-7)*133,9*10^(-3)*250*0,007^2/(2*(0,007^2+(-0,005)^2)^(3/2))=0,001618 (Тл) и т.д.
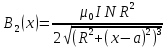 где а=0,03 Например: B1(x1)= 4*3,14*10^(-7)*133,9*10^(-3)*250*0,007^2/(2*(0,007^2+(-0,015-0,03)^2)^(3/2))=0,000011(Тл) B2(x2)= 4*3,14*10^(-7)*133,9*10^(-3)*250*0,007^2/(2*(0,007^2+(-0,01-0,03)^2)^(3/2))=0,000015 (Тл) B3(x3)= 4*3,14*10^(-7)*133,9*10^(-3)*250*0,007^2/(2*(0,007^2+(-0,005-0,03)^2)^(3/2))=0,000023 (Тл) и т.д.
Bтеор=B1(x)+B2(x) Например: Втеор1=0,000227+0,000011=0,00001587 (Тл) Втеор2=0,000566 +0,000015 =0,0000214 (Тл) Втеор3=0,001618 +0,000023 =0,0000299 (Тл)
I=133,9мА=0,1339А
Провел повторные исследования, установив катушки последовательном встречном включении: 1) Провела аналогичные расчеты по тем же формулам и получил следующие результаты: I=149,7мА=0,1497А а=0,03
2) График зависимости Вэксп и Bтеор от X Вывод: 1) При последовательном согласном включении: При плавном смещении датчика Холла (шаг равен 5мм) нашла экспериментальное значение магнитной индукции кольцевой катушки. Построила график зависимости Вэксп и Bтеор от X. Вначале (от 0 до 0,03м) графики представлены в виде параболы, что указывает на одинаковое направление тока в катушках - выполняется принцип суперпозиций. Вследствие неточности проведения исследования, второй пик на графике Вэксп получился со смешением от Bтеор на 2-3мм. 2) При последовательном встречном включении: Провела повторное исследование. Построила график зависимости Вэксп и Bтеор от X. При последовательном встречном включении графики имеют схожую форму (смещение от Bтеор на 1-2мм) – параболу. Но в отличие от первого случая парабола приходится на конец графика (от 0,035 до 0,065м). Следовательно ток течет в противоположном направлении – принцип суперпозиции выполняется. |
