отчёт 4. Лабораторная работа 4 исследование решения систем линейных алгебраических уравнений (слау) методом гаусса

Название	Лабораторная работа 4 исследование решения систем линейных алгебраических уравнений (слау) методом гаусса
Анкор	отчёт 4.docx
Дата	15.08.2018
Размер	331.88 Kb.
Формат файла
Имя файла	отчёт 4.docx
Тип	Лабораторная работа #22994

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ

БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«ВЯТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»

Лабораторная работа №4

ИССЛЕДОВАНИЕ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ (СЛАУ) МЕТОДОМ ГАУССА

Вариант №5

Студент: гр. УТ – 21 Петухов П.А.

Преподаватель: Чуркин В.В.

Киров

2013 год

1.Задание.

Решить СЛАУ в Mathcad’е.
Составить алгоритм и написать код для решения СЛАУ методом Гаусса с частичным выбором ведущего коэффициента по столбцу
Получить зависимости временных затрат от размера системы и усредненной точности решения от размера системы и типа представления (float, double, longdouble) коэффициентов.

2.Формулы.

Методом Гаусса называют точный метод решения невырожденной системы линейных уравнений состоящий в том что последовательным исключением неизвестных систему





приводят к эквивалентной системе с верхней треугольной матрицей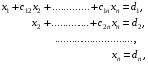

решение которой находят по рекуррентным формулам





Метод Гаусса содержит прямой ход на котором исходную систему преобразуют к треугольному виду и обратный ход на котором решают треугольную систему эквивалентную исходной

3.Решение СЛАУ в Mathcad’е.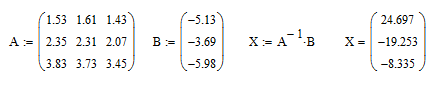

$c:\users\pavel\desktop\безымянный.png$

4.Блок-схемы алгоритмов.

1)Прямой ход алгоритма метода Гаусса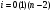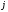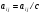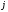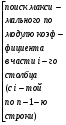

2)Обратный ход

5.Таблица идентификаторов

Имя переменной			Тип переменной	Диапазон	Назначение
Алгоритм		Программа	Тип переменной	Диапазон	Назначение
a1[3][4]		a1[3][4]	float	От -3.4 × 10³⁸ до 3.4 × 10³⁸	Матрица для решения СЛАУ 3-го порядка
с		с	float	-----------//-----------	Для поиска максимального коэффициента
z		z	float	-----------//-----------	Для перестановки элементов
s		s	float	-----------//-----------	Для вычитания строк
x[3]	x[3]		float	-----------//-----------	Матрица столбец искомых переменных
nev	nev		float	-----------//-----------	Расчёт невязки
d	d		float	-----------//-----------	Коэффициент -множитель
b	b		float	-----------//-----------	Коэффициент -множитель
snev_f	snev_f		float	-----------//-----------	невязка (float)*1.0e6
snev_d	snev_d		double	От ±5.0 × 10⁻³²⁴ до ±1.7 × 10³⁰⁸	невязка (double)*1.0e15
snev_ld	snev_ld		long double	От ±5.0 × 10⁻³²⁴ до ±1.7 × 10³⁰⁸	невязка (long double)*1.0e18
i	i		int	От -2 147 483 648 до 2 147 483 647	Переменная цикла
j	j		int	-----------//-----------	Переменная цикла
k	k		int	-----------//-----------	Переменная цикла
k	k		int	-----------//-----------	Кол-во СЛАУ
l	l		int	-----------//-----------	Переменная цикла
n	n		int	-----------//-----------	Переменная цикла
mul	mul		int	-----------//-----------	Счётчик числа делений/умнож.
smul	smul		int	-----------//-----------	Сумма делений/умножений
ad	ad		int	-----------//-----------	Счётчик числа сложений/вычитаний
sad	sad		int	-----------//-----------	Сумма сложений/вычитаний
max	max		int	-----------//-----------	Индекс максимального элемента

6.Код программы
Содержание модуля Class1.cpp

//---------------------------------------------------------------------------

#pragma hdrstop

#include "Class1.h"

#include "string.h"

#include "strstream.h"

#include "Unit1.h"

#include "Unit2.h"

#include "Unit3.h"

#include "Unit4.h"

#include

//---------------------------------------------------------------------------

#pragma package(smart_init)

#pragma link "CSPIN"

//#pragma resource "*.dfm"
void Class1::aboutme()

{

Application->MessageBox("Данное приложение выполнено студентом ВятГУ Факультета АВТ группы УТ-21 Петуховым Павлом", "О создателе" );

}

const int n=3;

const float a[][4]={{1.53,1.61,1.43,-5.13},{2.35,2.31,2.07,-3.69},

{3.83,3.73,3.45,-5.98}};

float x[3];
void Class1::test_SLAU_3()

{

AnsiString s;

for(int j=0;j<3;j++){

if(j<2)s=" + ";

else s="";

for(int i=0;i<3;i++){

Form1->StringGrid1->Cells[2*j][i]=FloatToStrF(a[i][j],ffFixed,5,2)

+" * ";

Form1->StringGrid1->Cells[2*j+1][i]=" x["+IntToStr(j)+"]"+s;}

for(int i=0;i<3;i++){

Form1->StringGrid1->Cells[6][i]=" = ";

Form1->StringGrid1->Cells[7][i]=FloatToStrF(a[i][3],ffFixed,5,2);}}

}

void Class1::gauss(float& nev,int& mul,int& ad)

{

int i,j,k,l;

float a1[3][4],c,b,s;

//копирование исходной матрицы во вспомогательную матрицу

for(i=0;i
for(j=0;j
//решение СЛАУ

mul=ad=0;

for(i=0;i
c=a1[i][i];

for(j=i;j
for(k=i+1;k
b=a1[k][i];

for(l=i;l
{a1[k][l]-=b*a1[i][l]; ad++; mul++;}}}

x[n-1]=a1[n-1][n]/a1[n-1][n-1]; mul++;

for(k=n-2;k>=0;k--){

s=0;

for(j=k+1;j
{s+=a1[k][j]*x[j]; ad++; mul++;}

x[k]=a1[k][n]-s; ad++;}

//вычисление невязки

c=0;

for(int i=0;i
b=0;

for(int j=0;j
c+=pow(b-a[i][n],2);}

nev=sqrt(c)/n;

}

void Class1::helpf()

{

Form3->Show(); //обращение к форме

}

void Class1::resh()

{

int mul,ad;

float nev;

gauss(nev,mul,ad);

for(int i=0;i<3;i++){

Form1->StringGrid2->Cells[0][i]=" x["+IntToStr(i)+"] = ";

Form1->StringGrid2->Cells[1][i]=FloatToStrF(x[i],ffFixed,7,5);}

Form1->LabeledEdit1->Text=FloatToStrF(nev,ffExponent,4,2);

Form1->LabeledEdit2->Text=IntToStr(mul);

Form1->LabeledEdit3->Text=IntToStr(ad);}

void Class1::test_SLAU_n()

{

Form2->Show();

Form2->StringGrid1->Cells[0][0]=" n";

Form2->StringGrid1->Cells[1][0]=" k";

Form2->StringGrid1->Cells[2][0]=" mul";

Form2->StringGrid1->Cells[3][0]=" ad";

Form2->StringGrid1->Cells[4][0]=" nev_f";

Form2->StringGrid1->Cells[5][0]=" nev_d";

Form2->StringGrid1->Cells[6][0]=" nev_ld";

}

template

void Class1::gauss_1(float**b,int n,T& nev,int& mul,int& ad)

{ T c,z,d,s;

int max;

T* x=new T[n];

T** a=new T*[n];

for(int i=0;i
for(int i=0;i
for(int j=0;j
a[i][j]=b[i][j];

mul=ad=0;

for(int i=0;i
max=i;

for(int k=i+1;k
if(fabs(a[k][i])>fabs(a[max][i])) max=k;

for(int j=i;j
{z=a[i][j]; a[i][j]=a[max][j]; a[max][j]=z;}

c=a[i][i];

for(int j=i;j
for(int k=i+1;k
d=a[k][i];

for(int l=i;l
{a[k][l]-=d*a[i][l]; mul++; ad++;}}}

x[n-1]=a[n-1][n]/a[n-1][n-1]; mul++;

for(int k=n-2;k>=0;k--){

s=0;

for(int j=k+1;j
x[k]=a[k][n]-s; ad++;}

//вычисление невязки

c=0;

for(int i=0;i
d=0;

for(int j=0;j
c+=pow(d-b[i][n],2);}

nev=sqrt(c)/n;

for(int i=0;i
delete[]a; a=0;

delete[]x; x=0;

}

//---------------------------------------------------------------------------

int pk=1;

//---------------------------------------------------------------------------

void Class1::resh1()

{

Form4->Series1->Clear();

Form4->Series2->Clear();

Form4->Series3->Clear();

Form4->Series4->Clear();

Form4->Series5->Clear();

int count=0, current=0;

for(int n=Form2->CSpinEdit1->Value; n<=Form2->CSpinEdit2->Value;

n+=Form2->CSpinEdit3->Value)

count+=n; count*=Form2->CSpinEdit4->Value;

float**b,w,z;

int mul,smul,ad,sad;

float nev_f,snev_f;

double nev_d,snev_d;

long double nev_ld,snev_ld;

int k=Form2->CSpinEdit4->Value;

for(int n=Form2->CSpinEdit1->Value;

n<=Form2->CSpinEdit2->Value;n+=Form2->CSpinEdit3->Value){

b=new float*[n];

for(int i=0;i
b[i]=new float[n+1];

smul=0; sad=0; snev_f=0; snev_d=0; snev_ld=0;

for(int kc=0;kc
srand(time(NULL));

for(int i=0;i
w=rand()%(Form2->CSpinEdit7->Value-Form2->CSpinEdit8->Value+1)+Form2->CSpinEdit8->Value

+(float)random(Form2->CSpinEdit7->Value-Form2->CSpinEdit8->Value+1)

/(Form2->CSpinEdit7->Value-Form2->CSpinEdit8->Value)-0.5;

if(w>Form2->CSpinEdit7->Value)w=Form2->CSpinEdit7->Value;

if(wCSpinEdit8->Value)w=Form2->CSpinEdit8->Value;

b[i][n]=w;

for(int j=0;j
z=rand()%(Form2->CSpinEdit5->Value-Form2->CSpinEdit6->Value+1)+Form2->CSpinEdit6->Value

+(float)random(Form2->CSpinEdit5->Value-Form2->CSpinEdit6->Value+1)

/(Form2->CSpinEdit5->Value-Form2->CSpinEdit6->Value)-0.5;

if(z>Form2->CSpinEdit5->Value)z=Form2->CSpinEdit5->Value;

if(zCSpinEdit6->Value)z=Form2->CSpinEdit6->Value;

b[i][j]=z; }}

gauss_1(b,n,nev_f,mul,ad);

snev_f+=nev_f; smul+=mul; sad+=ad;

gauss_1(b,n,nev_d,mul,ad);

snev_d+=nev_d;

gauss_1(b,n,nev_ld,mul,ad);

snev_ld+=nev_ld;

current+=n;

Form2->ProgressBar1->Position=100*current/count; }

Form2->StringGrid1->Cells[0][pk]=IntToStr(n);

Form2->StringGrid1->Cells[1][pk]=IntToStr(k);

Form2->StringGrid1->Cells[2][pk]=IntToStr(smul);

Form2->StringGrid1->Cells[3][pk]=IntToStr(sad);

Form2->StringGrid1->Cells[4][pk]=FloatToStrF(snev_f/k,ffExponent,5,4);

Form2->StringGrid1->Cells[5][pk]=FloatToStrF(snev_d/k,ffExponent,5,4);

Form2->StringGrid1->Cells[6][pk]=FloatToStrF(snev_ld/k,ffExponent,5,4);

Form4->Series1->AddXY(n,smul,"",clRed);

Form4->Series2->AddXY(n,sad,"",clGreen);

Form4->Series3->AddXY(n,snev_f/k*1.0e6,"",clRed);

Form4->Series4->AddXY(n,snev_d/k*1.0e15,"",clGreen);

Form4->Series5->AddXY(n,snev_ld/k*1.0e18,"",clBlack);

pk++;

for(int i=0;i
delete[]b; b=0; }

}
void Class1::graf()

{

Form4->Show();

}
void Class1::sbros()

{

for(int i=1;iStringGrid1->RowCount;i++)

for(int j=0;jStringGrid1->ColCount;j++)

Form2->StringGrid1->Cells[j][i]="";

Form2->ProgressBar1->Position=0;

Form4->Series1->Clear();

Form4->Series2->Clear();

Form4->Series3->Clear();

Form4->Series4->Clear();

Form4->Series5->Clear();

pk=1;

}
7.Результаты выполнения работы в виде таблиц и графиков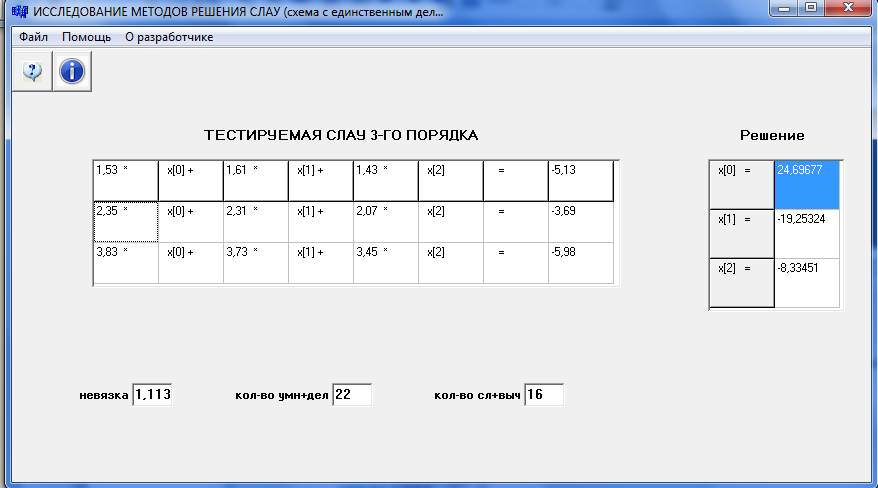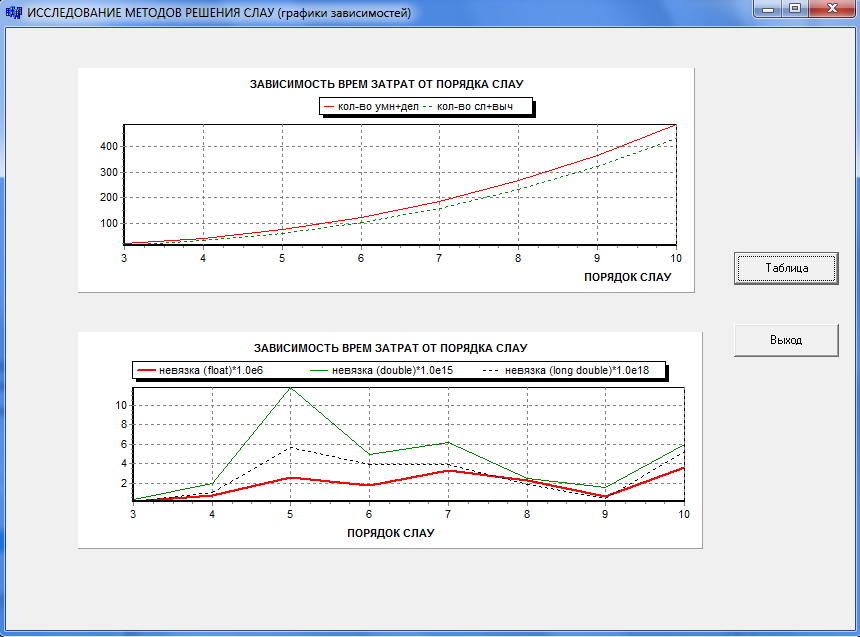

$c:\users\pavel\desktop\3.png$

$c:\users\pavel\desktop\2.png$

$c:\users\pavel\desktop\4.png$

8.Библиографический список.

В.В.ЧУРКИН ЧИСЛЕННЫЕ МЕТОДЫ (с алгоритмами и программами в среде C++Builder) Учебно-методическое пособие. 2013.