Сборник лаб-работ. Работа-4. Лабораторная работа 4 Исследование спектрального анализа и синтеза периодических сигналов Методические указания и задания
 Скачать 1.33 Mb. Скачать 1.33 Mb.
|
 Федеральное агентство связи Ордена Трудового Красного Знамени федерального государственного бюджетного образовательного учреждения высшего образования «Московский технический университет связи и информатики» Волго-Вятский филиал Кафедра инфокоммуникационных и общепрофессиональных дисциплин (ИКиОПД) Общая теория связи Лабораторная работа № 4 «Исследование спектрального анализа и синтеза периодических сигналов» Методические указания и задания Выполнил: Проверил: Чернявский А.Д. Нижний Новгород 2021 Цель работы. Приобретение навыков спектрального анализа и синтеза периодических сигналов. Теоретическая часть В общем случае периодический сигнал s(t) описывается соотношением где T – постоянная величина, называемая периодом, с; n – любое целое число (положительное или отрицательное). Периодический сигнал s(t) может быть разложен в ряд Фурье. Чтобы такое разложение существовало, фрагмент сигнала s(t) длительностью в один период должен удовлетворять условиям Дирихле: не должно быть разрывов второго рода (с уходящими в бесконечность ветвями функции); число разрывов первого рода (скачков) должно быть конечным; число экстремумов должно быть конечным (в качестве примера функции, которая на конечном интервале имеет бесконечное число экстремумов, можно привести sin(l/x) в окрестности нуля). Различают три формы записи ряда Фурье: синусно-косинусная форма, вещественная форма и комплексная форма. Синусно-косинусная форма ряда Фурье имеет следующий вид: где k = 1, 2, …, ∞ – номер гармоники спектра Фурье периодического сигнала; ω1 = 2π/T – основная круговая частота периодического сигнала (частота первой гармоники), рад/с; kω1 – круговая частота k-й гармоники, рад/с; 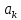 – коэффициент k-й «косинусной» составляющей спектра Фурье – коэффициент k-й «косинусной» составляющей спектра Фурьепериодического сигнала, В; 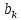 – коэффициент k-й «синусной» составляющей спектра Фурье периодического сигнала, В; – коэффициент k-й «синусной» составляющей спектра Фурье периодического сигнала, В;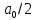 – постоянная составляющая спектра Фурье периодического – постоянная составляющая спектра Фурье периодическогосигнала, представляющая собой среднее значение сигнала на периоде, В. Использованные в (2.2) коэффициенты 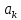 , ,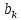 (k = 1, 2, …, ∞) и (k = 1, 2, …, ∞) и 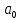 определяются по формулам: определяются по формулам: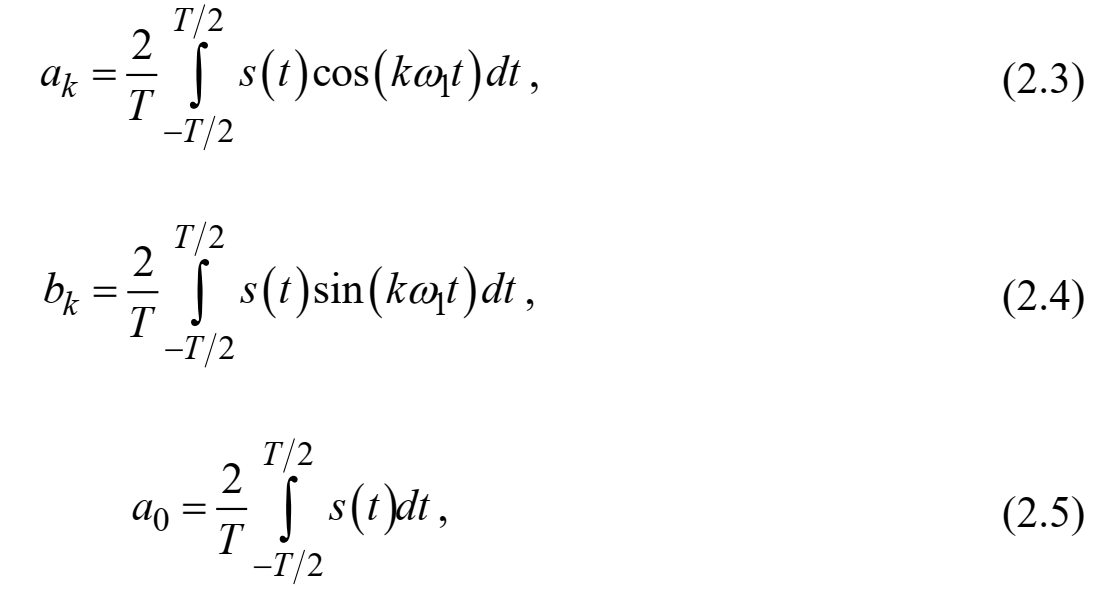 Примечание – Пределы интегрирования в формулах (2.3) – (2.5) не обязательно должны быть от –T/2 до T/2. Интегрирование может производиться по любому интервалу длиной T, результат от этого не изменится. Конкретные пределы выбираются из соображений удобства вычислений; например, может оказаться удобнее выполнять интегрирование от 0 до T или от – T до 0. На основе анализа (2.2) видно, что базисные функции синусно-косинусной формы ряда Фурье можно представить в виде: 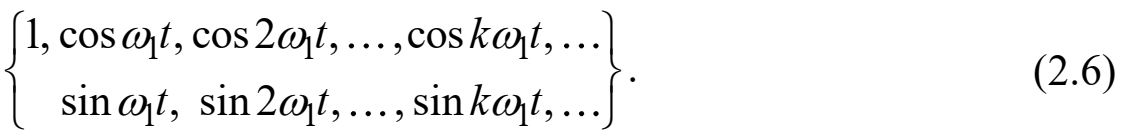 Примечание – Все функции системы (2.6) попарно ортогональны на интервале (–T/2; T/2) или (0; T), а частоты косинусоидальных и синусоидальных составляющих образуют арифметическую прогрессию. Таким образом, в общем случае спектр периодического сигнала s(t) при использовании синусно-косинусной формы ряда Фурье состоит из постоянной составляющей 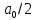 и бесконечного множеств коэффициентов {ak}, {bk} (k = 1, 2, …, ∞) при «косинусных» и «синусных» составляющих спектра. и бесконечного множеств коэффициентов {ak}, {bk} (k = 1, 2, …, ∞) при «косинусных» и «синусных» составляющих спектра.В частном случае, если сигнал s(t) является четной функцией, то все коэффициенты 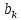 будут равны нулю и, в формуле ряда Фурье будут присутствовать только «косинусные» слагаемые. будут равны нулю и, в формуле ряда Фурье будут присутствовать только «косинусные» слагаемые.Если сигнал s(t) является нечетной функцией, равны нулю будут, наоборот, косинусные коэффициенты 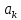 , и в формуле останутся лишь «синусные» слагаемые. , и в формуле останутся лишь «синусные» слагаемые.Некоторое неудобство синусно-косинусной формы ряда Фурье состоит в том, что для каждого значения индекса суммирования k в формуле (2.2) фигурируют два слагаемых – синус и косинус. Поскольку справедливо соотношение: где 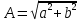 – амплитуда гармонического сигнала, В; – амплитуда гармонического сигнала, В; 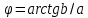 – начальная фаза гармонического сигнала, радианы или градусы, то ряд (2.2) можно также представить в компактной форме: – начальная фаза гармонического сигнала, радианы или градусы, то ряд (2.2) можно также представить в компактной форме: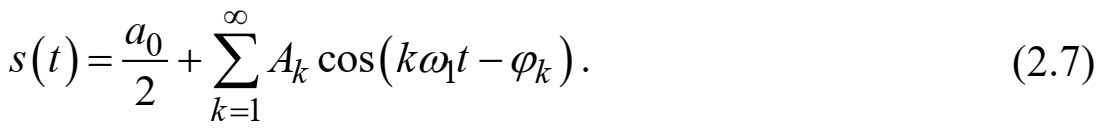 Формула (2.7) представляет вещественную форму записи ряда Фурье. Если сигнал s(t) является четной функцией, фазы 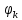 могут принимать только значения 0 и π, а если s(t) – функция нечетная, то возможные значения для фазы равны ±π/2. могут принимать только значения 0 и π, а если s(t) – функция нечетная, то возможные значения для фазы равны ±π/2.Обратный переход от вещественной к синусно-косинусной форме записи ряда Фурье осуществляется на основе соотношений: Сравнивая между собой вещественную к синусно-косинусную форму записи ряда Фурье, отметим, что: - при использовании синусно-косинусной формы разложения периодического сигнала в тригонометрический ряд (2.2) коэффициенты 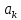 и и 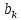 зависят от выбора начала отсчета, а при пользовании вещественной формы разложения (2.7) амплитуды гармоник Ak не зависят от выбора начала отсчета и определяются только видом сигнала s(t), а аргументы гармоник зависят от выбора начала отсчета, а при пользовании вещественной формы разложения (2.7) амплитуды гармоник Ak не зависят от выбора начала отсчета и определяются только видом сигнала s(t), а аргументы гармоник 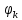 зависят от начала отсчета при выборе пределов интегрирования в формулах (2.3) – (2.5); зависят от начала отсчета при выборе пределов интегрирования в формулах (2.3) – (2.5);- при сдвиге начала отсчета вдоль оси времени t на 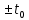 амплитуды Ak сохраняются, а фазы амплитуды Ak сохраняются, а фазы 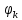 получают приращение получают приращение 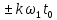 (теорема сдвига). (теорема сдвига).Комплексная форма представления ряда Фурье является наиболее общей и получается из вещественной формы представлением косинуса в виде полусуммы комплексных экспонент (такое представление вытекает из формулы Эйлера) 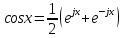 Применив данное преобразование к вещественной форме ряда Фурье, получим суммы комплексных экспонент с положительными и отрицательными показателями: Будем трактовать экспоненты со знаком «минус» в показателе как члены ряда с отрицательными номерами. В рамках этого же общего подхода постоянное слагаемое 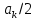 станет членом ряда с нулевым номером. В результате получится комплексная форма записи ряда Фурье: станет членом ряда с нулевым номером. В результате получится комплексная форма записи ряда Фурье:Комплексные коэффициенты ряда 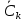 связаны с амплитудами Ak и фазами связаны с амплитудами Ak и фазами 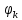 , фигурирующими в вещественной форме записи ряда Фурье (2.7), следующими соотношениями: , фигурирующими в вещественной форме записи ряда Фурье (2.7), следующими соотношениями:Несложно выглядят и формулы связи 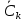 с коэффициентами с коэффициентами 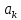 и и 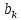 синусно-косинусной формы ряда Фурье (2.2): синусно-косинусной формы ряда Фурье (2.2):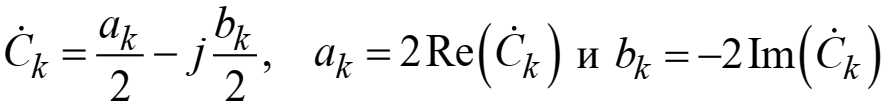 Отсюда сразу же следует и формула непосредственного расчета коэффициентов 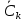 ряда Фурье в комплексной форме: ряда Фурье в комплексной форме: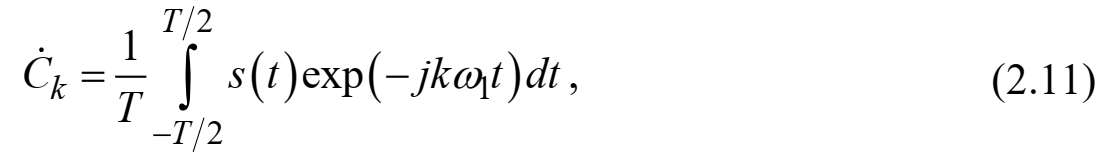 где k – любое целое число. Формула (2.11) определяет комплексный спектр периодического сигнала. Если s(t) является четной функцией, коэффициенты ряда 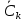 будут чисто вещественными, а если s(t) – функция нечетная, коэффициенты ряда окажутся чисто мнимыми. будут чисто вещественными, а если s(t) – функция нечетная, коэффициенты ряда окажутся чисто мнимыми.Совокупность амплитуд гармоник ряда Фурье часто называют амплитудным спектром периодического сигнала (спектр), а совокупность их фаз – фазовым спектром периодического сигнала (таблица 2.1).   Если анализируемый сигнал s(t) является вещественным, то его амплитудный и фазовый спектры обладают соответственно четной и нечетной симметрией: а коэффициенты комплексного ряда Фурье – комплексно-сопряженной симметрией: где * – символ математической операции комплексного сопряжения. Спектральной диаграммой периодического сигнала принято называть графическое изображение коэффициентов ряда Фурье для заданного сигнала. Различают амплитудные и фазовые спектральные диаграммы (рисунки 2.1 и 2.2). Сформулируем основные свойства спектральных диаграмм периодических сигналов: - первое свойство спектров, изображенных на рисунках 2.1 и 2.2, состоит в том, спектральные диаграммы периодического сигнала являются дискретными функциями частоты, поэтому их называют также линейчатым. - второе свойство спектров, изображенных на рисунках 2.1 и 2.2, состоит в том, что эти спектры являются гармоническими. Это значит, что они состоит из равноотстоящих спектральных линий, т. к. частоты гармоник находятся в простых кратных соотношениях (все гармоники спектра имеют частоты 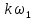 кратные частоте первой гармоники кратные частоте первой гармоники 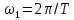 ). ).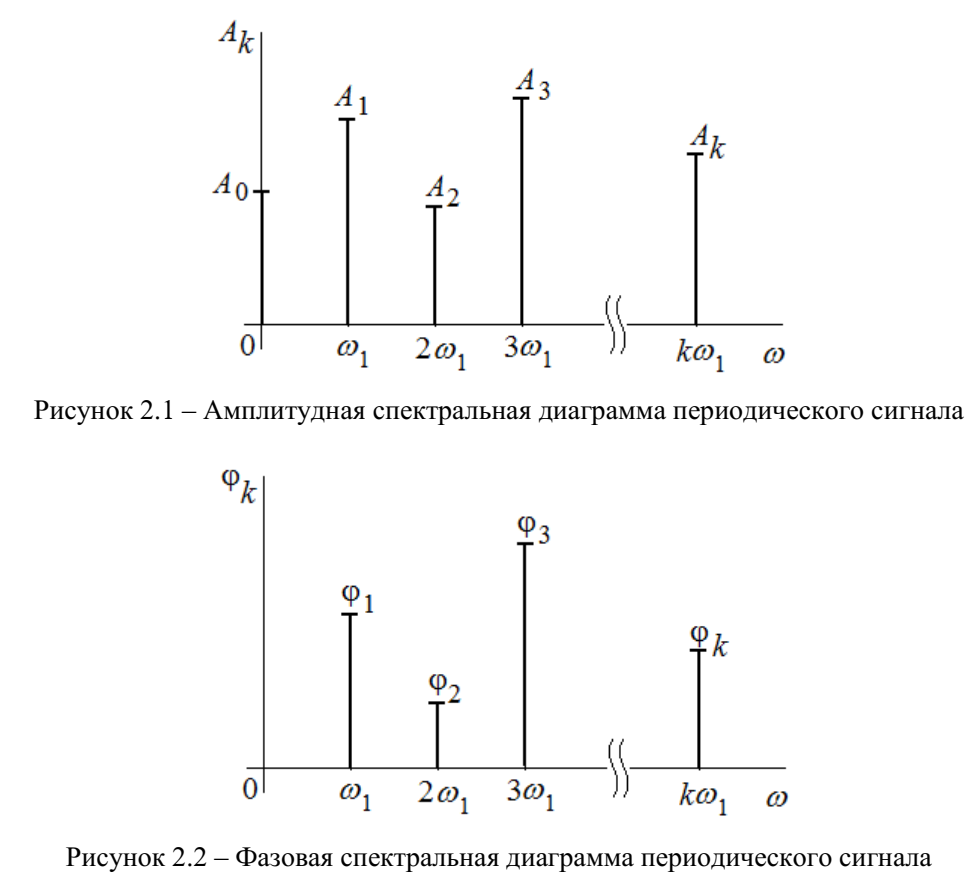 Примечание – Конечно, отдельные гармоники, иногда даже первая, могут отсутствовать, т. е. амплитуды их могут равняться нулю, но это, однако, не нарушает гармоничности спектра. Итак, ряд Фурье представляет данный периодический сигнал s(t) суммой гармонических колебаний (синусоид и косинусоид) кратных частот с соответствующим образом подобранными амплитудами и фазами. Если ограничится конечным числом членов ряда (2.2) и (2.7), то получим периодический сигнал 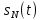 являющийся приближенным изображением сигнала являющийся приближенным изображением сигнала 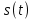 : :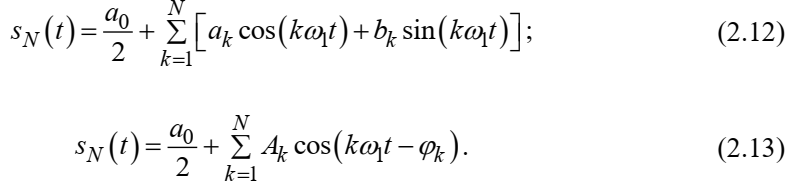 С увеличением числа членов N приближение, разумеется, улучшается, и в пределе, при 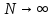 приближенные равенства (2.12) и (2.13) переходят в точные (2.2) и (2.7), соответственно. приближенные равенства (2.12) и (2.13) переходят в точные (2.2) и (2.7), соответственно.При этом существенно, что приближения (2.12) и (2.13) есть всегда наилучшие приближения для любого N, т. е. когда возникает необходимость аппроксимировать периодическую функцию тригонометрическим полиномом, то наименьшее квадратичное отклонение получится, если коэффициенты полинома будут определены по формулам (2.3) – (2.5). Известно, что если существует интеграл 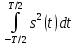 , то средняя квадратическая погрешность , то средняя квадратическая погрешность 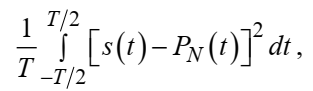 где 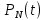 – произвольный тригонометрический многочлен вида – произвольный тригонометрический многочлен вида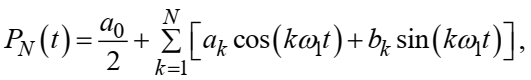 при каждом N принимает наименьшее значение, когда в качестве коэффициентов 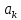 и и 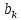 многочлена многочлена 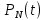 берутся соответствующие коэффициенты Фурье (2.3) – (2.5) берутся соответствующие коэффициенты Фурье (2.3) – (2.5) 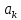 и и 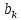 функции s(t), т. е. когда тригонометрический многочлен функции s(t), т. е. когда тригонометрический многочлен 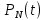 есть частичная сумма есть частичная суммаряда Фурье функции s(t) . Следует учитывать, что при усечении рядов Фурье определенное искажение функций существует всегда. Но при малой доле энергии отсекаемой части сигнала (при быстром затухании спектров функций с ростом номера гармоники) этот эффект, получивший название эффекта Гиббса, может быть и малозаметен. На скачках и разрывах функций эффект Гиббса проявляется наиболее ярко, что может весьма существенно сказаться на качестве и точности обработки сигналов: - крутизна перепадов «размывается», т. к. она не может быть больше, чем крутизна (в нулевой точке) последней сохраненной гармоники ряда (2.12) или (2.13); - по обе стороны «размытых» перепадов появляются выбросы и затухающие осцилляции с частотой, равной частоте последнего сохраненного или первого отброшенного члена ряда (2.12) или (2.13). Более подробно проявление эффекта Гиббса будет рассмотрено далее в примере спектрального анализа и синтеза периодической последовательности прямоугольных импульсов. Теорема Парсеваля. Определив среднюю мощность сигнала s(t), представленного в виде ряда Фурье (2.2), за период колебаний T, получим: 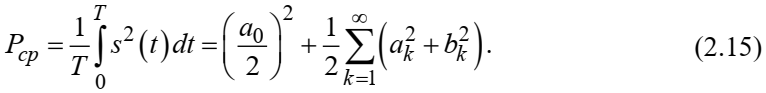 При выводе формулы (2.15) использовано соотношение 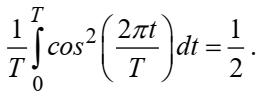 Соотношение (2.15) представляет собой математическую запись теоремы Парсеваля, из которой следует, что если периодический сигнал s(t)разлагается в ряд Фурье, то средняя за период мощность этого сигнала заключается в сумме мощностей постоянной составляющей и гармоник спектра Фурье. При использовании вещественной формы записи ряда Фурье (2.7) равенство Парсеваля (2.15) можно, также переписать в виде 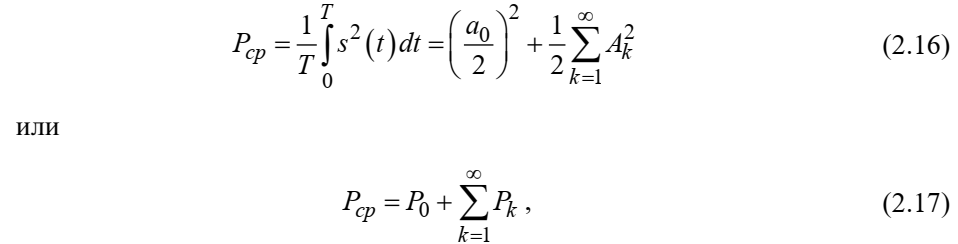  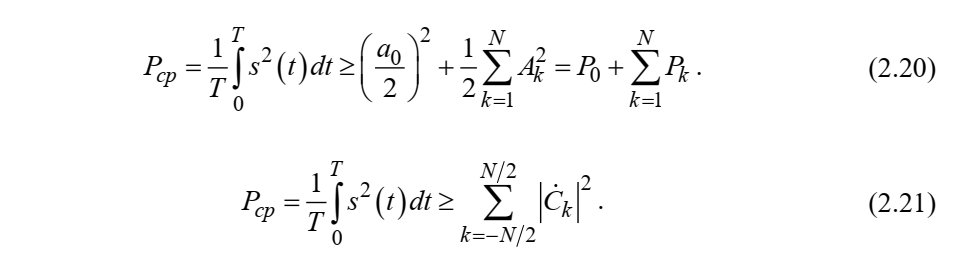 Оборудование и материалы Для выполнения лабораторной работы необходим персональный компьютер. Также необходима операционная система WINDOWS , программа MathCAD 13 и выше. Указания по технике безопасности При выполнении лабораторной работы запрещается: - самостоятельно производить ремонт персонального компьютера, а также установку и удаление имеющегося программного обеспечения; - нарушать общепринятые правила техники безопасности при работе с электрооборудованием, в частности, касаться электрических розеток металлическими предметами и т.д.; - принимать пищу, напитки и сорить на рабочем месте пользователя персонального компьютера. В случае неисправности персонального компьютера необходимо немедленно сообщить об этом обслуживающему персоналу лаборатории (системному администратору, оператору). Указания по порядку выполнения работы Методику выполнения работы рассмотрим на примере спектрального анализа и синтеза в усеченном базисе Фурье (ограничиться рассмотрением десяти гармоник т. е. N =10) периодической последовательности прямоугольных импульсов с высотой A = 1 В, длительностью τ = 0,2 с и периодом Т = 1 с (рисунок 2.3). 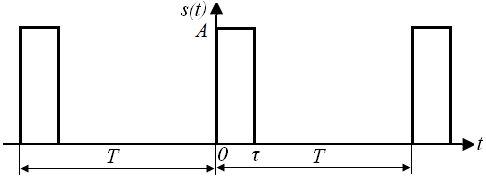 Рис.2.3. Периодическая последовательность прямоугольных импульсов Требуется для сигнала s(t) определить:  – основную круговую частоту периодического сигнала (частоту первой гармоники), рад/с; – основную круговую частоту периодического сигнала (частоту первой гармоники), рад/с;  – коэффициент k-той косинусной составляющей спектра Фурье периодического сигнала, В; – коэффициент k-той косинусной составляющей спектра Фурье периодического сигнала, В; 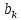 – коэффициент k-той синусной составляющей спектра Фурье периодического сигнала, В; – коэффициент k-той синусной составляющей спектра Фурье периодического сигнала, В; 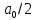 – постоянную составляющую спектра Фурье периодического сигнала, В; – постоянную составляющую спектра Фурье периодического сигнала, В; 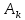 – амплитуду k-той гармоники спектра Фурье периодического сигнала, В; – амплитуду k-той гармоники спектра Фурье периодического сигнала, В; 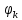 – начальную фазу k-той гармоники спектра Фурье периодического сигнала, радианы или градусы; – начальную фазу k-той гармоники спектра Фурье периодического сигнала, радианы или градусы;- амплитудную и фазовую спектральные диаграммы периодического сигнала (построить линейчатые спектры); - восстановленный по усеченному ряду Фурье сигнал 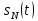 являющийся приближенным изображением сигнала s(t); являющийся приближенным изображением сигнала s(t);- расстояние и квадрат расстояния между сигналами 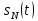 и s(t) за период колебаний T, выраженный в процентной мере относительно квадрата нормы сигнала s(t); и s(t) за период колебаний T, выраженный в процентной мере относительно квадрата нормы сигнала s(t);- среднюю мощность сигнала s(t) за период колебаний T; - сумму мощностей постоянной составляющей и гармоник спектра Фурье, 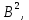 и выполнение неравенства Парсеваля; и выполнение неравенства Парсеваля;- tm – момент времени, когда восстановленный по усеченному ряду Фурье сигнал 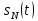 принимает максимальное значение (исследование эффекта Гиббса), с; принимает максимальное значение (исследование эффекта Гиббса), с;- Δ – максимальное значение абсолютной ошибки восстановления сигнала, обусловленное наличием эффекта Гиббса, В; - Δ% – максимальное значение относительной ошибки восстановления сигнала, выраженное в процентах, обусловленное наличием эффекта Гиббса; - исследовать, как влияет изменение количества гармоник усеченного ряда Фурье на изменение параметров эффекта Гиббса – tm, Δ и Δ%. Рассмотрим решение поставленной задачи в математическом пакете Mathcad. В приводимом ниже документе Mathcad приняты следующие обозначения: - s(t) – функция, описывающая зависимость отдельного импульса, составляющего периодическую последовательность импульсов, от текущего времени в пределах одного периода T; - sN(t) – периодическая функция, восстановленная (спектральный синтез) по результатам спектрального анализа (разложению в ряд Фурье) функции s(t) по N гармоникам; - T – период, с; - τ – длительность импульсов, с; - A – высота импульса, В; - N – число рассчитываемых гармоник спектра периодической последовательности импульсов (задача спектрального анализа); - 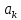 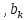 , – коэффициент k-той косинусной и синусной составляющей спектра Фурье периодического сигнала (формула (2.2)), k = 1, 2, 3, ... , N; , – коэффициент k-той косинусной и синусной составляющей спектра Фурье периодического сигнала (формула (2.2)), k = 1, 2, 3, ... , N;- 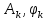 – амплитуда и начальная фаза k-той гармоники спектра Фурье периодического сигнала (формула (2.7)), k = 1, 2, 3, ... , N; – амплитуда и начальная фаза k-той гармоники спектра Фурье периодического сигнала (формула (2.7)), k = 1, 2, 3, ... , N;- 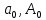 , – удвоенное значение постоянной составляющей спектра Фурье периодического сигнала (формулы (2.2) и (2.7)); , – удвоенное значение постоянной составляющей спектра Фурье периодического сигнала (формулы (2.2) и (2.7));- tm – момент времени, когда восстановленный по усеченному ряду Фурье сигнал sN(t) принимает максимальное значение (исследование эффекта Гиббса); - Δ – максимальное значение абсолютной ошибки восстановления сигнала, обусловленное наличием эффекта Гиббса; - Δ% – максимальное значение относительной ошибки восстановления сигнала, обусловленное наличием эффекта Гиббса; Решение: Запускаем математический пакет Mathcad. Согласно форме сигнала s(t) (таблица 2.3) и заданным параметрам вводим определение сигнала и строим его график в пределах одного периода (рисунок 2.4). 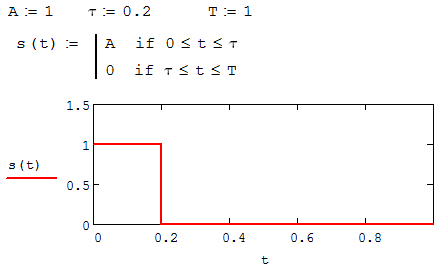 Рисунок 2.4 – Определение и график сигнала s(t) в пределах одного периода 2. Вычисляем основную круговую частоту периодического сигнала (частоту первой гармоники), рад/с, (рисунок 2.5). Рисунок 2.5 – Вычисляем основную круговую частоту периодического сигнала (частоту первой гармоники) Как видно из рисунка 2.5, частота первой гармоники составляет 6,283 рад/с. 3.Задаем количество гармоник усеченного ряда Фурье (N = 10), формируем ранжированную переменную k (k = 0, 1, 2, … , 10) и вычисляем коэффициент 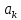 k-той косинусной составляющей спектра Фурье периодического сигнала (рисунок 2.6). k-той косинусной составляющей спектра Фурье периодического сигнала (рисунок 2.6). Рисунок 2.6 – Вычисляем коэффициент k-той косинусной составляющей спектра Фурье периодического сигнала 4. Вычисляем коэффициент 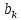 k-той синусной составляющей спектра Фурье периодического сигнала (рисунок 2.7). k-той синусной составляющей спектра Фурье периодического сигнала (рисунок 2.7).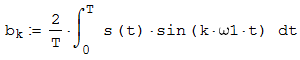 Рисунок 2.7 – Вычисляем коэффициент k-той синусной составляющей спектра Фурье периодического сигнала 5. Отображаем в виде векторов рассчитанные значения коэффициентов 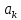 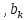 (рисунок 2.8). (рисунок 2.8).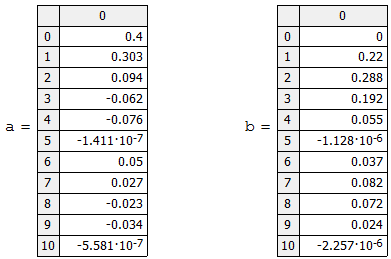 Рисунок 2.8 – Рассчитанные значения коэффициентов 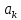 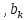 6. Вычисляем постоянную составляющую 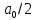 спектра Фурье периодического сигнала (рисунок 2.9). спектра Фурье периодического сигнала (рисунок 2.9).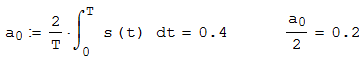 Рисунок 2.9 – Вычисляем постоянную составляющую спектра Фурье периодического сигнала Примечание – Строго говоря, можно было повторно и не вычислять постоянную составляющую спектра Фурье периодического сигнала, т. к. удвоенное значение этой составляющей совпадает со значением элемента вектора a (рисунок) при значении индекса k = 0. 7. Вычисляем и отображаем амплитуды 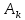 , В, и начальные фазы , В, и начальные фазы 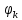 , рад, гармоник спектра Фурье периодического сигнала (рисунок 2.10). , рад, гармоник спектра Фурье периодического сигнала (рисунок 2.10).Примечания - На рисунке 2.10 функция atan2(x,y) возвращает угол, отсчитанный от оси x против хода часовой стрелки до направления на точку с координатами x и y. Результат выражается в радианной мере в диапазоне между –π и π, включая и –π. - При вычислении начальных фаз 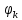 гармоник было использовано ограничение на абсолютную величину k-й синусной составляющей спектра Фурье периодического сигнала гармоник было использовано ограничение на абсолютную величину k-й синусной составляющей спектра Фурье периодического сигнала 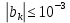 т. к. без этого ограничения, например, для пятой гармоники имеем т. к. без этого ограничения, например, для пятой гармоники имеем 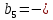 1,128 1,128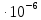 , , 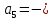 1,411 1,411 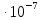 и atan2( и atan2(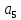 , ,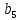 )=-1,659 рад или –97,127 градусов, что является ошибкой. )=-1,659 рад или –97,127 градусов, что является ошибкой. Рисунок 2.10 – Амплитуды и начальные фазы гармоники спектра Фурье периодического сигнала 8. Строим амплитудную и фазовую спектральные диаграммы периодического сигнала (рисунки 2.11 и 2.12). 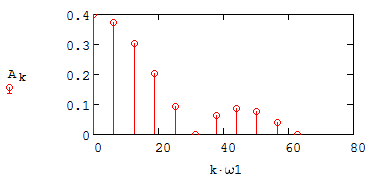 Рисунок 2.11 – Амплитудная спектральная диаграмма периодического сигнала 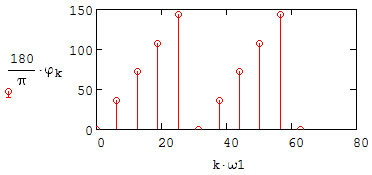 Рисунок 2.12 – Фазовая спектральная диаграмма периодического сигнала Примечания - На рисунках 2.11 и 2.12 вдоль оси абсцисс отложена круговая частота k-й гармоники, рад/с; - На рисунке 2.11 вдоль оси ординат отложена амплитуда k-й гармоники, включая и удвоенное значение постоянной составляющей ( 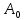 ) спектра Фурье периодического сигнала в вольтах. ) спектра Фурье периодического сигнала в вольтах.- На рисунке 2.12 вдоль оси ординат отложена начальная фаза k-той гармоники спектра Фурье периодического сигнала в градусах. 9. Находим, восстановленный по усеченному ряду Фурье сигнал 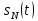 , являющийся приближенным изображением сигнала s(t), и строим его временную диаграмму в пределах двух периодов и временную диаграмму исходного сигнала s(t) в пределах, заданного в пределах одного периода (рисунок 2.13). , являющийся приближенным изображением сигнала s(t), и строим его временную диаграмму в пределах двух периодов и временную диаграмму исходного сигнала s(t) в пределах, заданного в пределах одного периода (рисунок 2.13).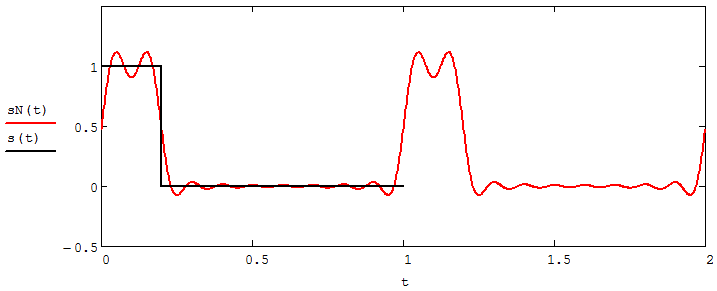 Рисунок 2.13 – Восстановленный по усеченному ряду Фурье сигнал 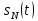 и исходный сигнал s(t), заданный в пределах одного периода и исходный сигнал s(t), заданный в пределах одного периода10. Расстояние и квадрат расстояния между сигналами 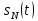 и s(t) за и s(t) запериод колебаний T (рисунок 2.14).  Рисунок 2.14 – Определение расстояния и квадрата расстояния между сигналами 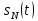 и s(t) и s(t)11. Квадрат расстояния между сигналами 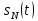 и s(t) за период колебаний T (рисунок 2.15), выраженный в процентной мере относительно квадрата нормы сигнала s(t). и s(t) за период колебаний T (рисунок 2.15), выраженный в процентной мере относительно квадрата нормы сигнала s(t).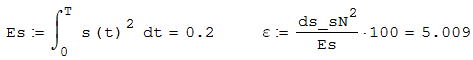 Рисунок 2.15 – Квадрата расстояния между сигналами sN(t ) и s(t ), выраженный в процентной мере относительно квадрата нормы сигнала s(t) Делаем вывод о том, что если ограничиться рассмотрением десяти гармоник спектра Фурье, то квадрат расстояния между сигналами sN(t) и s(t) составляет примерно 5% относительно квадрата нормы сигнала s(t) . 12. Находим среднюю мощность сигнала s(t) за период колебаний T (рисунок 2.16). 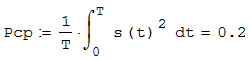 Рисунок 2.16 – Средняя мощность сигнала s(t) за период колебаний T 13. Вычисляем сумму мощностей постоянной составляющей и гармоник спектра Фурье и проверяем выполнение неравенства Парсеваля (рисунок 2.17). 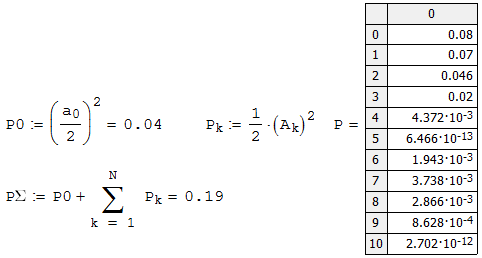 Рисунок 2.17 – Сумма мощностей постоянной составляющей и десяти гармоник спектра Фурье Сравнивая между собой Pcp (рисунок 2.16) и PΣ (рисунок 2.16) убеждаемся в том, что Pcp > PΣ, т. е. неравенство Парсеваля выполняется. 14. Как видно из рисунка 2.13, последовательность прямоугольных импульсов плохо подходит для представления рядом Фурье – она содержит скачки, а сумма любого числа гармонических составляющих с любыми амплитудами всегда будет непрерывной (и более того – бесконечно дифференцируемой во всех точках) функцией. Поэтому поведение ряда Фурье в окрестностях разрывов представляет особый интерес. На временной диаграмме, представленной на рисунке 2.13, хорошо видно, что в окрестности точки разрыва суммирование десяти членов ряда Фурье дает наклонный участок. В самой точке разрыва (в момент времени t = 0) ряд Фурье сходится к полусумме правого и левого пределов: 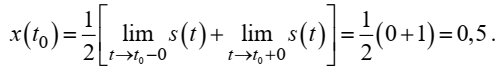 Здесь s(t) – исходный сигнал, sN(t) – сумма усеченного ряда Фурье для него. На примыкающих к разрыву участках сумма усеченного ряда Фурье дает заметные пульсации. Это явление, присущее рядам Фурье для любых сигналов с разрывами первого рода (скачками), как отмечалось ранее, называется эффектом Гиббса. В ряде работ, например, показано, что амплитуда первого (самого большого) выброса составляет примерно 9 % от величины скачка. Убедимся в этом самостоятельно и определим момент времени tm, с, когда восстановленный по усеченному ряду Фурье сигнал  принимает первое после момента времени t = 0 максимальное значение (рисунок 2.18). принимает первое после момента времени t = 0 максимальное значение (рисунок 2.18).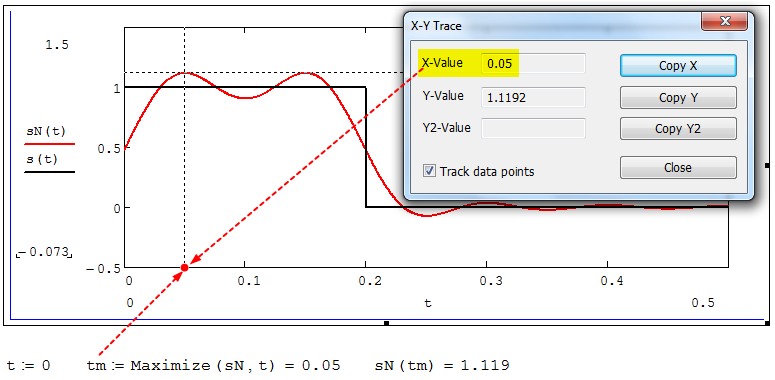 Рисунок 2.18 – Момент времени, когда восстановленный по усеченному ряду Фурье сигнал 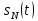 принимает максимальное значение принимает максимальное значениеПримечание – На рисунке 2.18 реализовано два способа определения момента времени tm: - первый способ основан на использовании окна трассировки графика «X-Y Trace»; - второй способ основан на использовании встроенной в Mathcad функции Maximize(f, var1), которая возвращает значение переменной var1 при котором функция f(var1) принимает максимальное значение. Для того, чтобы исключить неоднозначность определения параметра tm (на рисунке 2.18 у функции 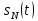 имеется несколько максимумов) перед обращением к функции Maximize(f, var1) задано начальное приближение этого параметра t:= 0, т. е. поиск параметра tm производится в начале системы координат при t равном нулю. имеется несколько максимумов) перед обращением к функции Maximize(f, var1) задано начальное приближение этого параметра t:= 0, т. е. поиск параметра tm производится в начале системы координат при t равном нулю.15. Вычисляем максимальное значение абсолютной ошибки Δ восстановления сигнала, обусловленное наличием эффекта Гиббса (рисунок 2.19). Рисунок 2.19 – Максимальное значение абсолютной ошибки восстановления сигнала, обусловленное наличием эффекта Гиббса 16. Определяем максимальное значение относительной ошибки восстановления сигнала Δ%, обусловленное наличием эффекта Гиббса, выраженное в процентах (рисунок 2.20). Рисунок 2.20 – Максимальное значение относительной ошибки восстановления сигнала, обусловленное наличием эффекта Гиббса, выраженное в процентах Как видно из рисунка 2.20, в рассматриваемом примере, вследствие эффекта Гиббса амплитуда первого (самого большого) выброса составляет примерно 12 % от величины скачка. 17. Исследуем, как повлияет на параметры эффекта Гиббса, изменение количества гармоник спектра сигнала. Увеличим количество гармоник в два и три раза (N = 20 и N = 30). Результат восстановления сигнала и Параметры эффекта Гиббса показаны на рисунках 2.21 и 2.22. 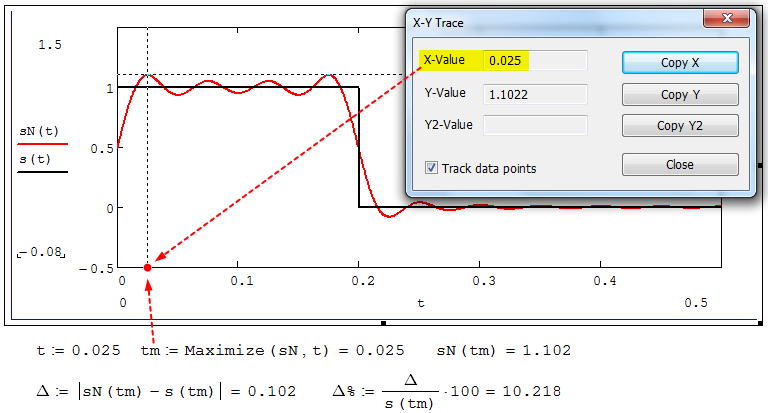 Рисунок 2.21 – Параметры эффекта Гиббса при числе гармоник N = 20 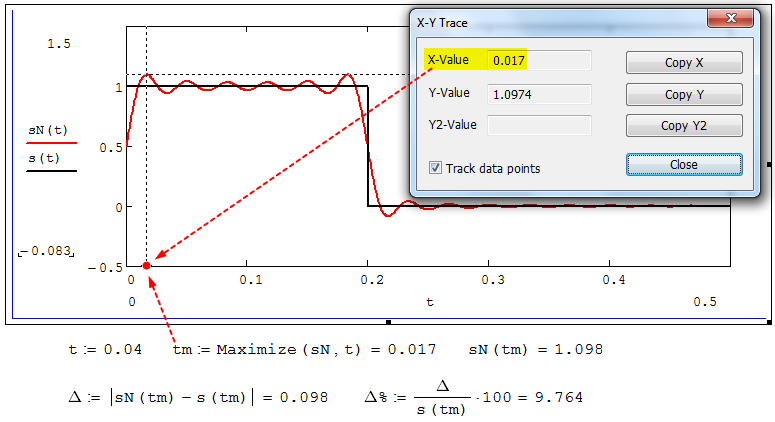 Рисунок 2.22 – Параметры эффекта Гиббса при числе гармоник N = 30 Анализ графика и данных, представленных на рисунках 2.21 и 2.22, свидетельствует о том, что при увеличении количество гармоник в два и три раза (т. е. с 10 до 20 и 30) количество пульсаций восстановленного сигнала тоже удвоилось (утроилось), а амплитуда первого (самого большого) выброса составляет примерно 10 % от величины скачка. Таким образом, исследованный детерминированный, периодический сигнал – периодическая последовательность прямоугольных импульсов (рисунок 2.3) может быть задан функцией s(t) (временной подход) или представлен в виде линейчатого спектра амплитуд и фаз гармоник в базисе Фурье (рисунки 2.11 и 2.12) (спектральный подход). Примечание – В ходе исследования влияния изменение количества гармоник спектра Фурье сигнала на параметры эффекта Гиббса одновременно были исследованы и другие параметры (таблица 2.2). Из анализа данных, приведенных в таблице 2.2 можно сделать выводы о степени влияния изменение количества гармоник спектра Фурье сигнала на качество восстановления по усеченному ряду Фурье сигнала 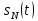 , выполнение неравенства Парсеваля и параметры эффекта Гиббса сигнала , выполнение неравенства Парсеваля и параметры эффекта Гиббса сигнала 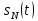 . .Таблица 2.2 – Результаты исследования спектрального анализа и синтеза периодического сигнала 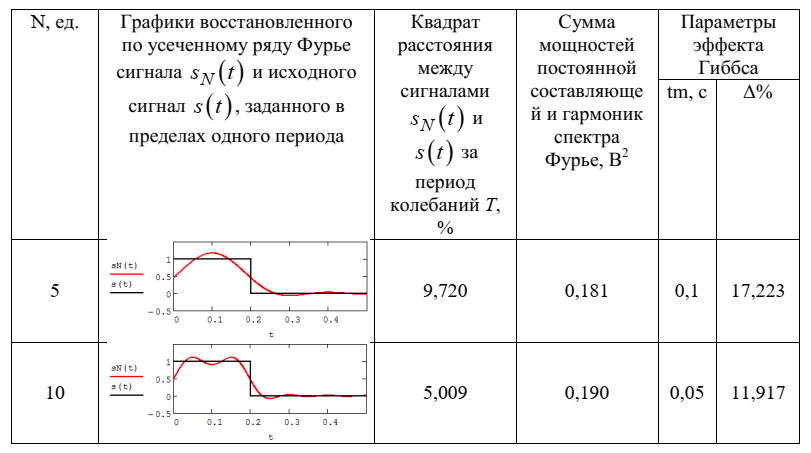 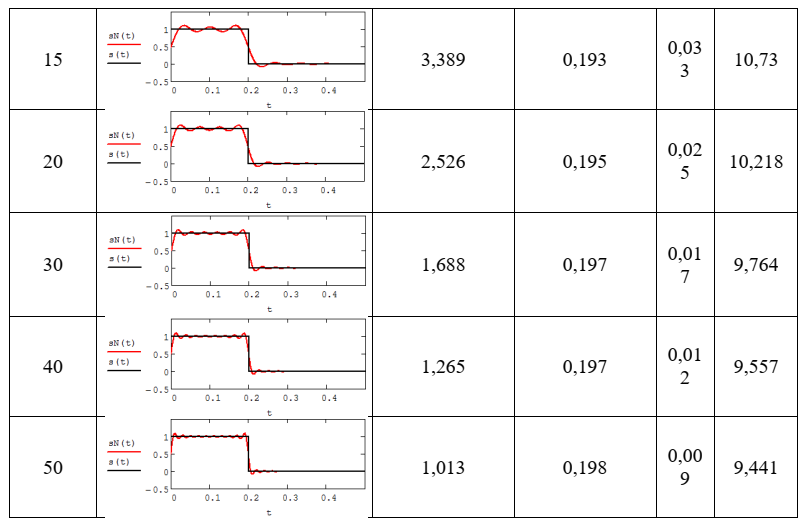 Порядок выполнения работы 1. Запустить Mathcad. 2. Определить в программе Mathcad для заданного периодического сигнала s(t) в соответствии с вариантом индивидуального задания (таблица 2.3): - 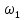 – основную круговую частоту периодического сигнала (частоту первой гармоники), рад/с; – основную круговую частоту периодического сигнала (частоту первой гармоники), рад/с;- 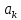 – коэффициент k-й «косинусной» составляющей спектра Фурье периодического сигнала, В; – коэффициент k-й «косинусной» составляющей спектра Фурье периодического сигнала, В;- 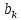 – коэффициент k-й «синусной» составляющей спектра Фурье периодического сигнала, В; – коэффициент k-й «синусной» составляющей спектра Фурье периодического сигнала, В;- 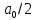 – постоянную составляющую спектра Фурье периодического сигнала, В; – постоянную составляющую спектра Фурье периодического сигнала, В;- 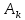 – амплитуду k-й гармоники спектра Фурье периодического сигнала, В; – амплитуду k-й гармоники спектра Фурье периодического сигнала, В;- 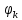 – начальную фазу k-й гармоники спектра Фурье периодического сигнала, радианы или градусы; – начальную фазу k-й гармоники спектра Фурье периодического сигнала, радианы или градусы;- амплитудную и фазовую спектральные диаграммы периодического сигнала (построить линейчатые спектра); - восстановленный по усеченному ряду Фурье сигнал 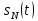 являющийся приближенным изображением сигнала s(t); являющийся приближенным изображением сигнала s(t);- расстояние и квадрат расстояния между сигналами 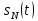 и s(t) за период колебаний T, выраженный в процентной мере относительно квадрата нормы сигнала s(t ); и s(t) за период колебаний T, выраженный в процентной мере относительно квадрата нормы сигнала s(t );- среднюю мощность сигнала s(t) за период колебаний T; - сумму мощностей постоянной составляющей и гармоник спектра Фурье и проверить выполнение неравенства Парсеваля; - tm – момент времени, когда восстановленный по усеченному ряду Фурье сигнал  принимает максимальное значение (исследование эффекта Гиббса); принимает максимальное значение (исследование эффекта Гиббса);- Δ – максимальное значение абсолютной ошибки восстановления сигнала, обусловленное наличием эффекта Гиббса; - Δ% – максимальное значение относительной ошибки восстановления сигнала, обусловленное наличием эффекта Гиббса; 3. Исследовать влияние изменения количества гармоник спектра Фурье сигнала на качество восстановления по усеченному ряду Фурье сигнала  , выполнение неравенства Парсеваля и параметры эффекта Гиббса сигнала , выполнение неравенства Парсеваля и параметры эффекта Гиббса сигнала  . Результаты исследования оформить в виде таблицы 2.2. . Результаты исследования оформить в виде таблицы 2.2.4. Сохранить результаты спектрального анализа и синтеза заданного периодического сигнала. 5. Сформировать отчет по лабораторной работе. 6. Защитить работу. Варианты заданий Номер варианта соответствует номеру фамилии студента в списке учебной группы (подгруппы).  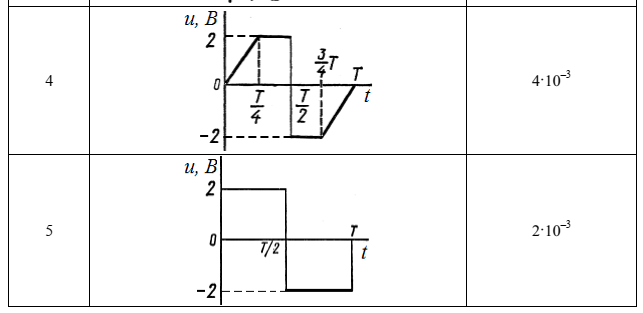 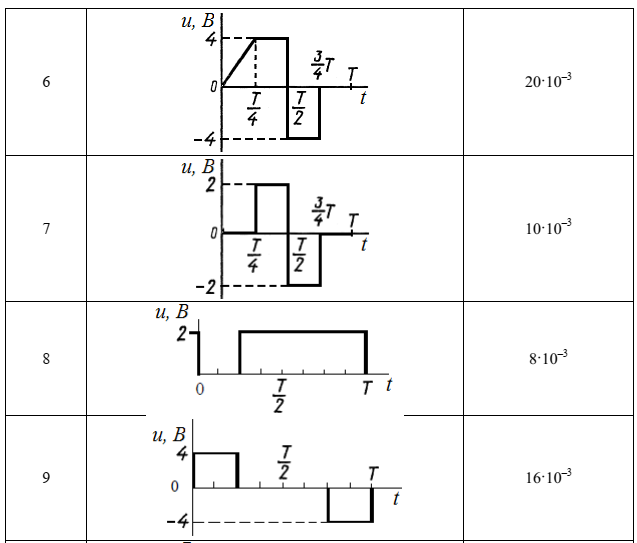 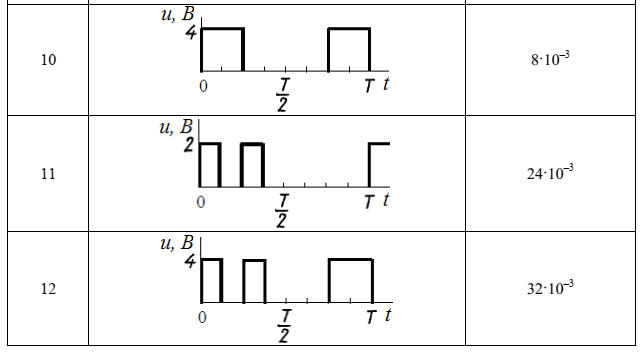 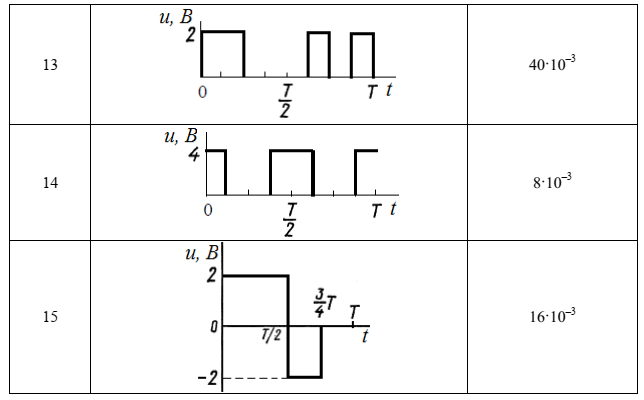 Содержание отчета Отчет по лабораторной работе оформляется в виде документа Word и должен включать: - название лабораторной работы; - цель и программу лабораторной работы; - формулировку индивидуального задания и результат его выполнения; - краткие выводы по результатам выполнения лабораторной работы. Контрольные вопросы 1. Какой сигнал называется периодическим? 2. В чем заключается основная идея спектрального анализа периодических сигналов? 3. Что такое спектр периодического сигнала? 4. Каким требованиям должна удовлетворять периодическая функция времени s(t) для того, чтобы её можно было подвергнуть спектральному анализу по Фурье? 5. Что такое период периодического сигнала? 6. Что такое основная частота периодического сигнала? 7. Как выглядит запись ряда Фурье для периодических сигналов s(t) на интервале времени t (синусно-косинусная, вещественная и комплексная форма)? 8. Каковы базисные функции синусно-косинусной формы ряда Фурье? 9. Как определить постоянную составляющую спектра Фурье периодического сигнала? Каков смысл этого параметра? 10. Как определить коэффициент k-й «косинусной» («синусной») составляющей спектра Фурье периодического сигнала? 11. Какие выводы можно сделать из сравнения между собой вещественной к синусно - косинусной формы записи ряда Фурье? 12. Что такое амплитудный спектр периодического сигнала? 13. Что такое амплитудная спектральная диаграмма периодического сигнала? 14. Что такое фазовый спектр периодического сигнала? 15. Что такое фазовая спектральная диаграмма периодического сигнала? 16. Что такое гармоника? 17. Продолжите фразу: «Если анализируемый сигнал s(t) является вещественным, то ...». 18. Каковы основные свойства спектральных диаграмм периодических сигналов? 19. Продолжите фразу: «Когда возникает необходимость аппроксимировать периодическую функцию тригонометрическим полиномом, то наименьшее квадратичное отклонение получится, если ...». 20. Как формулируется равенство Парсеваля? 21. Что называется спектром мощности периодического сигнала? 22. Чем обусловлен эффект Гиббса при спектральном синтезе периодических сигналов? Как проявляется этот эффект? 23. Какие параметры эффекта Гиббса сигнала были исследованы в лабораторной работе? 24. Какова методика выполнения индивидуального задания? 25. Какие выводы можно сделать по результатам выполнения индивидуального задания? |
